Како пронаћи висину трапеза: формула за све прилике
Постоји неколико одговора на једноставно питање “Како пронаћи висину трапеза?”, Све зато што се могу дати различите почетне вриједности. Према томе, формуле ће варирати.
Ове формуле се могу запамтити, али су лако изведене. Потребно је само примијенити претходно изучене теореме.
Прихвата се у формулама
У свим математичким записима испод, таква читања слова су тачна.
| произвољна трапеза | исосцелес трапезиум | име |
| а | а | боттом басе |
| у | у | топ басе |
| ц, д | са | стране |
| н | н | висина |
| м | м | миддле лине |
| д 1 д 2 | д 1 | дијагонале |
| с | с | квадрат |
| α, β | α | доњи доњи углови |
| γ, δ | γ, δ | углови на пресеку дијагонала |
У изворним подацима: све стране
Да бисте пронашли висину трапеза у општем случају, треба да користите следећу формулу:
н = √ (ц 2 - (((а - ц) 2 + ц 2 - д 2 ) / (2 (а - ц))) 2 ). Број 1.
Не најкраћи, али је у задацима прилично риједак. Обично можете користити друге податке.
Формула која вам говори како пронаћи висину једнакокрачног трапеза у истој ситуацији је много краћа:
н = √ (ц 2 - (а - ц) 2/4). Број 2
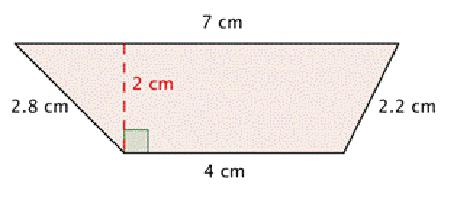
У задатку су дате: стране и углови на дну базе
Претпоставља се да је угао α суседан страни са ознаком "ц", односно, угао β према страни д. Тада ће формула за проналажење висине трапеза уопште бити:
н = ц * син α = д * син β. Број 3
Ако је број једнакокрачан, можете користити ову опцију:
н = ц * син α = ((а - ц) / 2) * тг α. Број 4
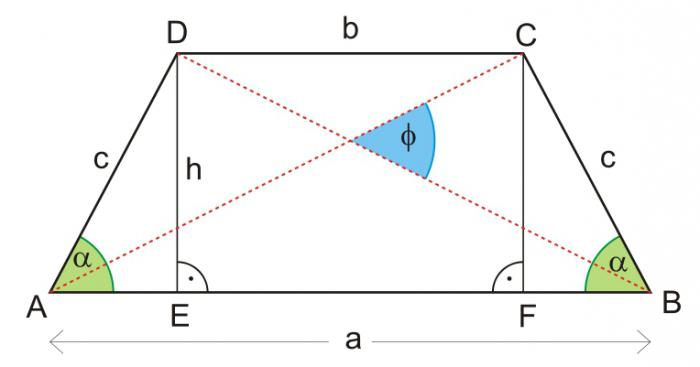
Познати: дијагонале и углови између њих
Типично, овим подацима придружују се још увек познате вредности. На пример, базна или средња линија. Ако се дају основе, онда је одговор на питање како пронаћи висину трапеза користан у следећој формули:
н = (д 1 * д 2 * син γ) / (а + б) или н = (д 1 * д 2 * син δ) / (а + б). Број 5.
Ово је за укупан изглед слике. Ако је дат изосцен, онда ће се запис трансформисати на следећи начин:
н = (д 1 2 * син γ) / (а + б) или н = (д 1 2 * син δ) / (а + б). Број 6.
Када се проблем бави централном линијом трапеза, формуле за проналажење њене висине постају следеће:
н = (д 1 * д 2 * син γ) / 2м или н = (д 1 * д 2 * син δ) / 2м. Соба 5а.
н = (д 1 2 * син γ) / 2м или н = (д 1 2 * син δ) / 2м. Број 6а.
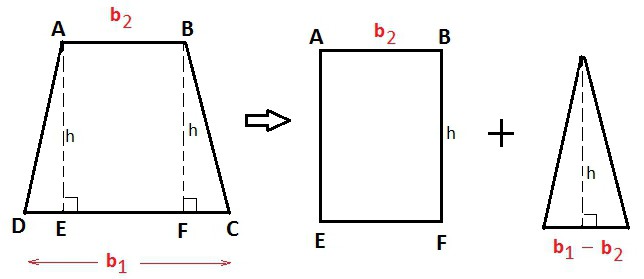
Међу познатим вредностима: подручје са базама или средњом линијом
Ово су можда најкраће и најједноставније формуле за проналажење висине трапеза. За произвољан облик, то ће бити:
н = 2С / (а + ц). Број 7.
То је исто, али са добро познатом средњом линијом:
н = с / м. Соба 7а.
Чудно, али за једнакокрачан трапезоид, формуле ће изгледати исто.
Задаци
№1. О дефиницији углова на дну трапеза.
Цондитион Даје се једнакокрачан трапез, чија је страна 5 цм, а његове базе су 6 и 12 цм, а потребно је пронаћи синус акутног угла.
Одлука. За практичност, потребно је да унесете нотацију. Нека доњи леви врх буде А, све остало у смеру казаљке на сату: Б, Ц, Д. Дакле, доња база ће бити означена као ХЕЛЛ, горња база ће бити БЦ.
Потребно је исцртати висине од врхова Б и Ц. Тачке које означавају крајеве висина биће означене као Х1 и Х2. Пошто су на слици БЦХ 1 Х 2 сви углови равни, то је правоугаоник. То значи да је сегмент Х1Х2 6 цм.
Сада треба да размотримо два троугла. Једнаки су зато што су правоугаони са идентичним хипотенузама и вертикалним ногама. Из тога следи да су њихове мање ноге једнаке. Према томе, они се могу дефинисати као квоцијент разлике. Ово последње се добија одузимањем од доње базе горње. То ће бити подељено са 2. То значи да 12 - 6 мора бити подељено са 2. АН 1 = Х 2 Д = 3 (цм).
Сада из Питхагореанове теореме требате пронаћи висину трапеза. Неопходно је пронаћи синус угла. БХ 1 = √ (5 2 - 3 2 ) = 4 (цм).
Користећи знање о томе како синус акутног угла лежи у правоугаоном троуглу, можемо написати следећи израз: син α = БХ 1 / АБ = 0.8.
Одговор је. Жељени синус је 0.8.
№2. Пронаћи висину трапеза по чувеном тангенту.
Цондитион За једнакокрачан трапезоид, морате израчунати висину. Познато је да су његове основе 15 и 28 цм тангента акутног угла: 11/13.
Одлука. Означавање врхова је исто као у претходном задатку. Опет, морате да држите две висине из горњих углова. По аналогији са решењем првог проблема, потребно је пронаћи АХ 1 = Х 2 Д, који су дефинисани као разлика 28 и 15 подељена са два. Након израчунавања испада: 6,5 цм.
Пошто је тангента однос двају ногу, можемо написати следећу једнакост: тг α = АХ 1 / БХ 1 . Штавише, овај однос је 11/13 (по стању). Пошто је АН 1 познат, могуће је израчунати висину: ВН 1 = (11 * 6.5) / 13. Једноставни израчуни дају резултат од 5.5 цм.
Одговор је. Потребна висина је 5,5 цм.
№3. За израчунавање висине познатих дијагонала.
Цондитион Познато је о трапезу да су његове дијагонале 13 и 3 цм, а потребно је знати његову висину ако је збир база 14 цм.
Одлука. Нека ознака фигуре буде иста као и раније. Претпоставимо да је звучник мања дијагонала. Из врха Ц треба да држите жељену висину и означите је ЦХ.
Сада је потребно извршити додатну изградњу. Из угла Ц, морате нацртати правац паралелан већој дијагонали и наћи тачку његовог пресека са наставком стране крвног притиска. То ће бити Д 1 . Испало је нови трапезоид, унутар којег је нацртан трокут АСД 1 . То је такође неопходно за даље решавање проблема.
Жељена висина ће такође бити у троуглу. Према томе, можете користити формуле проучене у другој теми. Висина троугла је дефинисана као производ броја 2 и површина подељена са стране на коју је нацртана. А страна је једнака суми база оригиналног трапеза. Ово се заснива на правилу да је извршена додатна изградња.
У троуглу који се разматра, све стране су познате. За практичност, уносимо ознаку к = 3 цм, и = 13 цм, з = 14 цм.
Сада можете пребројити подручје, користећи теорему Героне. Полу-периметар ће бити п = (к + и + з) / 2 = (3 + 13 + 14) / 2 = 15 (цм). Тада ће формула за област након замене вредности изгледати овако: С = √ (15 * (15 - 3) * (15 - 13) * (15 - 14)) = 6 (10 (цм2).
Сада треба да бројите висину: н = (2 * 6 √ 10) / 14 = 6√10 / 7 (цм).
Одговор је. Висина је 6√10 / 7 цм.
№4. Тражити висину са стране.
Цондитион Дати трапез, три стране од којих су 10 цм, а четврта 24 цм, морате знати његову висину.
Одлука. Пошто је број једнакокрачан, онда ће вам требати формула број 2. У њој само требате замијенити све вриједности и рачунати. Изгледаће овако:
н = √ (10 2 - (10 - 24) 2/4) = (51 (цм).
Одговор је. н = цм51 цм