Како пронаћи квадратни коријен? Својства, примери екстракције корена

Математика је настала када је особа схватила себе и почела се позиционирати као аутономна јединица свијета. Жеља да се измери, упореди, израчуна оно што те окружује - то је била основа једне од фундаменталних наука наших дана. У почетку, то су били делови елементарне математике, што нам је омогућило да повежемо бројеве са њиховим физичким изразима, каснији закључци су представљени само теоретски (на основу њихове апстрактности), па, након неког времена, како је један научник рекао, "математика је достигла горњу границу сложености када је нестала" све бројеве. " Појам "квадратног коријена" појавио се у вријеме када је лако могао бити подржан емпиријским подацима, који су ишли даље од равнине рачунања.

Како је све почело

Први спомен коријена, који је тренутно означен као √, забиљежен је у списима вавилонских математичара, који су иницирали модерну аритметику. Наравно, изгледали су помало као садашњи облик - научници тих година су прво користили гломазне таблете. Али у другом миленијуму пре нове ере. е. они су извели приближну прорачунску формулу која је показала како извадити квадратни корен. На слици испод је камен на којем су вавилонски научници изрезали процес ,2, и испоставило се да је тако истинито да је разлика у одговору пронађена само на десетом децималном месту.

Осим тога, коријен је коришћен ако је било потребно пронаћи страну трокута, под увјетом да су друга два позната. Па, када одлучујете квадратне једначине Од вађења коријена не може нигдје ићи.

Заједно са вавилонским радовима, предмет чланка је такође проучаван у кинеском раду "Математика у девет књига", а стари Грци су дошли до закључка да било који број из којег се не извлачи корен без остатка даје ирационалан резултат.

Порекло овог термина повезано је са арапским приказом броја: древни научници су веровали да квадрат произвољног броја расте из корена, као биљка. На латинском, ова ријеч звучи као радик (можете пратити узорак - све што има корен значи оптерећење је сугласно, било да је то ротквица или радикулитис).

Научници следеће генерације су прихватили ову идеју, назвавши је Рк. На пример, у КСВ веку, да би указали да је квадратни корен издвојен из произвољног броја а, написали су Р2а. Познато „крпељ“ појавило се тек у 17. стољећу захваљујући Ренеу Десцартесу.

Наши дани

Са становишта математике, квадратни корен и је такав број з, чији је квадрат једнак и. Другим речима, з ² = и је еквивалентно =и = з. Међутим, ова дефиниција је релевантна само за аритметички коријен, јер имплицира не-негативну вриједност израза. Другим речима, =и = з, где је з већи или једнак 0.

Уопштено, оно што функционише да би се дефинисао алгебарски корен, вредност израза може бити и позитивна и негативна. Дакле, због чињенице да з ² = и и (-з) ² = и, имамо: =и = ± з или =и = | з |.

Због чињенице да се љубав према математици са развојем науке само повећала, постоје различите манифестације наклоности према њој, које се не изражавају у сувом рачунању. На пример, у пару са таквим забавним феноменима као што је дан Пи, празнује се и празник квадратног корена. Означавају се девет пута у стотинама година и одређују се по следећем принципу: бројеви, који означавају дан и месец по реду, морају бити квадратни корен године. Дакле, следећи пут морамо да прославимо овај празник 4. априла 2016. године.

Својства квадратног корена на пољу Р

1. Квадратни корен производа једнак је производу квадратног корена, под условом да су радикални изрази већи или једнаки 0.
2. Приликом подизања квадратног корена, довољно је да се на ову снагу подигне радикални израз, под условом да је већи од нуле.
3. Квадратни корен фракције једнак је корену нумератора подељен кореном имениоца, под условом да је квадратни корен нумератора већи или једнак 0, а квадратни корен имениоца је строго већи од 0.
4. Радикални израз, ако је већи од нуле, може се поделити на неколико делова, од којих је, заузврат, дозвољено издвајање корена. На пример: =75 = *25 * 3 = 5√3.
5. Под знаком коријена, можете унијети било који број, док га подижете на квадрат. На пример: 5√8 = *25 * =8 = .200.

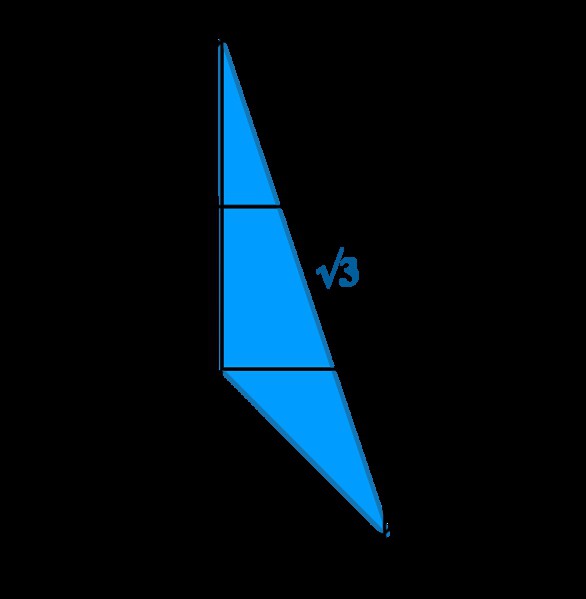
Практично сви математички изрази имају геометријску основу испод њих, ова судбина и ,и, која је дефинисана као страна квадрата са површином и, није побегла.

Како пронаћи корен броја?

Постоји неколико алгоритама за рачунање. Најједноставнији, али прилично тежак, је уобичајени аритметички прорачун, који се састоји од следећег:

1) из броја чијег коријена нам је потребно одузети редом одд бројеви - док излазна биланца није мања од одбитне, или чак нула. Број потеза и на крају ће бити жељени број. На пример, израчунавање квадратног корена од 25:

25-1 = 24

24-3 = 21

21-5 = 17

17-7 = 10

10-9 = 1

Следећи непаран број је 11, остало је следеће: 1 <11. Број потеза је 5, тако да је корен од 25 је 5. Све изгледа лако и једноставно, али замислите шта треба да израчунате из 18769? 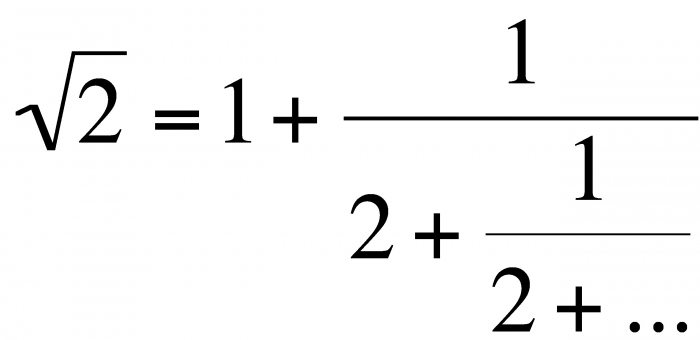За такве случајеве постоји декомпозиција у Таилоровом низу:

√ (1 + и) = ∑ ((- 1) ^н (2н)! / (1-2н) (н!) ² (4 ^н )) и ^н , где н има вредности од 0 до

+ ∞, и | и | ≤1.

Графички приказ функције з = .и

Размотримо елементарну функцију з = √и на пољу реалних бројева Р, где је и већи или једнак нули. Њен распоред је следећи: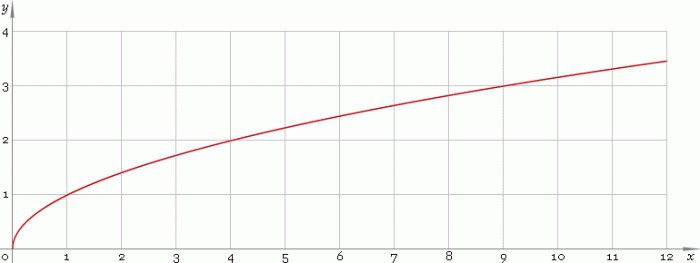

Крива расте од извора и нужно прелази тачку (1; 1).

Својства функције з = они на пољу реалних бројева Р

1. Домена разматране функције је интервал од нуле до плус бесконачности (нула је укључена).

2. Опсег вредности функције која је у питању је интервал од нуле до плус бесконачности (нула је поново укључена).

3. Минимална вредност (0) функције узима само у тачки (0; 0). Недостаје максимална вредност.

4. Функција з = иси није ни парна ни непарна.

5. Функција з = иси није периодична.

6. Тачка пресека графа функције з = √и са осима координата је само једна: (0; 0).

7. Тачка пресека графа функције з = иси је и нула ове функције.

8. Функција з = цонтинуоуслии континуирано расте.

9. Функција з = такеси узима само позитивне вриједности, стога њен граф заузима први координатни кут.

Варијанте функције слике з = .и

У математици, да би се олакшало рачунање сложених израза, понекад се користи облик моћи за писање квадратног корена: =и = и ^1/2 . Таква опција је погодна, на пример, у подизању функције на снагу: ()и) ⁴ = (и ^1/2 ) ⁴ = и ² . Ова метода је такође добра идеја за диференцијацију са интеграцијом, јер је због тога квадратни корен представљен обичном енергетском функцијом.

А у програмирању, замена знака √ је комбинација слова скрт. 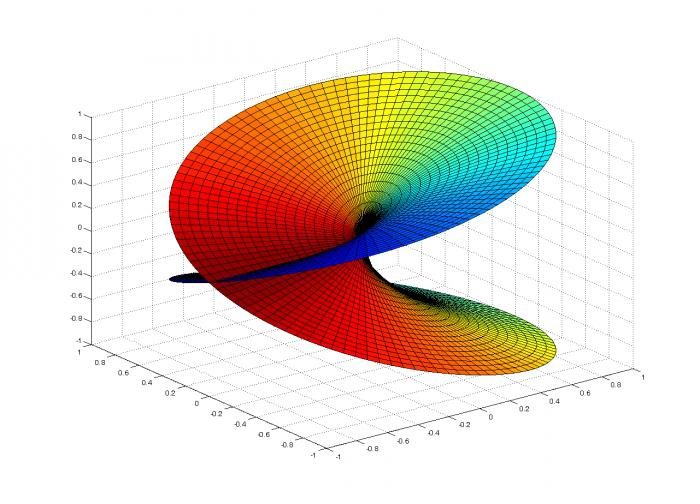Треба напоменути да је у овом подручју квадратни коријен веома тражен, јер је дио већине геометријских формула потребних за прорачуне. Сам алгоритам бројања је прилично сложен и изграђен је на рекурзији (функцији која себе назива).

Квадратни корен у комплексном пољу Ц

Све у свему, то је био предмет овог чланка који је стимулисао отварање поља. комплексни бројеви Ц, будући да математичари нису били опуштени са питањем добијања корена једнаког степена од негативног броја. Тако се појавила имагинарна јединица, коју карактерише веома интересантно својство: његов квадрат је -1. Захваљујући томе, добијене су квадратне једначине и са негативним дискриминантом. У Ц, за квадратни корен, иста својства као у Р су релевантна, једина ствар је да су ограничења на радикалима уклоњена.