Како правилно смањити фракције?

Фракције и њихово смањење - још једна тема која почиње у 5. разреду. Овде се формира основа ове акције, а онда се ове вештине вуку концем у вишу математику. Ако ученик није научио, како смањити фракције онда он може имати проблема у алгебри. Зато је боље разумјети неколико правила једном заувијек. И запамтите једну забрану и никада је не кршите.

Фракција и њено смањење

Шта је то, сваки студент зна. Све две цифре између хоризонталне траке одмах се виде као фракција. Међутим, нису сви разумели да то може бити било који број. Ако је цео број, онда се увек може поделити са једним, онда ћемо добити погрешна фракција. Али о томе касније.

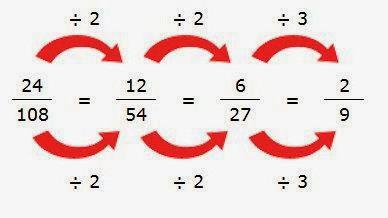
Почетак је увек једноставан. Прво морате да схватите како да смањите тачну фракцију. То јест, онај чији је нумератор мањи од имениоца. За ово треба да запамтите главно својство фракције. Она тврди да множењем (као и подјелом) нумератора и имениоца са истим бројем у исто вријеме, она је еквивалентна оригиналној фракцији.

Део акција које се обављају у овој имовини и доводе до смањења. То јест, његово максимално поједностављење. Фракција се може смањити све док постоје заједнички фактори изнад и испод линије. Када их нема, смањење је немогуће. И кажу да је ова фракција несводива.

Два пута

1. Смањење корак по корак. Она користи метод процене, када су оба броја подељена са минималним заједничким фактором који је студент приметио. Ако се након прве контракције види да то није крај, онда се подјела наставља. Док фракција не постане несводива.

2. Проналажење највећег заједничког делиоца нумератора и имениоца. Ово је најрационалнији начин за смањење фракција. То подразумева декомпозицију нумератора и имениоца у основне факторе. Међу њима, онда морате одабрати све исто. Њихов производ ће дати највећи заједнички фактор, који је смањена фракција.

Обе ове методе су еквивалентне. Студент је позван да их савлада и користи онај који им се највише допао.

Шта ако постоје слова и акције збрајања и одузимања?

Први део питања је мање-више јасан. Слова се могу скратити као бројеви. Главно је да они дјелују као мултипликатори. Али са другим, многи имају проблема.

Важно је запамтити! Можете смањити само бројеве који су множитељи. Ако су услови, то је немогуће.

Да бисте разумели како смањити фракције које имају облик алгебарског израза, морате научити правило. Прво представите бројник и именитељ у облику дјела. Тада можете смањити, ако постоје заједнички фактори. За представљање у облику мултипликатора, корисне су следеће технике:

• групирање;
• наметање заграда;
• примена идентитета скраћеног множења.

Штавише, овај други метод омогућава да се термини одмах добију у облику мултипликатора. Због тога се мора увек користити ако је видљив познати образац.

Али то није страшно, онда се појављују задаци са степенима и коренима. Тада вам је потребна храброст и научите неколико нових правила.

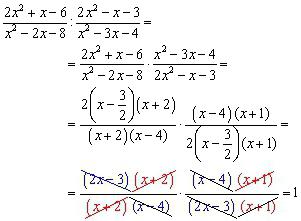
Израз са степеном

Фрацтион У производу нумератора и имениоца. Постоје слова и бројеви. И они су подигнути на моћ, која се такође састоји од термина или фактора. Постоји нешто чега се треба бојати.

Да бисте схватили како смањити фракције са степенима, морате научити две ствари:

• ако је експоненат сума, онда се може проширити на факторе, чији ће степени бити оригинални термини;
• ако је разлика дељива и дељива, прва ће имати смањење степена, а друга ће имати одбитак.

Након обављања ових радњи постају видљиви заједнички фактори. У таквим примјерима није потребно израчунавати све ступњеве. Довољно је само смањити степене са истим показатељима и основама.

Да бисте коначно сазнали како смањити фракције са степенима, морате много вежбати. Након неколико примера истог типа, акције ће се извршити аутоматски.

А ако је израз корен?

Такође се може смањити. Али опет, поштујући правила. И сви они који су горе описани су истинити. Уопштено, ако постоји питање о томе како смањити фракцију са коријенима, онда морате подијелити.

Ирационални изрази се такође могу поделити. То јест, ако су бројник и именилац идентични фактори затворени под знаком корена, онда се они могу сигурно смањити. Ово ће поједноставити израз и извршити задатак.

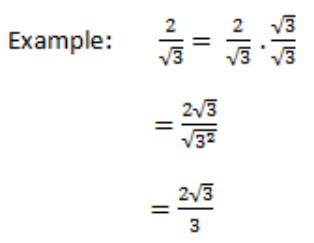
Ако, након редукције испод линије фракција, ирационалност остане, онда она мора бити елиминисана. Другим речима, помножите бројник и именилац. Ако након ове операције постоје заједнички фактори, морат ће се поново смањити.

Овде, можда, све о томе како смањити фракције. Постоји неколико правила, али једна забрана. Никада немој скратити рокове!