Неисправне фракције: како научити решавати примере са њима?

Када је реч "фракције" трче многи. Јер се сећам школе и задатака које сам одлучио о математици. То је била одговорност која је морала бити испуњена. А шта ако се задаци који садрже исправне и нетачне фракције третирају као слагалицу? На крају крајева, многи одрасли рјешавају дигиталне и јапанске крижаљке. Разумите правила и све. Тако да је овде. Треба само схватити теорију - и све ће пасти на своје мјесто. А примери ће се претворити у начин да се тренира мозак.

Које врсте фракција постоје?

За почетак, шта је то. Фракција је број који има један део. Може се писати у два облика. Прва се зове обична. То јест, онај који има хоризонталну или косу црту. То је једнако знаку поделе.

У таквом запису, број изнад цртице се зове нумератор, а испод њега именилац.

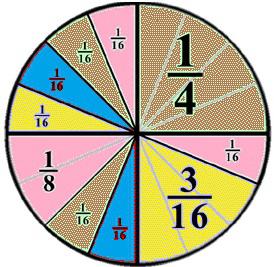
Међу обичним додељују се и правилне и неправилне фракције. У првом, нумератор по модулу је увек мањи од имениоца. Зато се називају погрешним, јер имају све супротно. Вредност тачне фракције је увек мања од једне. Иако је погрешно увек веће од овог броја.

Још увек постоје мешовити бројеви, тј. Они који имају целобројне и делове делова.

Друга врста записа је децимална. О њој посебан разговор.

Која је разлика између неправилних фракција и мешаних бројева?

У основи, ништа. То је само другачији запис истог броја. Неисправне фракције након једноставних поступака лако постају мјешовите. И обрнуто.

Све зависи од конкретне ситуације. Понекад је у задацима прикладније користити неисправну фракцију. А понекад је потребно превести га у мјешовити број и онда ће се примјер врло лако ријешити. Дакле, шта користити: неисправне фракције, мјешовити бројеви - овиси о проматрању рјешавања проблема.

Мјешовити број се такође пореди са сумом целог дела и фракцијским. Други је увек мањи од једног.

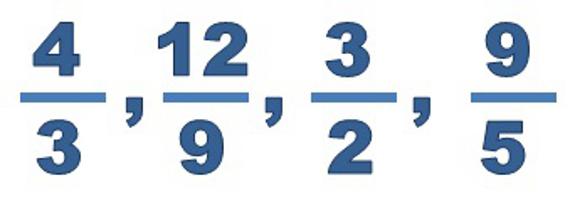
Како представити мјешовити број у облику неправилне фракције?

Ако желите да извршите радњу са неколико бројева који су снимљени у различитим формама, онда их морате учинити истим. Један од начина је представљање бројева као неправилних фракција.

У ту сврху морате извршити радње према овом алгоритму:

• помножите именилац са целим бројем;
• додати резултат резултату нумератора;
• напиши одговор изнад линије;
• деноминатор остаје исти.

Ево примера како написати нетачне делове мешаних бројева:

• 17 (= (17 к 4 + 1): 4 = 69/4;
• 39 ½ = (39 к 2 + 1): 2 = 79/2.

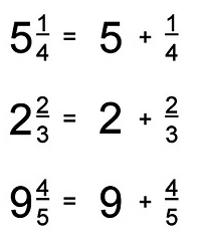
Како написати неприкладну фракцију у облику мјешовитог броја?

Следећа техника је супротна од горе наведених. То јест, када су сви мјешовити бројеви замијењени неправилним фракцијама. Алгоритам акција ће бити следећи:

• поделити бројник имениоцем док се не добије равнотежа;
• написати количник на месту целог дела мешовитог;
• остатак треба ставити изнад линије;
• делилац ће бити именилац.

Примери такве трансформације:

76/14; 76:14 = 5 са ​​остатком од 6; одговор је 5 целих бројева и 6/14; фракциони део у овом примеру треба да се смањи за 2, биће 3/7; коначни одговор је 5 3/7.

108/54; након поделе, парцијал 2 се добија без остатка; То значи да све неправилне фракције не могу бити представљене као мешовити број; одговор је цели број - 2.

Како претворити цијели број у неправилну фракцију?

Постоје ситуације када је таква акција неопходна. Да бисте добили погрешне делове са претходно познатим имениоцем, морате да покренете овај алгоритам:

• помножите цео број са жељеним имениоцем;
• напишите ову вредност изнад линије;
• именилац места испод њега.

Најлакша опција када је именилац један. Онда се ништа не треба умножавати. Довољно је само написати цијели број наведен у примјеру и смјестити јединицу испод линије.

Пример : 5 да направите неправилну фракцију са имениоцем 3. Након множења 5 са ​​3, добијамо 15. Овај број ће бити именилац. Фактор одговора: 15/3.

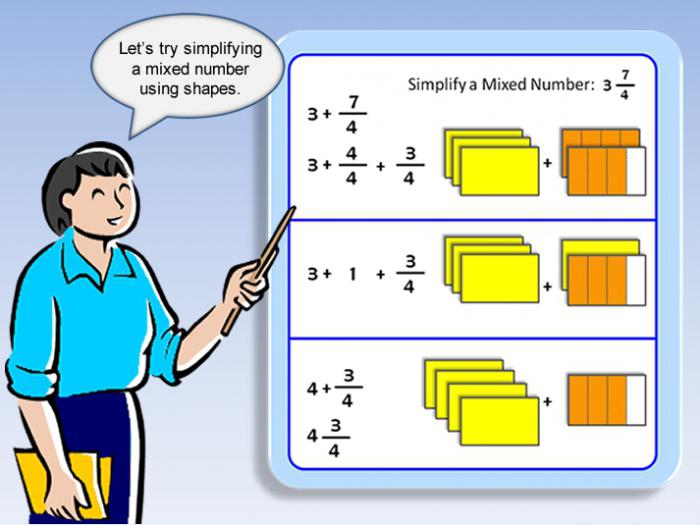
Два приступа рјешавању задатака с различитим бројевима

У примеру је потребно израчунати суму и разлику, као и производ и количник два броја: 2 целих бројева 3/5 и 14/11.

У првом приступу, мјешовити број ће бити представљен као неправилна фракција.

Након извршавања горе описаних корака добијате следећу вредност: 13/5.

Да бисте сазнали износ, морате да доведете фракцију у исти именитељ. 13/5 након множења са 11 ће постати 143/55. 14/11 након множења са 5 има форму: 70/55. Да бисте израчунали износ, потребно је само додати нумераторе: 143 и 70, а затим написати одговор једним имениоцем. 213/55 - овај погрешан дио је одговор на проблем.

Када се нађе разлика, исти бројеви се одузимају: 143 - 70 = 73. Одговор ће бити фракција: 73/55.

Када се множите 13/5 и 14/11 не треба да водите до заједничког именитеља. Довољно је да се у паровима множе нумератори и имениоци. Одговор ће бити: 182/55.

Исто је и са поделом. За исправно рјешење потребно је замијенити дијељење множењем и окренути раздјелник: 13/5: 14/11 = 13/5 к 11/14 = 143/70.

У другом приступу, неправилна фракција се претвара у мешовити број.

После извођења акција, алгоритам 14/11 ће се претворити у мешовити број са целим делом 1 и фракцијским 3/11.

Приликом израчунавања износа потребно је засебно додати цијеле и дјеломичне дијелове. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Коначни одговор је 3 бод 48/55. У првом приступу била је фракција 213/55. Можете проверити исправност тако што ћете га превести у мешовити број. Након што смо поделили 213 на 55, добили смо количник 3 и остатак 48. Лако је видети да је одговор тачан.

Када се одузме, знак "+" се замењује са "-". 2 - 1 = 1, 33/55 - 15/55 = 18/55. Да бисте проверили одговор из претходног приступа, потребно је да преведете у мешовити број: 73 је дељиво са 55 и добијате делимично 1 и остатак 18

Мијешање бројева је незгодно за проналажење посла и количника. Увек се препоручује да идете на погрешне фракције.