Увод у динамичко програмирање

Међу проблемима који се решавају уз помоћ математичког програмирања, можемо издвојити посебну класу проблема која захтева оптимизацију вишестепених (вишестепених) процеса. Такви задаци се разликују по могућности да се решење подели на неколико међусобно повезаних корака. За решавање таквих проблема користи се динамичко програмирање или, како се још назива, вишестепено програмирање. Његове методе су оптимизоване за проналажење оптималног решења вишестепених проблема, који се могу поделити у неколико фаза, корака, итд.

Порекло термина

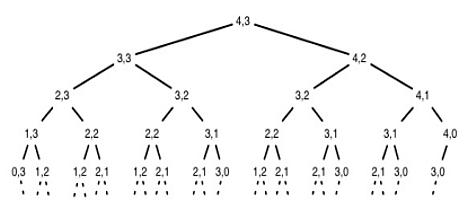
Употреба речи „динамички“ у наслову је првобитно подразумијевала да ће се подјела на подзадатке одвијати углавном у времену. Када се користе динамичке методе за рјешавање производних, пословних и других задатака, у којима је укључен временски фактор, разбијање у одвојене фазе није тешко. Међутим, могуће је користити технику динамичког програмирања у задацима у којима појединачне фазе нису временски повезане. Увијек у вишестепеном задатку, можете одабрати параметар или својство, према којем можете подијелити у засебне кораке.

Алгоритам (метода) за решавање вишестепених проблема

Алгоритам или Метода динамичког програмирања заснива се на принципу секвенцијалне оптимизације проблема, када се рјешење опћег проблема подијели на више рјешења појединачних подзадатака с накнадном интеграцијом у једно рјешење. Врло често, појединачни подзадаци су исти, а једно уобичајено рјешење значајно смањује вријеме израчунавања. 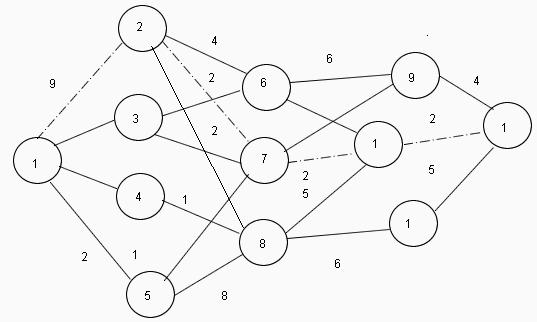Карактеристика методе је аутономија решавања проблема у свакој одвојеној фази, тј., Без обзира на то како је процес оптимизован и решен у претходној фази, тренутни прорачун користи само параметре процеса који га карактеришу у овом тренутку. На пример, возач који вози на путу одлучује о тренутном скретању без обзира на то колико или колико је пре возио.

Метод изнад и метод испод

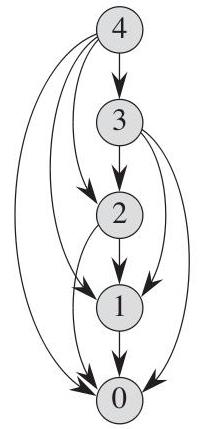
Упркос чињеници да се приликом рачунања у одвојеној фази решавања проблема користе параметри процеса за тренутни тренутак, резултат оптимизације на претходном нивоу утиче на израчунавање наредних фаза како би се постигао најбољи резултат уопште. Динамичко програмирање такав принцип одлучивања назива методом оптималности, која одређује да оптимална стратегија за решавање проблема, без обзира на почетне одлуке и услове, мора да представља оптималну стратегију за почетно стање у наредним фазама. Као што видимо, процес рјешавања проблема је континуирана оптимизација резултата у свакој одвојеној фази од прве до посљедње. Овај метод се зове метода горњег програмирања. На слици је шематски приказан алгоритам решења од врха до дна. Али постоји класа вишестепених проблема у којима је максимални ефекат већ познат у последњој фази, на пример, већ смо стигли из тачке А у тачку Б и сада желимо да знамо да ли смо исправно корачали у свакој претходној фази или да можемо да урадимо нешто оптималније. Појављује се рекурзивна секвенца фаза, тј. Идемо као да је "од супротног". Овај метод решења се назива "метода програмирања на дну".

Практична примена

Динамичко програмирање се може користити у било ком области деловања тамо гдје постоје процеси који могу бити на било којем параметру (вријеме, количина, температура, итд.) подијељени у неколико идентичних малих фаза. Најчешће коришћене динамичке методе решења су добијене у теорији управљања и развоју рачунарских система.

Потражите најбољи пут

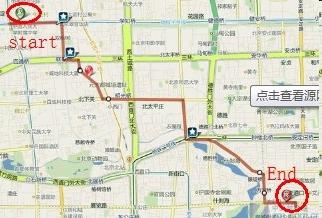
Користећи динамичку оптимизацију, могуће је ријешити широку класу проблема проналажења или оптимизације најкраћег пута и других проблема у којима “класични” начин набрајања могућих рјешења доводи до повећања времена израчунавања, а понекад је опћенито неприхватљиво. Класичан проблем динамичког програмирања је проблем руксака: дат је одређени број објеката са одређеном масом и трошковима, а потребно је изабрати скуп објеката са максималном вриједношћу и масом која не прелази обујам руксака. Класично набрајање свих опција у потрази за оптималним решењем траје доста времена, а уз помоћ динамичких метода проблем се решава у разумном времену. Задаци проналажења најкраћег пута за транспортну логистику су основни, а методе динамичког решења су оптимално погодне за њихово решавање. Најједноставнији примјер таквог задатка је изградња најкраћег пута аутомобилским ГПС навигатором.

Производња

Динамичко програмирање се широко користи у решавању различитих производних задатака, као што је управљање залихама за одржавање потребног броја компоненти у сваком тренутку, планирање производног процеса, одржавање опреме и ремонт, униформно оптерећење особља, најефикаснија алокација инвестиционих фондова, итд. За рјешавање производних проблема кориштењем метода динамичког програмирања развијени су посебни софтверски пакети и Интегрисан у популарне системе за управљање предузећима као што је САП.

Научна област

Методе динамичког програмирања широко се користе у различитим научним истраживањима. На пример, они се успешно користе у алгоритмима за препознавање говора и слике, у обради великих поља података у социологији и економске активности.