Кинетичка енергија - енергија кретања тела
Потенцијална и кинетичка енергија омогућавају нам да окарактеришемо стање сваког тела. Ако се прва користи у системима интеракцијских објеката, онда је она повезана са њиховим кретањем. Ови типови енергије се, по правилу, разматрају када је сила која повезује тела независна од путање кретања. У овом случају, важне су само почетне и завршне позиције.
Опште информације и концепти
Кинетичка енергија система је једна од њених најважнијих карактеристика. Физичари разликују два типа такве енергије у зависности од типа кретања:
• прогресивно;
• ротација.
Кинетичка енергија ( Ек ) је разлика између укупне енергије система и преостале енергије. На основу тога можемо рећи да је то због кретања система. Тело га има само када се креће. У мировању, објекат је нула. Кинетичка енергија било ког тела зависи искључиво од брзине кретања и њихових маса. Укупна енергија система директно зависи од брзине његових објеката и удаљености између њих.
Основне формуле
У случају када било која сила (Ф) дјелује на тијело које је у мировању на такав начин да долази у покрет, можемо говорити о обављању посла дА. Вредност ове енергије дЕ ће бити већа, више посла ће бити обављено. У овом случају, следећа једнакост је истинита: дА = дЕ.
С обзиром на путању тијела (дР) и његове брзине (дУ), можете користити 2 Невтонов закон, на основу којег: Ф = (дУ / дЕ) * м.
Наведени закон се користи само када постоји инерцијални референтни систем. Постоји још једна важна нијанса која се узима у обзир у прорачунима. На вредност енергије утиче избор система. Према СИ систему, он се мери у џулима (Ј). Кинетичку енергију тела карактерише маса м, као и брзина кретања υ. У овом случају то ће бити: Е к = ((υ * υ) * м) / 2.
На основу горње формуле можемо закључити да је кинетичка енергија одређена масом и брзином. Другим речима, то је функција покрета тела.
Енергија у механичком систему
 Кинетичка енергија је механичка енергија систем. То зависи од брзине његових тачака. Свака енергија материјална тачка је представљена следећом формулом: Е = 1 / 2мυ 2, где је м маса тачке, а υ њена брзина.
Кинетичка енергија је механичка енергија систем. То зависи од брзине његових тачака. Свака енергија материјална тачка је представљена следећом формулом: Е = 1 / 2мυ 2, где је м маса тачке, а υ њена брзина.
Кинетичка енергија механичког система је аритметичка сума истих енергија свих њених тачака. Такође се може изразити следећом формулом: Е к = 1 / 2Мυ ц2 + Ец, где је υц брзина центра масе, М маса система, Ец је кинетичка енергија система када се креће око центра масе.
Солид енерги
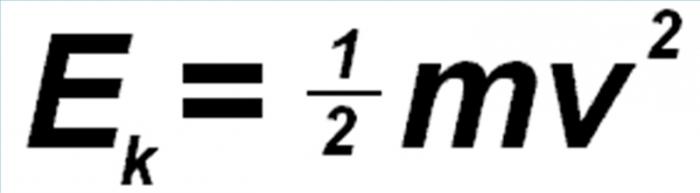 Кинетичка енергија тела, која се креће прогресивно, одређена је истом енергијом тачке са масом која је једнака маси целог тела. За израчунавање индикатора приликом кретања примјењују се сложеније формуле. Промена ове енергије система у тренутку њеног кретања из једног положаја у друго јавља се под утицајем примењених унутрашњих и спољашњих сила. Она је једнака суми рада Ауе и А'у ових сила током овог кретања: Е2 - Е1 = Ау Ауе + Ау А'у.
Кинетичка енергија тела, која се креће прогресивно, одређена је истом енергијом тачке са масом која је једнака маси целог тела. За израчунавање индикатора приликом кретања примјењују се сложеније формуле. Промена ове енергије система у тренутку њеног кретања из једног положаја у друго јавља се под утицајем примењених унутрашњих и спољашњих сила. Она је једнака суми рада Ауе и А'у ових сила током овог кретања: Е2 - Е1 = Ау Ауе + Ау А'у.
Ова једнакост одражава теорему о промени кинетичке енергије. Уз његову помоћ решавају се најразличитији проблеми механике. Без ове формуле немогуће је ријешити низ важних задатака.
Кинетичка енергија при великим брзинама
Ако је брзина тела близу брзине светлости, кинетичка енергија материјалне тачке може се израчунати следећом формулом:
Е = м0ц2 / -1-υ2 / ц2 - м0ц2,
где је ц брзина светлости у вакууму, м0 је маса тачке, м0ц2 је енергија тачке. На малој брзини (у За време ротације тела око осе, сваки од њених елементарних запремина масе (ми) описује круг радијуса ри. У овом тренутку, запремина има линеарну брзину υи. Зато што се сматра чврста маса, ангулар велоцити ротација свих волумена ће бити иста: ω = υ1 / р1 = υ2 / р2 = ... = υн / рн (1). Кинетичка енергија ротације чврстог материјала је сума свих истих енергија њених елементарних волумена: Е = м1υ1 2/2 + миυи 2/2 + ... + мнυн 2/2 (2). Када користимо израз (1), добијамо формулу: Е = Јз ω 2/2, где је Јз момент инерције тела око З осе. Када се упореде све формуле, постаје јасно да је момент инерције мера инерције тела током ротационо кретање. Формула (2) је погодна за објекте који ротирају око фиксне осе. Кинетичка енергија тијела које се креће низ равнину састоји се од енергије ротације и транслацијског гибања: Е = мυц2 / 2 + Јз ω 2/2, гдје је м маса покретног тијела, Јз је тренутак инерције тијела око оси, υц је брзина центра масе, ω је угаона брзина. Промена вредности кинетичке енергије је уско повезана са потенцијалом. Суштина овог феномена може се разумети кроз закон очувања енергије у систему. Збир Е + дП током кретања тела ће увек бити исти. Промена вредности Е увек се јавља истовремено са променом дП. Тако се оне трансформишу, као да тече једна у другу. Такав феномен може се наћи у готово свим механичким системима. За израчунавање енергетске вредности бира се произвољни моменат (сматра се почетним) и референтни систем. Могуће је одредити тачну количину потенцијалне енергије само у зони утицаја сила које не зависе од путање тела приликом извођења радова. У физици се те силе називају конзервативне. Они имају сталну везу са законом о очувању енергије. Ако је спољни утицај минималан или сведен на нулу, систем који се проучава увек ће бити у стању у коме ће његова потенцијална енергија такође тежити нули. На пример, лопта бачена ће достићи границу те енергије у горњој тачки путање и у истом тренутку ће почети да пада. У овом тренутку, акумулирана енергија у лету претвара се у кретање (рад извршен). За потенцијалну енергију, у сваком случају, постоји интеракција најмање два тела (у примеру са лоптом, гравитација планете утиче на њу). Кинетичка енергија се може израчунати појединачно за свако помично тијело. Потенцијална и кинетичка енергија се мијења искључиво у интеракцији тијела, када сила која дјелује на тијело обавља рад, чија је вриједност различита од нуле. У затвореном систему, рад силе силе или еластичности једнак је промени потенцијалне енергије објеката са знаком "-": А = - (Еп2 - Еп1). Рад силе или еластичности једнак је промени енергије: А = Ек2 - Ек1. Из поређења обе једначине јасно је да је промена енергије објеката у затвореном систему једнака промени потенцијалне енергије и супротна је предзнаку: Ек2 - Ек1 = - (Еп2 - Еп1), или на други начин: Ек1 + Еп1 = Ек2 + Еп2. Из ове једнакости јасно је да сума ових двију енергија тела у затвореном механичком систему и интеракционим силама еластичности и агресије увек остаје константна. На основу горе наведеног, може се закључити да у процесу проучавања механичког система треба размотрити интеракцију потенцијалне и кинетичке енергије. 
Ротациона енергија система
Планарни покрет тела

Промена енергије у механичком систему
Енергетска интерконекција
Потенцијалне и кинетичке енергије су уско повезане. Њихова сума се може представити као укупна енергија система. На молекуларном нивоу је унутрашња енергија тело. Присутна је стално, све док постоји бар нека интеракција између тела и топлотног кретања. Избор референтног система
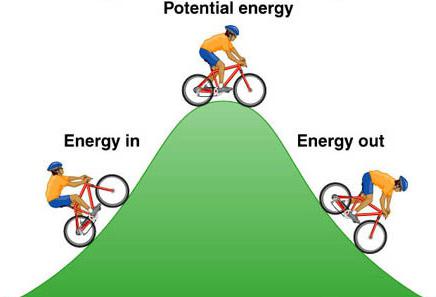
Суштина разлике између потенцијалне и кинетичке енергије
Повезивање различитих енергија