Логаритми: правила, основна својства и формуле

Логаритми и правила акција са њима су прилично пространи и једноставни. Стога, да бисте разумели ову тему, нећете бити тешко. Након што научите сва правила природних логаритама, сваки проблем ће бити ријешен самостално. Прво упознавање са овом темом може изгледати досадно и бесмислено, али је уз помоћ логаритама ријешено много проблема математичара 16. стољећа. "О чему се ради?" - Мислио си. Прочитајте чланак до краја и сазнајте да овај одељак "Царине Сциенцес" може бити од интереса не само за математичаре, научнике егзактних наука, већ и за уобичајене средњошколце.

Дефиниција логаритма

Почнимо са дефиницијом логаритма. Као што многи уџбеници кажу: логаритам броја б на бази а (лог _а б) је одређени број ц за који та једнакост вриједи: б = а ^ц . То је, једноставно речено, логаритам је одређени степен до којег се гради база да би се добио одређени број. Али важно је запамтити да логаритам облика лог _а б има смисла само када: а> 0; а је број који није 1; б> 0, дакле, закључујемо да се логаритам може наћи само за позитивне бројеве.

Класификација логаритама по бази

Логаритми могу бити било који позитивни број у бази. Постоје и два типа: природни и децимални логаритми.

• Природни логаритам - логаритам са базом е (е је Ејлеров број, нумерички приближно једнак 2.7, ирационални број који је уведен за експоненцијалну функцију и = е ^к ) означен је као лн а = лог _е а;
• Децимални логаритам је логаритам са базом 10, то јест, лог ₁₀ а = лг а.

Основна правила логаритама

Прво се морате упознати са основним логаритамским идентитетом: ^{лог _а б} = б, затим слиједите ова два основна правила:

• лог _а 1 = 0 - пошто је било који број у нултом степену 1;
• лог _а а = 1.

Захваљујући открићу логаритма, није нам тешко ријешити апсолутно било коју експоненцијалну једнаџбу, чији се одговор не може изразити природним бројевима, већ само ирационалним. На пример: 5 ^к = 9, к = лог ₅ 9 (пошто за ову једначину нема природног к).

Радње са логаритмима

• лог _а (к · и) = лог _а к + лог _а и - да бисте пронашли логаритам производа, морате додати логаритме фактора. Имајте на уму да су базе логаритама исте. Ако ово напишемо обрнутим редоследом, добијамо правило додавања логаритама.
• лог _а ки = лог _а к - лог _а и - да бисте пронашли логаритам одређеног, потребно је да пронађете разлику између логаритама дивиденде и делиоца. Имајте на уму: логаритми имају исту базу. При писању обрнутим редоследом добијамо правило одузимања логаритама.

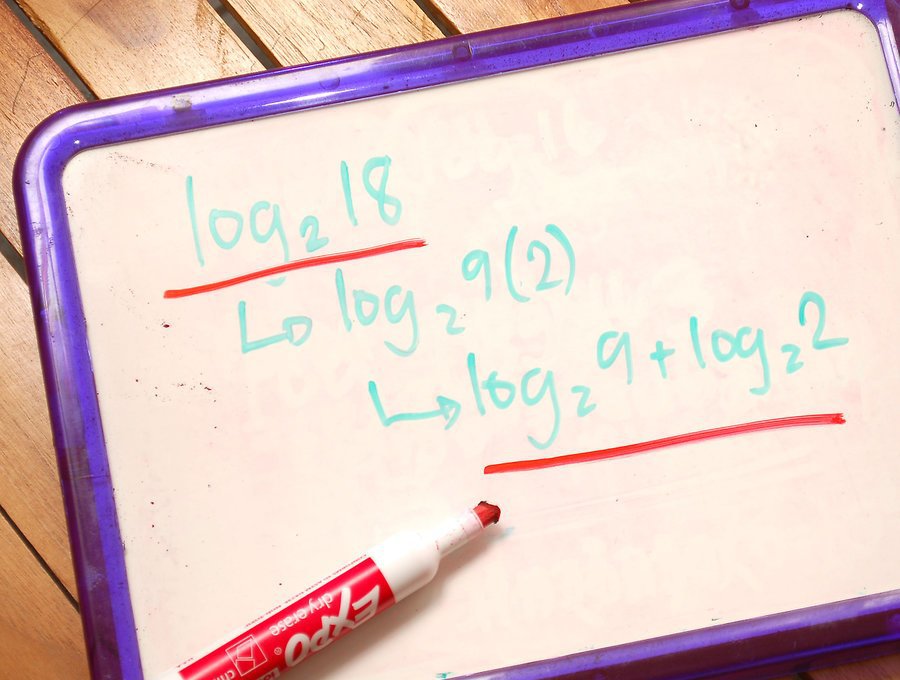
• лог _{а ^к} к ^п = (п / к) * лог _а к - дакле, ако постоје степени у аргументу и база логаритма, онда се могу узети из логаритамског знака.
• лог _а к = лог _{а ^ц} к ^ц је посебан случај претходног правила, када су експоненти једнаки, могу се смањити.
• лог _а к = (лог _б к) (лог _б а) је тзв. транзициони модул, поступак претварања логаритма у другу базу.
• лог _а к = 1 / лог _к а је посебан случај транзиције, промене места базе и датог броја. Читав израз, фигуративно говорећи, окреће се, а логаритам са новом базом појављује се у имениоцу.

Историја логаритама

У КСВИ вијеку постало је неопходно провести многе приближне калкулације за рјешавање практичних проблема, углавном у астрономији (на примјер, одређивање положаја брода од стране Сунца или звијезда).

Ова потреба је убрзано расла и знатне потешкоће створиле су мултипликацију и поделу вишеслојних бројева. Математички математичар Напиер је одлучио да замијени радно интензивно умножавање обичним додатком за тригонометријске израчуне, успоређујући неке прогресије за ово. Тада се подела, на сличан начин, замењује једноставнијом и поузданијом процедуром - одузимањем, а да би се издвојио корен н-тог степена, потребно је поделити логаритам радичног и н. Решење тако тешког задатка у математици јасно је одражавало Напер-ове циљеве у науци. Ево како је о томе писао на почетку своје књиге Рабдологија:

Увек сам се трудио, што се тиче мојих моћи и способности, да ослободим људе од потешкоћа и досаде рачунања, што мучнина обично застрашује многе људе од учења математике.

Име логаритма је предложио сам Напиер, добивен је комбинирањем грчких ријечи, што у комбинацији значи „број односа“.

Основу логаритма је увео Спадел. Позајмио је Еулера из теорије степена и пребацио се у теорију логаритама. Концепт логаритмизма постао је славан захваљујући Коппу у 19. веку. А употреба природних и децималних логаритама, као и њихових ознака, појавила се захваљујући Цауцхију.

Године 1614. Јохн Напиер је на латинском објавио есеј "Опис невероватне таблице логаритама". Било је кратког описа логаритама, правила и њихових својстава. Тако је термин "логаритам" успостављен у егзактним наукама.

Логаритамска операција и прво помињање су се појавили захваљујући Валлису и Јоханну Берноуллију, а коначно га је основао Еулер у КСВИИИ веку.

То је Еулер-ова заслуга у проширењу логаритамске функције форме и = лог _а к на комплексну домену. У првој половини КСВИИИ века објављена је његова књига "Увод у анализу бесконачности", у којој су се појавиле модерне дефиниције експоненцијалних и логаритамских функција.

Логаритамска функција

(имеет смысл, только если: а > 0, а ≠ 1). Функција облика и = лог _а к (има смисла само ако: а> 0 и = 1).

• Логаритамска функција је одређена скупом свих позитивних бројева, јер записни запис _а к постоји само под условом - к> 0;
• Ова функција може узети апсолутно све вриједности из скупа Р (реални бројеви). Пошто сваки реални број б има позитиван к да би задовољио једнакост лог _а к = б, то јест, ова једначина има корен - к = а ^б (следи из чињенице да лог _а а ^б = б).
• Функција се повећава на интервалу а> 0, а смањује на интервалу 0 <а <1.
• Ако је а> 0, онда функција добија позитивне вредности за к> 1.

Треба имати на уму да сваки график логаритамске функције и = лог _и к има једну стационарну тачку (1; 0), јер је лог _и 1 = 0. То се јасно види на слици испод.

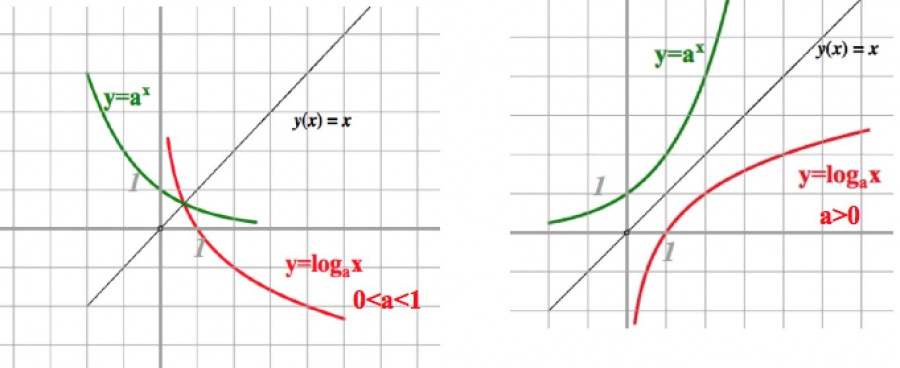
Као што видимо на сликама, функција нема равност или необичност, нема највећих или најмањих вредности, није ограничена одозго или одоздо.

Логаритамска функција и = лог _а к и експоненцијална функција и = а ^к , гдје су (а> 0, и 1) међусобно инверзни. То се може видјети на слици њихових графова.

Решавање проблема са логаритмима

Обично решење проблема који садржи логаритме заснива се на конвертовању у стандардни облик или има за циљ поједностављивање израза под знаком логаритма. Или је потребно превести уобичајене природне бројеве у логаритме са потребном основом, како би се извршиле даље операције како би се поједноставио израз.

Постоје неке суптилности које не треба заборавити:

• Приликом решавања неједнакости, када оба дела стоје испод логаритма према правилу са једном базом, не журите да “одбаците” логаритамски знак. Запамтите монотоније интервала логаритамске функције. Пошто је база већа од 1 (случај када се функција повећава) - знак неједнакости остаје непромијењен, али када је база већа од 0 и мања од 1 (случај када функција опада) - знак неједнакости мијења се у супротно;
• _а х = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. Не заборавите дефиницију логаритма: лог _и к = б, а> 0, и анд 1 и к> 0, како не бисте изгубили корене због нерегистрованог опсега валидних вредности. ТЛД (дозвољени опсег вредности) постоји за скоро све сложене функције.

При решавању логаритамских једначина препоручује се коришћење еквивалентних трансформација. Такође, морате бити пажљиви и узети у обзир могуће трансформације које могу довести до губитка неких коријена.

То су уобичајене, али велике грешке које су многи наишли у потрази за правим одговором за задатак. Не постоји толико много правила за решавање логаритама, тако да је ова тема једноставнија од других и каснијих, али треба добро разумети.

Закључак

Ова тема на први поглед може изгледати компликовано и гломазно, али, истражујући је дубље и дубље, почињете да схватате да се тема управо завршава, а потешкоће не узрокују ништа. Прегледали смо сва својства, правила, па чак и грешке везане за тему логаритама. Успјеси у учењу!