Материјална тачка: дефиниција, вредности, примери и решавање проблема

Шта је материјална тачка? Које су физичке величине повезане с њом, за које се опћенито уводи појам материјалне точке? У овом чланку ћемо дискутовати о овим питањима, дати примјере проблема који су повезани са концептом о којем се расправља, као и говорити о формулама које се користе за њихово рјешавање.

Дефиниција

Дакле, која је материјална тачка? Различити извори дају дефиницију у мало другачијем књижевном стилу. Исто се односи и на наставнике на универзитетима, факултетима и образовним институцијама. Међутим, према стандарду, материјална тачка се назива тело, чије димензије (у поређењу са димензијама референтног оквира) могу бити занемарене.

Веза са стварним објектима

Чини се, како можете узети особу, бициклисте, аутомобил, брод, па чак и авион као материјалну тачку, која се углавном бави физичким проблемима када је ријеч о механици покретног тијела? Погледајмо дубље! Да би се у било ком тренутку одредиле координате покретног тела, потребно је знати неколико параметара. То је почетна координата, брзина кретања и убрзање (ако се, наравно, одвија) ​​и вријеме.

Шта је потребно за решавање проблема са материјалним тачкама?

Координатни односи се могу наћи само прикачивањем на координатни систем. Наша планета постаје таква врста координатног система за ауто и друго тело. У поређењу са његовом величином, величина тела се заиста може занемарити. Сходно томе, ако узмемо тело као материјалну тачку, његова координата у дводимензионалном (тродимензионални) простор може и треба да се нађе као координата геометријске тачке.

Кретање материјалне тачке. Задаци

Зависно од комплексности, задаци могу стећи одређене услове. Према томе, на основу датих услова, можемо користити одређене формуле. Понекад, чак и са читавим арсеналом формула, још увијек није могуће ријешити проблем, како кажу, "на главу". Због тога је изузетно важно не само познавати кинематичке формуле које се односе на материјалну тачку, већ и да их можемо користити. То јест, изразити жељену вриједност и изједначити систем једнаџби. Ево основних формула које ћемо применити током решавања проблема:

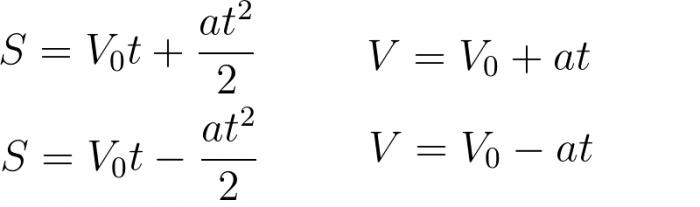
Проблем број 1

Аутомобил, који стоји на стартној линији, нагло почиње да се креће са стационарног положаја. Сазнајте када ће се убрзати до 20 метара у секунди, ако је његово убрзање 2 метра у секунди на квадрат.

Само желим да кажем да је овај задатак практично најједноставнија ствар коју ученик може очекивати. Реч "практично" стоји овде са разлогом. Ствар је у томе да је лакше једноставно заменити директне вредности у формуле. Прво бисмо требали изразити вријеме, а затим направити израчуне. Да бисмо решили проблем, потребна нам је формула за одређивање тренутне брзине (тренутна брзина је брзина тела у одређеном тренутку). Она има следећи облик:

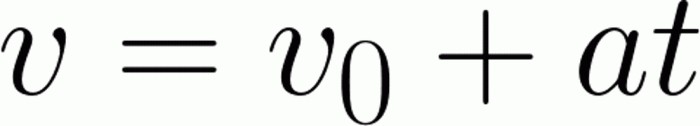
Као што можемо видети, на левој страни једначине имамо тренутну брзину. Тамо апсолутно не требамо. Дакле, радимо једноставне математичке операције: оставимо производ убрзања на неко вријеме на десној страни, и пребацимо почетну брзину улијево. Истовремено треба пажљиво пратити знакове, јер један погрешно остављени знак може радикално промијенити одговор на задатак. Затим помало комплицирамо израз, ослобађајући се убрзања на десној страни: дијелимо га. Као резултат тога, на десној страни, требало би да имамо чисто време, на левој страни, израз на два нивоа. Цела ствар је замењена да изгледа познато. Остаје само да се замене вредности. Дакле, испада да ће аутомобил убрзати за 10 секунди. Важно: ријешили смо проблем, претпостављајући да је у аутомобилу материјална точка.

Проблем број 2

Материјална тачка почиње нагло кочење. Утврдите колика је била почетна брзина у тренутку наглог кочења, ако је 15 секунди прошло пре пуног заустављања тела. Убрзање се узима једнако 2 метра у секунди на квадрат.

Задатак је, у принципу, прилично сличан задатку. Али постоји неколико њихових нијанси. Прво, морамо одредити брзину, коју обично називамо почетном брзином. Односно, у одређеној тачки почиње одбројавање времена и пређеног пута од стране тела. Брзина у овом случају заиста ће пасти под ову дефиницију. Друга нијанса је знак убрзања. Сјетите се да је убрзање векторска величина. Сходно томе, у зависности од правца, он ће променити свој знак. Позитивно убрзање се уочава ако се смјер брзине тијела поклапа са његовим смјером. Једноставно речено, када се тело убрзава. У супротном (то јест, у нашој ситуацији кочења) убрзање ће бити негативно. И ова два фактора треба узети у обзир да би се ријешио овај проблем:

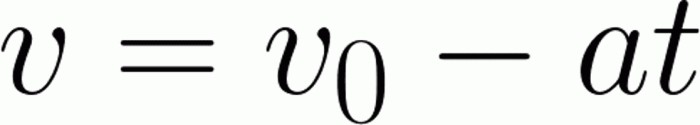
Као и прошли пут, прво изражавамо вриједност која нам је потребна. Да би се избегло збркање са знаковима, остављамо почетну брзину тамо где је. Са супротним знаком, прелазимо на други део једначине, производ убрзања по времену. Пошто је кочење завршено, коначна брзина је 0 метара у секунди. Замјењујући ове и друге вриједности, лако проналазимо почетну брзину. Биће једнако 30 метара у секунди. Лако је приметити да, познавајући формуле, није тако тешко носити се са најједноставнијим задацима.

Проблем број 3

У одређеном тренутку, диспечери почињу да прате кретање ваздушног објекта. Његова брзина у овом тренутку је 180 километара на сат. Након периода од 10 секунди, његова брзина се повећава на 360 километара на сат. Утврдите путању авионом током лета, ако је време лета било 2 сата.

У ствари, у ширем смислу, овај задатак има много нијанси. На пример, убрзање авиона. Јасно је да се наше тело није могло кретати у принципу дуж праволинијске путање. То јест, он треба да узме, да покупи брзину, а онда, на одређеној висини, неки сегмент удаљености треба да се креће у правој линији. Одступања се не узимају у обзир, као и успоравање летења током слијетања. Али то није наш посао у овом случају. Због тога ћемо решити проблем у оквиру школског знања, опште информације о кинематичком кретању. Да бисмо решили проблем, потребна нам је следећа формула:

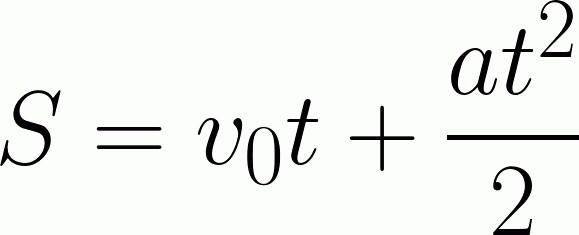
Али овде смо за улов, о чему смо раније разговарали. Познавање формула није довољно - морате их моћи користити. Односно, исписује се једна вредност коришћењем алтернативних формула, проналази је и замењује. Када прегледате почетну информацију која је доступна у задатку, одмах постаје јасно да за њено рјешавање једноставно неће радити. Ништа се не говори о убрзању, али постоје информације о томе како се брзина променила током одређеног временског периода. Тако да можемо сами пронаћи убрзање. Узмите формулу за проналажење тренутне брзине. Она има поглед

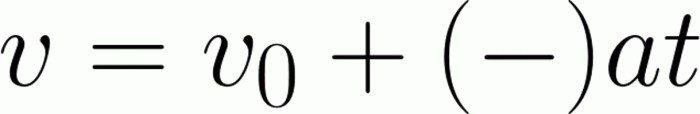
У једном делу остају убрзање и време, а почетна брзина се преноси на другу. Затим раздвајајући оба дела за неко време, пуштамо десну страну. Овде можете одмах израчунати убрзање, замењујући директне податке. Али много је корисније изразити даље. Добијена формула за убрзање се замењује главном. Тамо можете мало смањити варијабле: у нумератору, време је дато у квадрату, ау именитељу у првом степену. Дакле, из овог именитеља можете се отарасити. Па, онда - једноставна замена, пошто нема више шта да се изрази. Одговор би требао бити сљедећи: 440 километара. Одговор ће бити различит ако преведете вредности у другу димензију.

Закључак

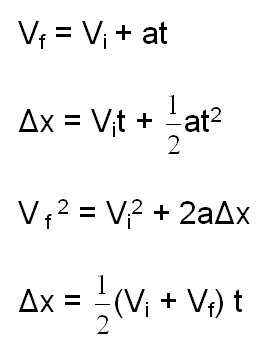
Дакле, шта смо сазнали током овог чланка?

1) Материјална тачка је тело чије димензије се могу занемарити у односу на величину референтног система.

2) Да би се решили проблеми повезани са материјалном тачком, постоји неколико формула (датих у чланку).

3) Знак убрзања у овим формулама зависи од параметра кретања тела (убрзање или успоравање).