Остроградски - Гауссова теорема и формула

Мв Остроградски - руски математичар и физичар од Руског царства, академик. Он је дао огроман допринос развоју математичка анализа теорија вероватноће, механика (одељак физике) теорија бројева. Године 1826. извукао је формулу, сада названу Остроградски-Гаусс формула.

Историја открића

Остроградско-Гауссову формулу први пут помиње Јосепх Лагранге 1762. године.

Даље, главни метод редукције троструког интеграла на површину доказао је Карл Гаусс, који је као основ за доказивање користио решавање проблема у електродинамици. То се десило у првој половини КСИКС века.

Даље, формулу у општој форми представио је Михаил Остроградски. Уз његову помоћ, постало је могуће изразити вриједност диференцијала у параметру из Н-пута интеграла.

Значење формуле Остроградски

Остроградско-Гаусова формула повезује троструки интегрални изнад просторног волумена са интегралом на површини на лицу. То је аналогни Грееновој формули, која повезује двоструки интеграл преко равнине са кривочулним правцем дуж њених граница.

Извођење формуле

Остроградски - Гауссова формула: закључак. Претпоставимо да је у домену В дефинисана интеграндска функција Р (к, и, з), која је дефинитивна и континуирана. Његов дериват је сличан у целом домену В, укључујући и његову границу. У овом облику, сада је позната Остроградски - Гауссова теорема (формула је дата испод).

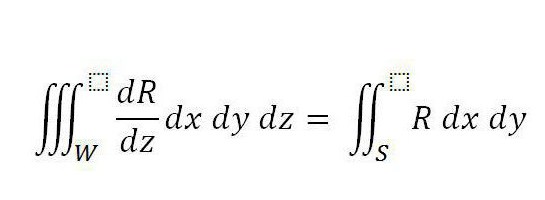
Штавише, С је површина која граничи тело, а интегрални део са десне стране је распоређен на њену спољну страну.

И апсолутно истина

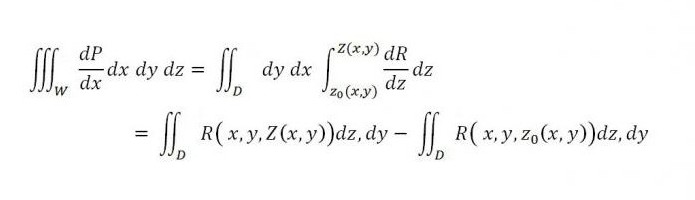
Ако на сличан начин узмемо у обзир интеграле на површини, онда

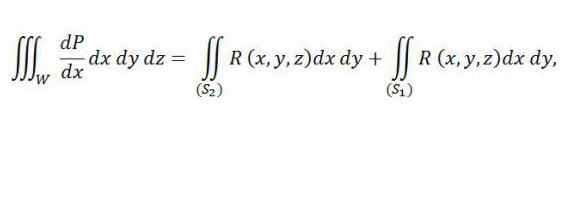
док је са десне стране сума два интеграла - прва се односи на горњи део површине (С ₂ ), а други - на доњи део површине (С ₁ ). Ако овом једнакости на десној страни додамо интегрални ниже, онда његова ваљаност неће бити нарушена:

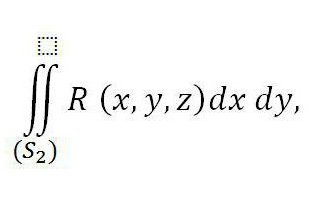
Одговара спољашњем делу површине С3 због једнакости нули.

Ако комбинујемо сва три горенаведена интеграла у један, добићемо посебан случај формуле Остроградски.

Лако је схватити да је ова формула истинита за ширу класу тела и важи и за фигуре ограничене апсолутно свим нелинеарним површинама.

Следеће формуле су сличне:

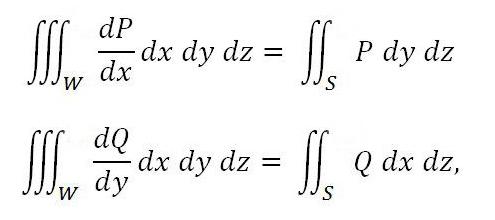
ако су функције К и П континуиране у домени заједно са њиховим дериватима дП / дк и дК / ди.

Ако додамо обе једнакости, добијемо израз за Остроградску формулу. Приказује интеграл преко површине, повезан са спољним делом површине, преко троструког интеграла, који се преузима преко самог тела, а граница је горе поменуте површине.

Треба схватити да формуле Зелена, Стокеса и Остроградског изражавају интеграл који је повезан са одређеним геометријским телом, кроз интеграл који се узима на његовој граници. Греенова формула се користи само у случају дводимензионалности простора, Стокесова формула се примјењује на закривљени дводимензионални простор.

Невтон-Леибнизова формула се такође може сматрати неким аналогом ових формула, али за једно-димензионални простор.

Употреба ове формуле

Нека су континуиране функције А, Б и Ц дате у било којој неотвореној области простора, узимајући у обзир било коју затворену површину која се налази у датом подручју и ограничавајући одређено тело, можемо узети у обзир следећи интегрални део по површини:

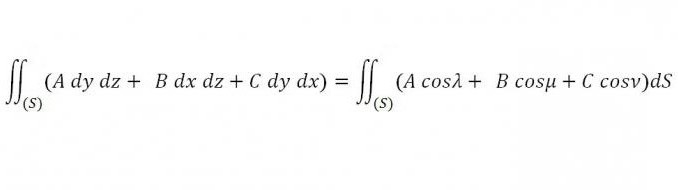
Неопходно је пронаћи такве вредности А, Б и Ц, тако да је за сваки к, и и з овај интеграл једнак нули.

Да бисте то урадили, користите Остроградски-Гаусс формулу. Један од претпостављених услова је извесност и континуитет функција А, Б и Ц и њихових деривата.

Такође је потребно специфично увести најодређеније ограничење за одређени случај: и тело и гранична површина морају се истовремено налазити у одређеној и специфичној области, која се назива једноставно повезана. Његова главна карактеристика је одсуство празног простора (укључујући и простор тачке). Тако ће граница тела бити једна и са тим ће бити једна површина.

Након примене формуле, могуће је добити следећи услов, који је довољан:

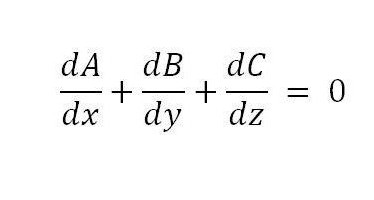
Да би се доказало да је услов такође неопходан, довољно је користити диференцијацију троструког интеграла.

У закључку, потребно је рећи о подручјима употребе.

Како се формула Остроградски-Гаусс користи у пракси? Примјери употребе могу се наћи у различитим пољима: извести неке формуле у физици (на примјер, дифузна једнаџба), трансформирати интеграле, израчунати Гауссове интеграле, доказати неке формуле, и још много тога.