Својства и формуле правокутне призме

Призма је једна од савршених волуметријских фигура, заједно са лоптом, цилиндром и пирамидом, о чијим се особинама расправља у посебном одељку геометрије - стереометрија. У овом чланку разматрамо главне карактеристике правокутне призме.

Присм фигуре

Многи људи знају о троугластим призмама или шестерокутним, али не и свака особа има јасну предоџбу о томе шта је та цифра уопште. У геометрији, под њом се разуме просторни објекат који је ограничен са два идентична полигона и неколико четверокута. Два полигона се називају базе призме. Они леже паралелно. Сви четверокути су паралелограми и формирају бочну површину слике.

Главне формуле и својства призме односе се на питања одређивања запремине, површине њене површине и броја елемената који формирају ту фигуру. Састав потоњих укључује врхове, ивице и лица. Количине ових елемената су међусобно повезане Еулеровим изразом за полиедре. Она има следећи облик:

Број ивица = број лица + број врхова - 2

Пошто је бочна површина призме увек представљена паралелограмима, њене главне карактеристике зависе од типа полигона који лежи у основи ове фигуре. Ако је полигон троугао, онда се призма назива троугластом, ако је четверокут четверокутан, и тако даље.

Правоугаона призма

Ако је угао између сваке стране призме и његове базе 90 ^° , онда се таква фигура назива правокутна. Имајте на уму да говоримо о куту између страна, а не између ребара. Често се таква фигура назива директна призма.

Када је означени угао 90 ^о , сви паралелограми аутоматски постају правоугаоници. Ово је још један разлог зашто се ова призма назива правокутна. Слика испод показује како изгледа правокутна призма.

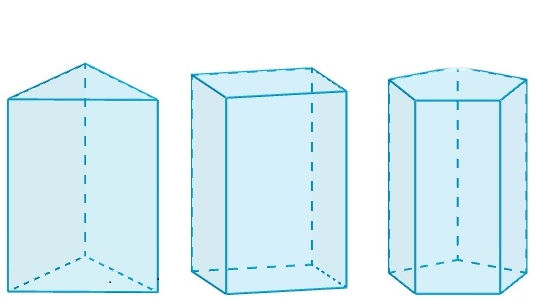
Овде видимо да се свака од три призме разликује од осталих по типу полигона који лежи у основи. На слици су приказане трокутасте, четверокутне и петерокутне призме. Број правоугаоника за сваки од њих је 3, 4 и 5, редом.

Важно својство правокутне призме, која га разликује од косог угла, јесте чињеница да се дужина њене бочне ивице поклапа са висином фигуре. Ово својство је веома погодно за израчунавање његове површине и запремине.

Исправна призма

Свака директна призма на којој лежи правилан полигон назива се регуларна. Наведени полигон мора имати исту дужину свих страна и једнаке углове. Такав правоугаоник је једнакостраничан трокут, квадрат, пентагон и тако даље.

На доњој слици приказана су два призме. Лева је тачна, јер је у њеној основи квадрат и она је равна. Десна, упркос чињеници да је линија равна, није тачна, јер је њена база произвољни четвороугао.

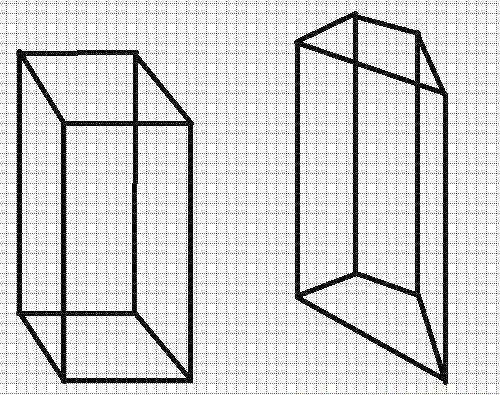
Једина исправна призма која има своје име је коцка. Добија се када се висина фигуре подудара са дужином стране квадрата у бази.

Будући да је подручје за регуларни полигон лако израчунати, тада је за сваку регуларну призму познате формуле за његову површину и волумен.

Подручје правилног полигона

Прије давања формула за површину и волумен правокутне призме, размотрите правилан полигон.

На доњој слици приказан је скуп регуларних полигона, са изузетком круга.

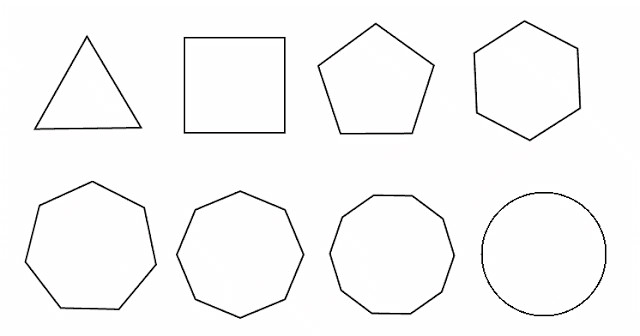
Видљиво је да се за сваку од њих број страна подудара са бројем углова. Штавише, све стране и углови су исти. Ова својства нам омогућавају да дамо формулу која је универзална за све правилне полигоне и омогућава нам да израчунамо њихову површину. Формула има форму:

С _н = н / 4 * а ² * цтг (пи / н)

Где је а дужина стране, н је број страна (врхова) облика. Симбол цтг означава котангентну тригонометријску функцију.

Показујемо како да користимо овај израз. На пример, израчунајмо подручје једнакостраничног троугла. За њега н = 3, онда:

С ₃ = 3/4 * а ² * цтг (пи / 3) = 3/4 * а ² * 1 / =3 = √ 3/4 * а ²

Сада користите ову формулу за квадрат. Имамо:

С ₄ = 4/4 * а ² * цтг (пи / 4) = а ² * 1 = а ²

То јест, добили смо познати израз за квадрат квадрата.

Површина призме

Када је дата геометријска дефиниција дотичне фигуре, показано је да се састоји од две базе и више паралелограма. Овај број је потпуно једнак броју страна полигона у бази. Површина разматране фигуре може се записати следећом формулом:

С = 2 * С _о + С _б

Где је С _о - основна површина, С _б - бочна површина. Пошто се потоњи састоји од н паралелограма, његова вредност је једнака збиру њихових области.

У случају правилне равне призме, бочна површина ће бити формирана правоугаоницима са странама а и х, где је а дужина основне стране, х је висина призме. За случај н правилног квадрата добијамо формулу за подручје С _тот призме:

С _тот = н / 2 * а ² * цтг (пи / н) + н * а * х

На доњој слици приказано је скенирање шестерокутне призме.

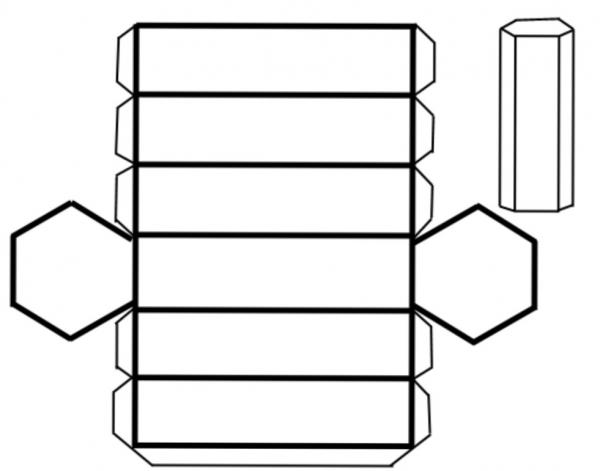
Може се видети да је фигура формирана са два правилна шестерокута и шест идентичних правоугаоника, чија је једна страна једнака страни шестерокута. Примјењујући израз изнад за ову призму, добијамо:

С ⁶ _тот = _6/2 * а ² * цтг (пи / 6) + 6 * а * х = 3 * а * (*3 * а + 2 * х)

Формула за запремину

Обим призме се генерално израчунава користећи следећу једноставну формулу:

В = С _о * х

За правоугаони облик, висина је њена ивица, тако да је овај израз лако применљив. На пример, израчунавамо волумен за троугласту регуларну призму. Површина њене базе је већ израчуната, једнака је:

С ₃ = /3 / 4 * а ²

Онда ће вредност волумена за облик бити следећа:

В = С ₃ * х = /3 / 4 * а ² * х

Формуле за равну призму са регуларним полигоном на дну показују да се сва својства за такве бројке могу добити ако знате само два параметра: дужину стране н-кута и висину призме.