Квадратне једначине. Решавање квадратних једначина
У почетку, ова тема може изгледати компликовано због многих не баш једноставних формула. Не само да квадратне једначине имају дугачке уносе, већ се и корени налазе и преко дискриминанта. Постоји укупно три нове формуле. Није лако запамтити. То је могуће тек након честог решења таквих једначина. Тада ће све формуле бити запамћене саме од себе.

Општи преглед квадратне једначине
Овде им се нуди експлицитан запис, када се прво забележи највећи степен, а затим - у опадајућем редоследу. Често постоје ситуације када су компоненте међусобно супротне. Тада је боље преписати једнаџбу редослиједом опадања степена варијабле.
Представљамо запис. Оне су приказане у табели испод.
| Ознака величине | Њено име |
| а, б, ц | коефицијенти који су произвољни бројеви |
| к | променљива |
| Д | дискриминантни |
| к 1 к 2 | корени једначине |
Ако прихватимо ове ознаке, све квадратне једначине се сведу на следећи унос.
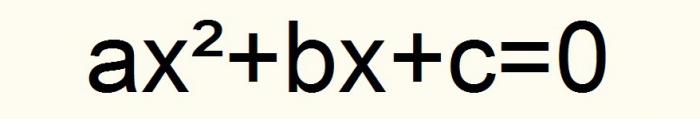
Штавише, коефицијент а = 0. Нека ова формула буде означена бројем један.
Када је дата једначина, нејасно је колико ће коријена бити у одговору. Зато што је једна од три опције увек могућа:
- решење ће имати два корена;
- одговор је један број;
- корени једначине уопште неће бити.
И док одлука није завршена, тешко је схватити која од опција ће пасти у конкретном случају.
Типови записа квадратних једначина
У задацима могу постојати различити уноси. Они неће увек изгледати као општа формула за квадратну једначину. Понекад ће пропустити неке од ставки. Оно што је горе написано је комплетна једначина. Ако уклоните други или трећи појам, добијете нешто друго. Ови записи се зову и квадратне једначине, само непотпуне.
Штавише, само појмови чији су коефицијенти „у“ и „ц“ могу нестати. Број "а" не може бити нула под било којим условима. Зато што се у овом случају формула претвара у линеарну једначину. Формуле за некомплетну форму једначина су следеће:
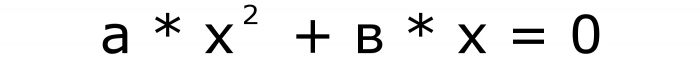
и
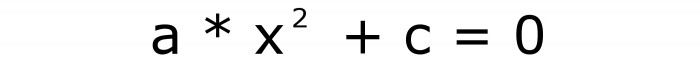
Дакле, постоје само два типа, поред пуних, постоје и непотпуне квадратне једначине. Нека прва формула буде број два, а друга три.
Дискриминантан и зависност броја корена од његове вредности
Морате знати овај број да бисте израчунали корени једначине. Увек се може израчунати, без обзира на формулу квадратне једначине. Да бисте израчунали дискриминантну особу, морате користити доњу једнаџбу која ће имати број четири.

После замене вредности коефицијената у овој формули, можете добити бројеве са различитим знаковима. Ако је одговор да, онда ће одговор на једначину бити два различита корена. Са негативним бројем, корени квадратне једначине ће бити одсутни. У случају једнакости нули, одговор ће бити један.
Како се решава квадратна једначина комплетног облика?
Заправо, разматрање овог питања је већ почело. Зато што прво морате да пронађете дискриминанта. Када је јасно да постоје корени квадратне једначине, а њихов број је познат, потребно је користити формуле за варијабле. Ако постоје два корена, онда морате да примените ову формулу.
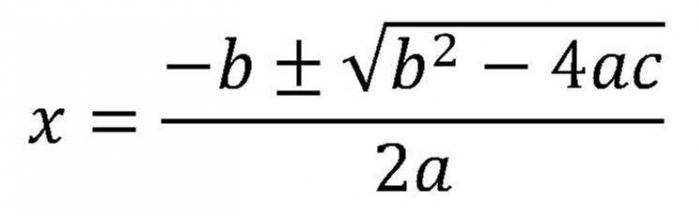
Пошто се у њему налази “±” знак, биће две вредности. Израз квадратног корена је дискриминантан. Стога се формула може другачије написати.
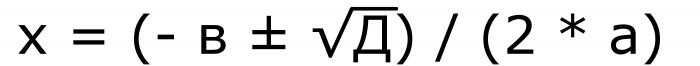
Формула пет. Из истог записа јасно је да ако је дискриминант нула, онда ће оба коријена узети исте вриједности.
Ако решење квадратних једначина још није разрађено, боље је записати вредности свих коефицијената пре примене дискриминантних и променљивих формула. Касније овај тренутак неће изазвати потешкоће. Али на самом почетку постоји конфузија.
Како је решена квадратна некомплетна једначина?
Овде је све много једноставније. Чак и нема потребе за додатним формулама. И не требају они који су већ забележени за дискриминанту и непознато.
Прво ћемо размотрити некомплетну једначину број два. У овој једнакости, претпоставља се да се непозната вриједност стави из заграде и ријеши линеарна једнаџба која ће остати у заградама. Одговор ће бити два корена. Први је нужно једнак нули, јер постоји фактор који се састоји од саме променљиве. Други ће се појавити на одлуци линеар екуатион.
Непотпуна једнаџба број три рјешава се пребацивањем броја с лијеве стране једнакости у десно. Онда морате поделити са коефицијентом према непознатом. Остаје само да се извади скуаре роот и запамтите да је запишете два пута са супротним знаковима.

Корисни савети
Затим, записујемо неке радње које нам помажу да научимо како да решимо све врсте једнакости које се претварају у квадратне једначине. Они ће помоћи ученику да избегне непажње. Ови недостаци су узрок лоших процјена у проучавању опсежне теме "Квадратне једнаџбе (разред 8)". Након тога, ове акције неће морати стално да се изводе. Зато што ће постојати стална вештина.
- Прво морате написати једнаџбу у стандардном облику. То јест, прво израз са највећим степеном варијабле, а затим - без степена и последњег - само број.
- Ако се испред коефицијента “а” појави минус, онда може компликовати рад за почетника да проучи квадратне једнаџбе. Боље је да га се отарасиш. У ту сврху, сва једнакост мора бити помножена са "-1". То значи да ће сви термини промијенити знак у супротно.
- На исти начин се препоручује да се ослободите фракција. Једноставно помножите једнаџбу са одговарајућим множитељем тако да су именитељи смањени.

Примери
Потребне су следеће квадратне једначине:
к 2 - 7к = 0;
5к 2 - 30 = 0;
15 - 2к - к 2 = 0;
к 2 + 8 + 3к = 0;
12к + к 2 + 36 = 0;
(к + 1) 2 + к + 1 = (к + 1) (к + 2).
Прва једначина: к 2 - 7к = 0. Непотпуна је, дакле, ријешена је као што је описано за формулу два.
Након стављања заграда, к (к - 7) = 0.
Први корен узима вредност: к 1 = 0. Други ће се наћи из линеарне једначине: к - 7 = 0. Лако је приметити да је к 2 = 7.
Друга једначина: 5к 2 + 30 = 0. Опет непотпуна. Решава се само као што је описано за трећу формулу.
Након пребацивања 30 на десну страну једначине: 5к 2 = 30. Сада треба да се подели са 5. Испада: к 2 = 6. Одговори ће бити бројеви: к 1 = ,6, к 2 = - .6.
Трећа једначина: 15 - 2к - к 2 = 0. У даљем тексту, решење квадратних једначина ће почети са њиховим поновним уписивањем у стандардни облик: - к 2 - 2к + 15 = 0. Сада је време да користимо други користан савет и помножимо све са минус један . Испоставља се да је к 2 + 2к - 15 = 0. Према четвртој формули, дискриминант се мора израчунати: Д = 2 2 - 4 * (- 15) = 4 + 60 = 64. То је позитиван број. Из горе наведеног, испада да једначина има два корена. Потребно их је израчунати по петој формули. То значи да је к = (-2 ± )64) / 2 = (-2 ± 8) / 2. Онда к 1 = 3, к 2 = - 5.
Четврта једнаџба к 2 + 8 + 3к = 0 претвара се у ово: к 2 + 3к + 8 = 0. Његова дискриминантна је једнака тој вриједности: -23. Пошто је овај број негативан, одговор на овај задатак ће бити сљедећи унос: "Нема коријена".
Пета једначина 12к + к 2 + 36 = 0 треба поново написати на следећи начин: к 2 + 12к + 36 = 0. Након примене формуле за дискриминант, добијамо број нула. То значи да ће имати један корен, наиме: к = -12 / (2 * 1) = -6.
Шеста једнаџба (к + 1) 2 + к + 1 = (к + 1) (к + 2) захтијева трансформације, које се састоје у довођењу тих термина на мјесто прије отварања заграда. На мјесту првог појавит ће се сљедећи израз: к 2 + 2к + 1. Након једнакости, појавит ће се овај запис: к 2 + 3к + 2. Након што се такви појмови броје, једнаџба ће изгледати као: к 2 - к = 0. Претворила се у непотпуна . Сличан њему се већ сматрао мало вишим. Корени овога ће бити бројеви 0 и 1.