Знакови, саставни елементи и својства једнакокрачног троугла

Први историчари наше цивилизације - стари Грци - спомињу Египат као родно место геометрије. Тешко је с њима се не слагати, знајући са каквом је огромном прецизношћу подигнуте дивовске гробнице фараона. Међусобно распоређивање пирамидалних равни, њихових пропорција, оријентације дуж кардиналних тачака - било би незамисливо да се постигне такво савршенство без познавања основа геометрије.

Реч "геометрија" може се превести као "димензија Земље". И реч "земља" се не појављује као планета - део Сунчевог система, већ као авион. Обележавање подручја за пољопривреду је, највјероватније, полазна основа науке о геометријским облицима, њиховим врстама и својствима.

Троугао је најједноставнија просторна фигура планиметрије, која садржи само три тачке - врхове (не може бити мање). Основа темеља може бити зашто се у њему појави нешто тајанствено и древно. Свевидеће око у троуглу је један од најранијих познатих окултних знакова, а географија њене дистрибуције и временског оквира су једноставно невероватни. Од древних, египатских, сумерских, астецких и других цивилизација до модернијих заједница љубитеља окултизма, раштрканих широм свијета.

Шта су трокути

Уобичајени вишеструки троугао је затворена геометријска фигура која се састоји од три сегмента различите дужине и три угла, од којих ниједан није у праву. Поред тога, постоји неколико посебних типова.

Акутни троугао има све углове мање од 90 степени. Другим речима - сви углови таквог троугла су оштри.

Прави троугао преко којих су ученици стално плакали због обиља теорема, има један угао са магнитудом од 90 степени или, како се још назива, равном линијом.

Тупи троугао се разликује по чињеници да је један од његових углова туп, то јест, његова магнитуда је већа од 90 степени.

Еквивалентни троугао има три стране исте дужине. Таква фигура такође има све углове.

Коначно, у једнакокрачном троуглу са три стране, два су једнака.

Дистинцтиве феатурес

Својства једнакокрачног трокута такођер одређују његову главну, главну, разлику - једнакост двије стране. Ове стране које су једнаке једна другој називају се бедрима (или, чешће, бочним странама), али се трећа страна назива "темељ".

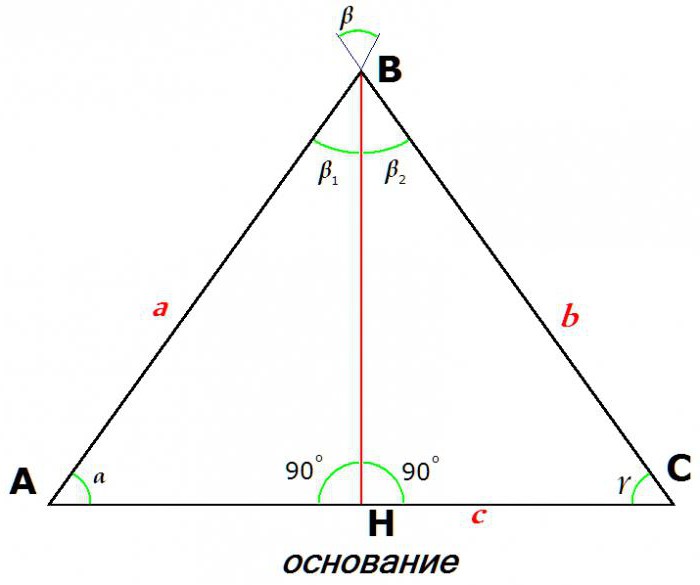
На овој слици, а = б.

Други знак једнакокрачног троугла произилази из сине теореме. Пошто су стране а и б једнаке, синуси њихових супротних углова су једнаки:

а / син γ = б / син α, одакле имамо: син γ = син α.

Једнакост синуса подразумијева једнакост углова: γ = α.

Дакле, други знак једнакокрачног троугла је једнакост два угла сусједна бази.

Трећи знак. Троугао разликује елементе као што су висина, симетрала и медијана.

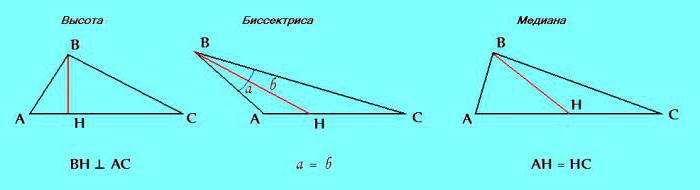
Ако се у процесу решавања проблема испостави да су у посматраном троуглу два од ових елемената исти: висина са бисецтор; бисецтор са медиан; медиан са висином - дефинитивно је могуће закључити да је троугао једнакокрачан.

Геометријска својства слике

1. Својства једнакокрачног троугла. Једно од разликовних својстава фигуре је једнакост углова сусједних база:

α = γ;

<ИОУ = <БЦА.

2. Друга особина о којој смо већ говорили: медијан, симетрала и висина у једнакокрачном троуглу се поклапају ако су грађени од њеног врха до базе.

3. Једнакост симетрала извучених из врхова у бази:

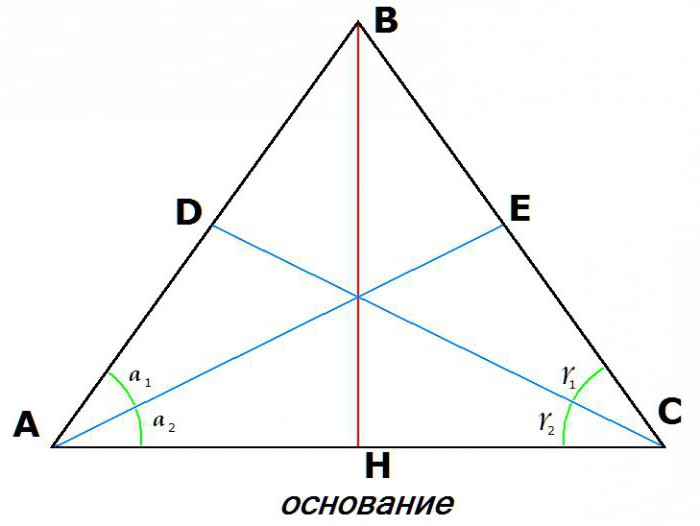
Ако је АЕ симетрала угла ИОУ, а ЦД је симетрала угла БЦА, онда: АЕ = ДЦ.

4. Својства једнакокрачног трокута такођер осигуравају једнакост висина, које се извлаче из врхова у бази.

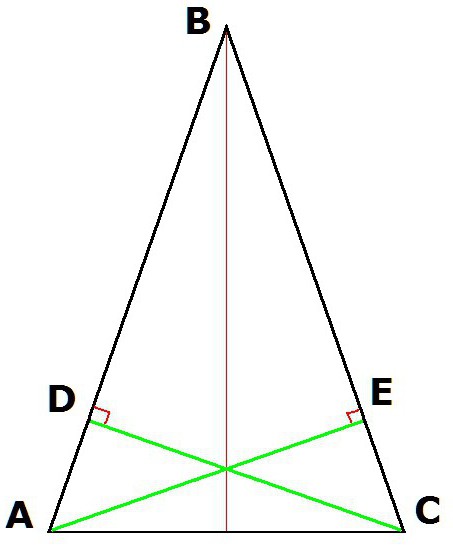
Ако конструишемо висине троугла АБЦ (где је АБ = БЦ) из врхова А и Ц, онда ће настали сегменти ЦД и АЕ бити једнаки.

5. Медијане извучене из углова у бази такође ће бити једнаке.

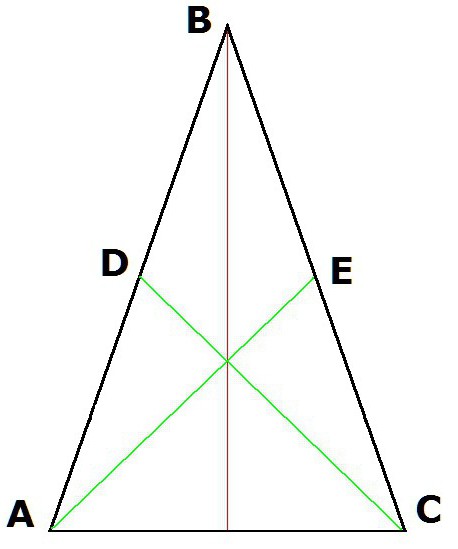
Дакле, ако су АЕ и ДЦ медијан, то јест, АД = ДБ, и БЕ = ЕЦ, онда АЕ = ДЦ.

Висина троугла троугла

Једнакост страна и углова на њима додаје неке посебности израчунавању дужина елемената разматране фигуре.

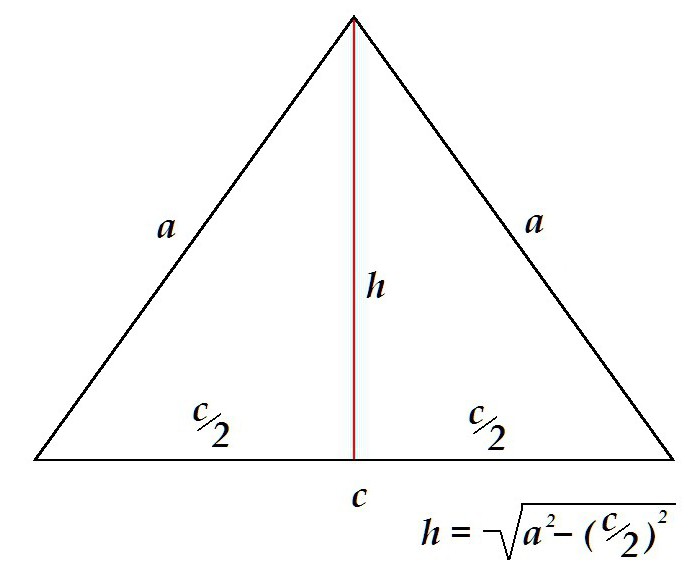
Висина у једнакокрачном троуглу дели фигуру на 2 симетрична правоугаона троугла са хипотенусима у којима стране пројектују. Висина у овом случају одређена је Питагореровом теоремом као нога.

Троугао може имати све три стране једнаке, онда ће се звати једнакостран. Висина у једнакостраничном троуглу одређена је на исти начин, само за израчуне довољно је знати само једну вриједност - дужину стране овог трокута.

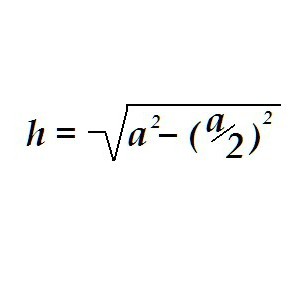
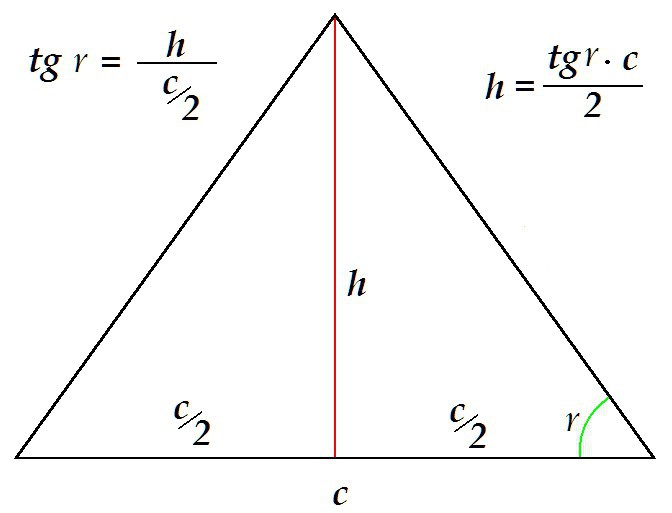
Могуће је одредити висину на други начин, на пример, познавање базе и угла поред њега.

Медијан једнакокрачног троугла

Разматрани тип троугла, због својих геометријских карактеристика, решава се једноставно једноставним минималним скупом изворних података. Пошто је медијан у једнакокрачном троуглу једнак и његовој висини и бисектрикси, алгоритам за одређивање не разликује се од реда у којем су ти елементи израчунати.

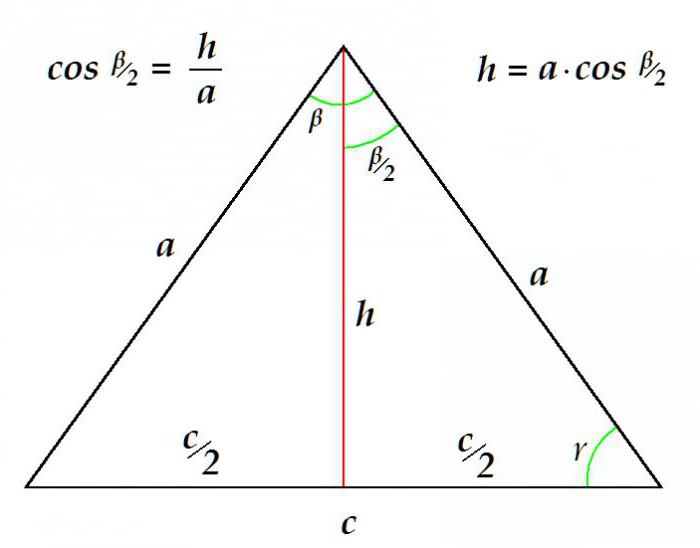
На пример, можете одредити дужину медијана према познатој страни и угао на врху.

Како одредити периметар

Пошто се у разматраној планиметричној фигури две стране увек изједначавају, онда је за одређивање обима довољно знати дужина базе и дужина једне од страна.

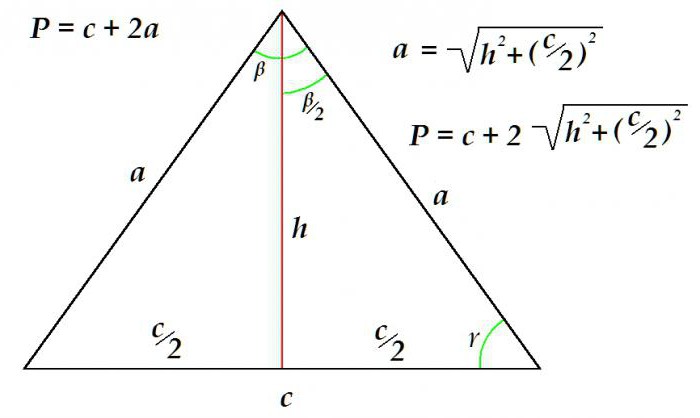
Размотрите пример када дефинисати обод троугла по познатој бази и висини.

Периметар је једнак збиру базе и двострукој дужини стране. Са друге стране, страна се одређује коришћењем Питагорине теореме као хипотенузе правог троугла. Његова дужина је једнака скуаре роот од сума квадрата висине и квадрата половине базе.

Површина једнакокрачног троугла

Постоје, по правилу, потешкоће и израчунавање површине једнакокрачног троугла. Универзално правило за одређивање површине троугла као половине продукта базе до његове висине, наравно, важи иу нашем случају. Међутим, својства једнакокрачног троугла чине задатак лакшим.

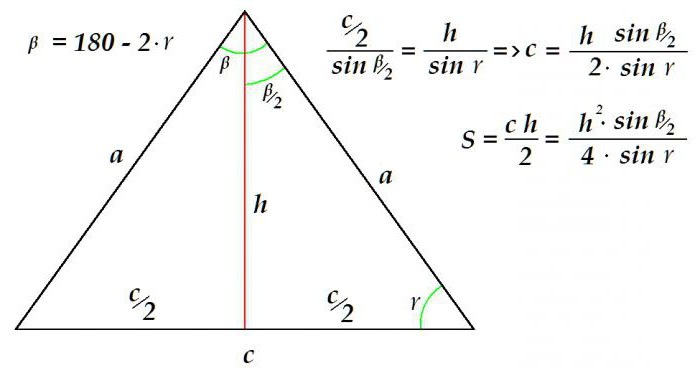
Претпоставимо да су висина и угао уз базу познати. Потребно је одредити подручје слике. То се може урадити на овај начин.

Пошто је збир углова било ког троугла 180 °, онда је лако одредити угао. Даље, употребом пропорције састављене према синусној теореми, одређује се дужина базе троугла. Све, основа и висина - довољно података за одређивање подручја - су доступни.

Остала својства једнакокрачног троугла

Положај центра кружнице описан око једнакокрачног трокута зависи од угла врха. Дакле, ако је једнакокраки троугао акутан, центар круга се налази унутар фигуре.

Центар круга, који је описан око једнакокраког троугла с тупим странама, лежи изван њега. И на крају, ако је угао на врху 90 °, центар лежи тачно на средини базе, а пречник круга пролази кроз базу.

Да би се одредио радијус кружнице описан око једнакокрачног троугла, довољно је поделити дужину стране двоструким косинусом од пола угла на врху.