Знаци сличности троуглова и њихова практична примена за решавање проблема

Појам сличности произвољан геометријски облици у суштини, веома је лако објаснити, а још мање доказати. Тако, на пример, гледајући предмет кроз лупу, видимо слику овог објекта неколико пута увећану са пропорцијама свих њених димензија. Другим речима, слика објекта је слична оригиналном објекту пре увећања. У већини проблема геометрије, доказати пропорционалност страна и троугла примените 3 главна знака. Да би се узели у обзир постојећи знаци сличности троуглова, неопходно је у почетку дефинисати кључни концепт који ће се користити у тексту у будућности.

Дакле, троуглови су слични, ако су њихове слично смјештене стране пропорционалне, а одговарајуће распоређени кутови су једнаки (ваља имати на уму да се стране називају сличним, или одговарајућим, ако се налазе наспрам истих углова). Размотримо сличне троуглове ЦАБЦ и 1А ₁ Б ₁ Ц ₁ . Према наведеном концепту, релевантне стране су: АБ и А ₁ Б ₁ , као и парови страна БЦ и Б ₁ Ц ₁ , АЦ и А ₁ Ц ₁ . Имајте на уму да стране сваког од ова три пара леже насупротни углови исте величине.

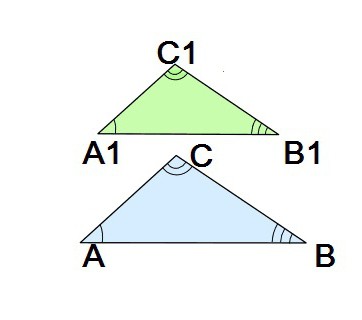Сличност је означена посебан карактер који се налази између ознака у питању: ЦАБЦ ₁ Б А ₁ Б ₁ Ц ₁ .

Однос релевантних страна са присуством ове особине је параметар који се назива коефицијент сличности к. Ако је к = 2, онда можемо рећи да је једна од две разматране геометријске фигуре увећана дупла копија друге. Јасно је да ако је к = 1, онда су троуглови једнаки. Дакле, ова једнакост се може сматрати посебним случајем њихове сличности.

Знаци сличности троуглова

Испоставља се да, да би се утврдило присуство разматраног обиљежја, нема потребе провјеравати све захтјеве наведене у тексту горе наведене дефиниције сличности. Довољно је испунити минималне услове, а сада ћемо то потврдити у пракси.

Први знак

Приликом решавања проблема први знак сличности троуглова појављује се у доказима много чешће него други. Имајте на уму да ради само са два елемента геометријске фигуре: два угла. Преостали знаци сличности троуглова захтевају учешће три елемента. Дакле, за два произвољна слична трокута, два угла једног од њих једнака су истим 2 угла другог.

Прооф оф

Према основним својствима која важе за било који произвољни троугао, можемо написати следећи израз за .Ц. Његова вредност ће бити једнака (180 ° - (+А + )В)), за другу ∠С ₁ вредност ће се израчунати по истом принципу. Елементарним трансформацијама израза добијамо да је =Ц = Ц ₁ . Дакле, сви углови присутни у ∆АВС једнаки су свим аналогним угловима који се налазе у ∆А ₁ В ₁ С ₁ . Сличним алгоритмом доказани су и преостали знаци сличности троуглова.

Други знак

Овај приступ доказу се често користи ако су познати углови разматраних геометријских фигура.

За два слична троугла, тачно је да су две стране сваке од њих пропорционалне другој сличној страни друге, а углови између ових парова страна су једнаки.

Прооф оф

Да бисте доказали ову функцију, морате се позвати на претходне израчуне. На основу горе наведених резултата, довољно је доказати да је =В = В ₁ . Размотримо ЦАБЦ ₂ , за које су, према првом знаку, тачне следеће тврдње: = ₁ = 1А ₁ , =2 = В ₁ . ЦАБЦ ₂ ~ 1А ₁ В ₁ С ₁ . То значи АБ / А ₁ Б ₁ = АЦ ₂ / А ₁ Ц. С друге стране, познато је из услова да следећа релација важи: АЦ / А ₁ Ц _{1 =} АБ / А ₁ Б ₁ . Као резултат добијамо једнакост страна АЦ = АЦ ₂ , као и тврдњу да је ЦАБЦ ~ ∆АБЦ ₂ према другом знаку (АЦ = АЦ ₂ и =А = ∠1, будући да је, као резултат разматрања почетних података, утврђено да је А = 1А ₁ и = ₁ = 1А1, АБ- је заједничка страна за ова два троугла). Из доказа следи да ∠Б = ,2, а пошто је =2 = 1В ₁ , добијамо да је =В = В ₁ . Из тога следи да је доказан још један знак.

Трећи знак

Ова особина се сматра најочигледнијом када се доказује сличност, јер се разматрају све стране ових троуглова са познатим параметрима.

Дакле, за два троугла која су слична један другом, постоји тврдња да су 3 стране једне од њих пропорционалне 3 одговарајуће стране друге.

Прооф оф

С обзиром на претходну карактеристику сличности, сада је за конструкцију доказа довољно само утврдити да постоји једнакост облика: =А = 1А ₁ . Да бисте то урадили, узмите у обзир било које произвољно ЦАБЦ ₂ , за које је ∠1 = 2А ₁ , 2 = В ₁ . Према првом атрибуту ЦАБЦ ₂ ∆ ∆А ₁ Б ₁ Ц ₁ , за ова два троугла можемо написати однос типа АБ / А ₁ Б ₁ = БЦ ₂ / Б ₁ Ц ₁ = Ц ₂ А / Ц ₁ А _1, из које можемо написати једнакост облика: Б ₁ Ц ₁ = БЦ ₂ , А ₁ Ц ₁ = АЦ ₂ . Из овога је логично закључити да ∆АБЦ ∆ ∆АБЦ _2, и, као закључак, АндА и 1А1 су једнаки. Из тога следи да је и разматрана особина доказана.

Пропертиес

1. За два троугла, слична један другом, однос вредности њихових области је директно пропорционалан квадрату коефицијента. Прооф. Размотримо две произвољне фигуре које имају три стране и три угла који су слични један другом. Нека су А и А ₁ одговарајуће стране ових фигура, а х и х ₁ су одговарајуће висине. Нека је к коефицијент сличности за разматране троуглове, тако да из аспекта односа можемо написати једначину форме: А ₁ = к * А. Лако је видети да за однос висине можемо написати једначину форме: х ₁ = к * х. За однос површина разматраних геометријских фигура добијамо: С ₁ / С = (1 / 2а ₁ х ₁ ) / (1 / 2ах) = (а ₁ / а) * (х ₁ / х) = к * к = к ² . Дакле, када се троугао „растегне“ 2 пута, његова површина се повећава за 2 ² = 4 пута. Друго својство слиједи из претходног доказа и директно је повезано с њим.
2. Све одговарајуће линије нацртане у таквим троугловима су такође пропорционалне једна другој и једнаке вредности горе наведеног коефицијента. Дакле, према горе наведеној имовини, може се тврдити да ће све интерне додатне конструкције бити пропорционалне.

Додавање главне листе знакова

Вреди размотрити неколико појединачних карактеристика које су примјењиве на геометријске облике одређеног типа. Тако да су десни троуглови слични ако:

• њихова хипотенуза и било која од две ноге су пропорционалне;
• ако су њихови одговарајући оштри углови једнаки;
• ако су све ноге разматраних троуглова парно пропорционалне.

Закључак

Тако смо комбиновали све могуће знакове, помоћу којих се некако може доказати сличност две или више фигура са три угла и стране, без обзира на њихов тип и својства. У већини проблема у геометрији, главна три знака се користе за доказивање пропорционалности страна и подручја, али нисмо занемарили низ знакова сличности који су примјењиви само ако је потребно извести доказ за дотичне геометријске фигуре под правим углом. Ови знаци сличности ригхт трианглес увелико поједностављују процес рјешавања разних врста задатака и захтијевају минимум података за њих.