Једноставан задатак: како пронаћи периметар?

Знање како пронаћи периметар, ученици добијају више у основној школи. Тада се ова информација стално користи током курса математике и геометрије.

Општа теорија за све бројке

Странке се обично означавају латиничним словима. Штавише, могу се означити као сегменти. Затим су потребна два слова за сваку страну и написана великим. Или унесите ознаку једног слова, које ће сигурно бити мало.
Слова се увек бирају по абецеди. За троугао ће бити прва три. Шестоугаоник ће имати 6 - од а до ф. Ово је погодно за увођење формула.

Сада како пронаћи периметар. То је збир дужина свих страна слике. Број ставки зависи од његовог типа. Периметар је означен латиничним словом Р. Мјерне јединице се подударају с онима датим за странке.

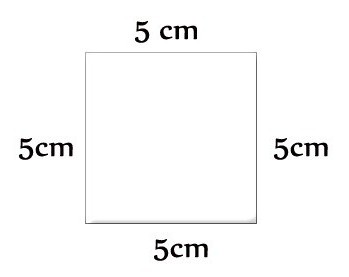
Формуле периметара различитих облика

За троугао: П = а + б + ц. Ако је једнакокрачан, онда се формула претвара: П = 2а + ц. Како пронаћи периметар трокута, ако је једнакостран? То ће помоћи: П = 3а.

За произвољни четверокут: П = а + б + ц + д. Његов посебан случај је квадрат, периметарска формула: П = 4а. Постоји правоугаоник, онда је потребна следећа једнакост: П = 2 (а + б).

Шта ако је непозната дужина једне или више страна троугла?

Искористи предност цосине тхеорем ако постоје две стране података и угао између њих, који је означен словом А. Онда, пре него што нађете периметар, мораћете да израчунате трећу страну. За ово је корисна следећа формула: с² = а² + в² - 2 ав цос (А).

Посебан случај ове теореме формулише Питагора за правоугаони троугао. У њој, косинусна вредност правог угла постаје нула, што значи да последњи термин једноставно нестаје.

Постоје ситуације када треба научити како пронаћи обод троугла може бити на једној страни. Али у исто време, познати су и углови слике. Овде се сине теорема спашава када је однос дужина страна према синусима одговарајућих супротних углова једнак.

У ситуацији када подручје треба да буде препознато од стране подручја, друге формуле ће бити корисне. На пример, ако је познат полупречник уписане кружнице, онда је питање како пронаћи периметар троугла, следећа формула је корисна: С = п * р, овде п је полу-периметар. Она мора бити изведена из ове формуле и помножена са два.

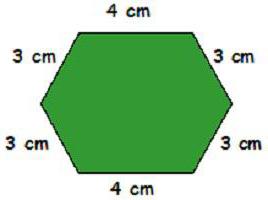
Примери задатака

Стање првог. Научите обод троугла, чије су стране 3, 4 и 5 цм.
Одлука. Потребно је користити једнаџбу, која је горе наведена, и само замијенити податке у проблему вриједности у њу. Прорачуни су једноставни, доводе до броја од 12 цм.
Одговор је. Обим троугла је 12 цм.

Други услов. Једна страна троугла је 10 цм, а познато је да је друга 2 цм већа од прве, а трећа је 1,5 пута већа од прве. Потребно је израчунати његов периметар.
Одлука . Да бисте то сазнали, морате да избројите две стране. Други се одређује као збир 10 и 2, трећи је производ 10 и 1.5. Онда остаје само да се броји сума три вредности: 10, 12 и 15. Резултат ће бити 37 цм.
Одговор је. Обим је 37 цм.

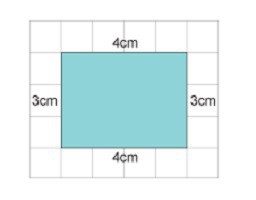
Стање трећег. Има правоугаоник и квадрат. Једна страна правоугаоника је 4 цм, а друга је 3 цм дужа. Потребно је израчунати вриједност стране квадрата, ако је њен обод 6 цм мањи од правокутника.
Одлука. Друга страна правокутника је 7. Знајући то, лако је израчунати његов обим. Израчун даје 22 цм.
Да бисте пронашли страну квадрата, прво морате одузети 6 са периметра правоугаоника, а затим поделити добијени број на 4. Као резултат тога, имамо број 4.
Одговор је. Бочни трг 4 цм.