Симетрала троугла - шта је то?

Геометрија је једна од најсложенијих и најсложенијих наука. Оно што се на први поглед чини очигледним врло ретко се испоставља као тачно. Симптоми, висине, медијани, пројекције, тангенте су огроман број заиста тешких термина са којима се лако може збунити.

У ствари, уз одговарајућу жељу, можете разумети теорију било које сложености. Када је у питању симетрала, медијан и висина, морате разумети да они нису својствени троугловима. На први поглед, ово су једноставне линије, али свака од њих има своја својства и функције, чије познавање знатно поједностављује решавање геометријских проблема. Дакле, која је симетрала троугла?

Дефиниција

Термин "симетрала" потиче од комбинације латинских речи "два" и "рез", "рез", што индиректно указује на његова својства. Обично, када се деца упознају са овим снопом, од њих се тражи да запамте кратку фразу: "Симетрала је штакор који трчи у угловима и преполови угао". Наравно, такво објашњење није погодно за старије студенте, осим што се обично не питају о угљу, већ о геометријски облик. Тако симетрала троугла је зрак који повезује врх троугла са супротном страном, при чему се угао дели на два једнака дела. Точка супротне стране, на коју долази симетрала, за произвољни троугао се бира насумично.

Основне функције и својства

Главна својства овог снопа су мало. Прво, зато што симетрала троугла дели угао на пола, свака тачка која лежи на њој биће на једнакој удаљености од страна које формирају врх. Друго, у сваком троуглу се могу нацртати три бисектрике, према броју доступних углова (због тога ће их већ бити четири у истом четвороуглу и тако даље). Тачка у којој се сва три зрна сијеку је центар круга уписаног у трокут.

Својства су компликована

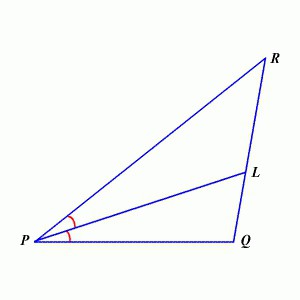
Хајде да мало компликујемо теорију. Још једна интересантна особина: симетрала кута троугла дели супротну страну на сегменте чији је однос једнак односу страна које формирају врх. На први поглед, ово је тешко, али у ствари све је једноставно: у предложеној цифри, РЛ: ЛК = ПР: ПК. Успут речено, ово својство је названо Теорем о Бисектрикси и први пут се појавило у делима старог грчког математичара Еуклида. Запамтили су га у једном од руских уџбеника тек у првој четвртини седамнаестог века.

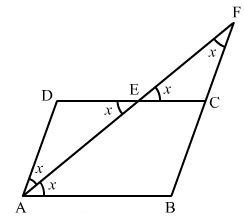
Мало теже. У четверокутници симетрала пресијеца једнакокрачан трокут. Ова слика приказује све једнаке углове за средњи АФ.

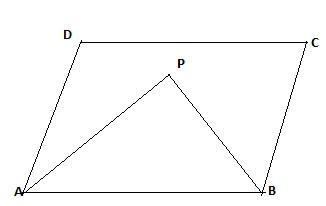
Штавише, у четверокутима и трапезима, симетрале једносмерних углова су окомите једна на другу. На цртежу, угао АПБ-а је 90 степени.

У једнакокрачном троуглу

Једнакокраки једнакокрачан троугао је много кориснији зрак. То је уједно и не само дјелић угла на пола, већ и медијан и висина.

Медијан је сегмент који излази из одређеног угла и пада на средину супротне стране и дели га на једнаке делове. Висина је окомита пала са врха на супротну страну, са њеном помоћи сваки задатак може бити сведен на једноставан и примитиван Питагорин теорем. У овој ситуацији, симетрала троугла је једнака корену разлике између квадрата хипотенузе и друге ноге. Иначе, управо та својства се најчешће налазе у геометријским проблемима.

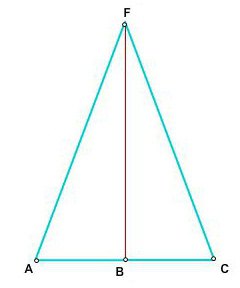
За фиксирање: у овом троуглу, симетрала ФБ је медијан (АБ = БЦ) и висина (углови ФБЦ и ФБА су 90 степени).

Уопштено говорећи

Па, шта треба да запамтиш? Симбол троугла је зрак који дијели свој врх на пола. На сјецишту три зрака је средиште кружнице уписано у овај трокут (једини недостатак ове особине је да нема практичну вриједност и служи само за исправно извођење цртежа). Она такође дели супротну страну на сегменте, чији је однос једнак односу страна између којих је овај зрак прошао. У четверокуту, својства су нешто компликованија, али, да признамо, они се практично не појављују у задацима на нивоу школе, па стога програм обично не утиче на њих.

Симетрала једнакокрачног троугла је крајњи сан сваког ученика. То је у исто време медијан (то јест, дели половину супротне стране) и висину (окомито на ову страну). Решавање проблема са таквом симетралом је сведено на Питагорину теорему.

Познавање основних функција симетрала, као и њених основних својстава, неопходно је за решавање геометријских проблема средњег и високог нивоа сложености. Заправо, овај зрак се налази само у планиметрији, тако да је немогуће рећи да ће памћење информација о њему омогућити да се носи са свим врстама задатака.