Појам кутног момента, његов закон очувања и пример решавања проблема

Ротациони покрет није ништа мање чест у природи од линеарног кретања објеката. Да би се ово потврдило, довољно је подсетити се ротације точкова аутомобила и бицикала, лопатица хеликоптера и навијача, планета око његове осе и око његових звезда. Да би се описао процес кружног кретања објеката, користи се физичка величина, која се назива "кутни момент". Размотрите у чланку шта је то.

Моментум момента честице и оси ротације

У наставку је цртеж који схематски показује да се честица или материјална тачка масе м креће дуж кружне путање радијуса ¯ с брзином ν усмјереном тангенцијално. Оса ротације је окомита на раван слике у тачки О.

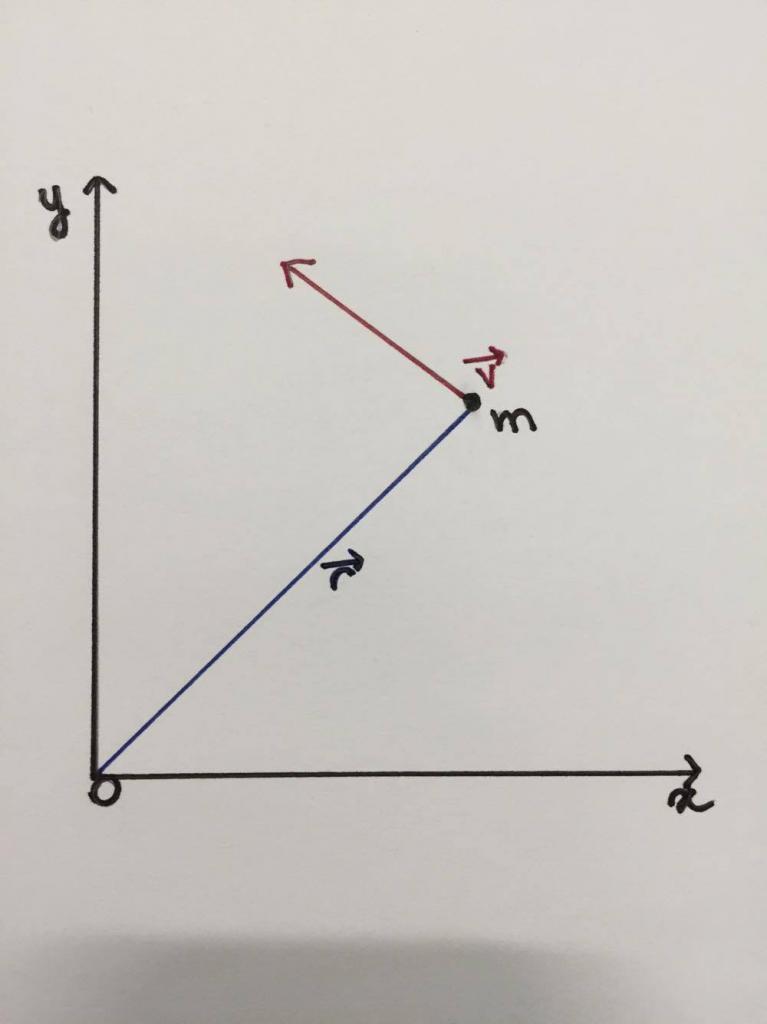
Уведемо следећу физичку величину:

Л¯ = р¯ * м * в¯ = р¯ * п¯.

То се назива кутни момент, или угаони момент. Као што видите, ово је векторска количина. Њен смјер се може одредити правилом десне руке: морате усмјерити 4 прста тако да они, крећући се дуж вектора р¯, дођу до краја вектора п ¯ (или в¯), затим палац показује правац Л¯. У овом случају, Л¯ је усмерен на читач окомит на раван цртања.

Пошто је брзина честице (импулса) на слици усмерена под правим углом према вектору ¯, редукована једначина се може преписати у скаларном облику:

Л = р * м * в = р * п.

Угаона брзина и момент инерције

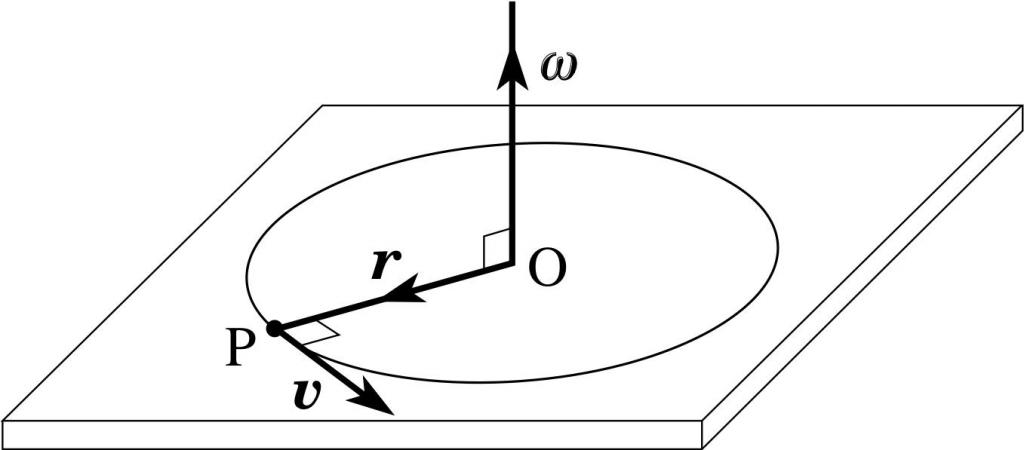
Момент честице из претходног примјера може се записати кроз кутну брзину ω. Да бисмо то урадили, користимо његову везу са линеарном брзином:

ω = в / р => в = ω * р.

Замењујући последњу једначину у скаларну једначину за Л, добијамо:

Л = р ² * м * ω = И * ω, где И = р ² * м.

Овде је И тренутак инерције честице. Резултирајући израз се често користи за рјешавање практичних проблема, од којих ће један бити објашњен у наставку.

Закон очувања ротационог кретања

Кретање у кругу, као и линеарно кретање објеката у простору, карактеришу закони очувања. Једна од њих је очување угаоног момента. Добили смо овај закон.

Једначина разматраног типа кретања има следећи облик:

дЛ / дт = М.

Тамо где дЛ / дт карактерише промену угаоног момента тела током времена, када је под утицајем одређеног тренутка М које стварају спољашње (не унутрашње) силе. Ако је овај момент силе нула, онда лева страна израза нестаје, што значи Л = цонст. За овај случај можемо да напишемо следећу једнакост:

Л = конст = И ₁ * ω ₁ = И ₂ * ω ₂ .

Шта овај запис значи? Каже се да ако се неко тело ротира са брзином ω ₁ и има момент инерције И ₁ , онда се због неких унутрашњих (не спољашњих) сила моменат инерције мења и постаје једнак И ₂ , тада ће нова брзина ротације ω ₂ бити пропорционална повезане са овом променом.

Забиљежени однос се назива закон очувања момента момента точке (тијела) по аналогији с одговарајућим законом за линеарне величине (очување момента), будући да момент инерције И игра улогу масе, а кутна вриједност ω игра улогу масе.

Користећи закон Л = цонст

Однос који се разматра у претходном параграфу може се видети у акцији када наступају клизачи или балерине. Извођењем сложених акробатика, они окрећу своја тела, раштркујући руке и ноге, а затим притисну своје удове уз тело. Посљедње дјеловање доводи до смањења вриједности И и, сходно томе, до повећања брзине ротације, што ствара прилично спектакуларан ефекат.

Још један примјер употребе непромјенљивости момента кретања система је проведба ротације умјетног сателита у свемиру. Да бисте то урадили, покрените посебан замашњак који је причвршћен на њега. Пошто се укупни угаони момент не мења због дејства унутрашњих сила, сам сателит почиње да се ротира у супротном смеру. Чим се окрене на жељени угао око своје осе, замајац се зауставља уз помоћ електричног мотора, а тело сателита такође зауставља своју ротацију.

Израчунајте момент инерције

Пошто је вредност И присутна у закону очувања кружног кретања, треба рећи неколико речи о томе. Она карактерише инерцију система, то јест, како га је "тешко" или "лако" ослободити. На пример, замајац аутомобила има велику масу и релативно велики радијус, тако да је његов момент инерције значајан. Напротив, котач за бицикле је израђен од алуминијумског обода, тако да ћу за то бити релативно мали.

Да бисте израчунали ову физичку карактеристику, користите формулу:

И = ( _м (р ² * дм).

Одатле се види да је момент инерције карактеристика система у који улази тело револуције, а не само тело. Ова чињеница ме разликује од линеарне инерције, која зависи искључиво од својстава тела (његове масе).

Задатак са ротирајућим штапом

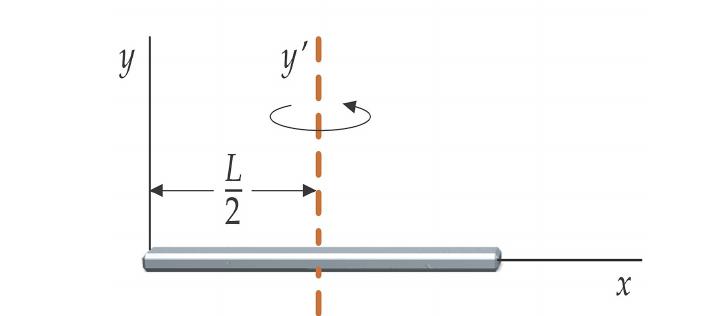
Решићемо занимљив проблем: постоји чврста шипка која се ротира око осе која се налази на њеном крају. Ако се ова оса глатко помери у центар масе шипке, како ће се променити њена брзина ротације?

Ово је класичан задатак примене закона очувања угаоног момента. Тешкоћа је у израчунавању промене момента инерције. Да бисте то урадили, можете користити горњу формулу са интегралом, али ће бити лакше погледати потребне вредности И у референтној литератури.

На почетку, ос ротације је прошла кроз крај штапа. За овај систем, момент инерције је једнак:

И ₁ = м * Л 2/3, где је Л дужина штапа, м је њена маса.

Када је оса помакнута у центар масе објекта, његов момент инерције је промијењен, постао је једнак:

И ₂ = м * Л 2/12.

Применити закон очувања за Л, добијамо:

м * Л 2/3 * ω ₁ = м * Л 2/12 * ω ₂ => ω ₂ / ω ₁ = м * Л 2/3 / (м * Л 2/12) = 4.

Добили смо одговор на проблем: штап ће се ротирати 4 пута брже него на почетку.