Појам матрице и основне дефиниције

Такав концепт као матрица се користи и појављује у секцијама више математике. Најчешће се налази у систему линеарних једначина. Дакле, који је основни концепт матрице? Да би то разумели, није неопходно бити математички геније.

Матрица је нешто што је систем бројева мн, који се у математици пишу у облику табела у којима су м редови, а н су колоне. На његовом пресеку су елементи. Величина матрице зависи од броја редова и колона.

У почетку је разматрана троугласта матрица, али није погодна за решавање сложених једначина, па се у математици користи правоугаони аналог. Такав систем се сматра погодним за рјешавање проблема.

Одакле је дошла матрица

Ако говоримо о првом спомену, концепт матрице је дошао из Кине, или боље речено, био је повезан са "магичним квадратима". Ове табеле сматране су амајлијама због бројева уписаних на њима. У то време није било ни самог концепта матрице, ни начина да се то реши. У неким племенима је одређивала степен сродства, тако да су људи сазнали да ли се могу оженити или не.

Али сам концепт је почетком 19. века увео Јамес Силвестер, који је био енглески математичар. Различити научници радили су на теорији матрица, стварајући комплекс решења за тешке алгебарске проблеме.

Матрица и њени главни типови

Дакле, раније је разматран концепт матрице. Типови матрица су приказани у наставку:

• Мала слова Састоји се од једног реда, тј. Овај тип матрице има број редова тачно м = 1, али је број његових колона произвољан.
• Цолумнар. Ова сорта се састоји само од једне колоне, али може садржати и неколико редова. За ову врсту матрице има свој универзални унос. Означава да се ставке у заградама пишу као колона. Поврх тога, штеди не само простор, већ и вријеме.
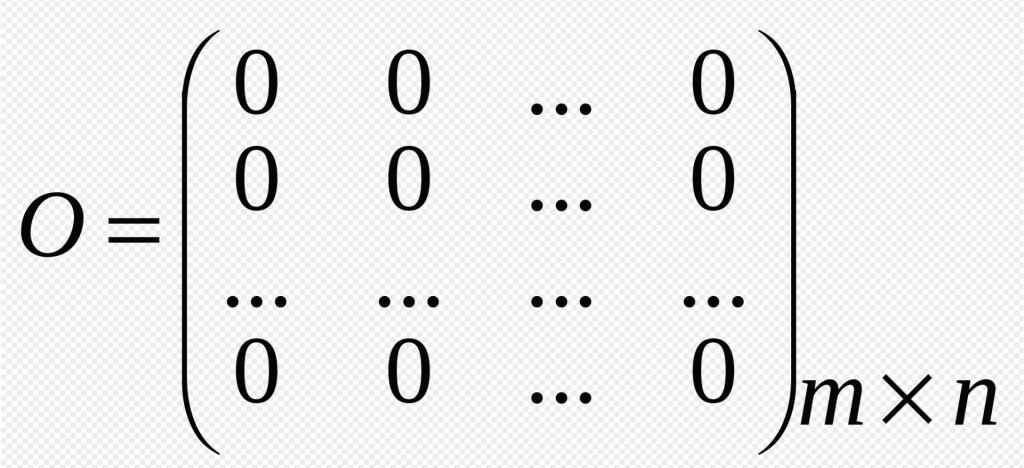
• Нулл матрик Овај облик постоји када су сви његови елементи једнаки 0. Означавају овај тип матрице "О" Овај елемент је добио и име због чињенице да у рачуници има сличне функције са нулом у теорији бројева.
• Скуаре. Овај тип матрице је најчешћи, његова разлика је у томе што има једнак број колона и редова. Када су два елемента повезана на различитим крајевима колоне, добијамо главну дијагоналу. У том смислу, дијагонална табела је подељена на неколико система:

а) Дијагонала. Овај тип квадратне матрице, који не укључује елементе који припадају главној дијагонали.

б) Сингле. Овај тип дијагонале се састоји само од једне јединице. За све ово, свака таква матрица је скаларна.

ц) Скалар. Ово је тип где се главна дијагонала састоји од истог броја.

д) Стрелица. Ово је врста квадратне матрице у којој су скоро сви елементи нула, али компоненте које чине прву колону, као и оне које се односе на дијагоналу и први ред, нису једнаке њој.

• Бинари Овај тип табеле се састоји од нула и јединица.
• Пасцалова матрица - у овој врсти матрице сви елементи се састоје од бројева који припадају истом имену.
• Тридиагонал У овој врсти матрице, нулти елементи се налазе на три дијагонале, које укључују главну и оне изнад и испод.

Матрица ранга

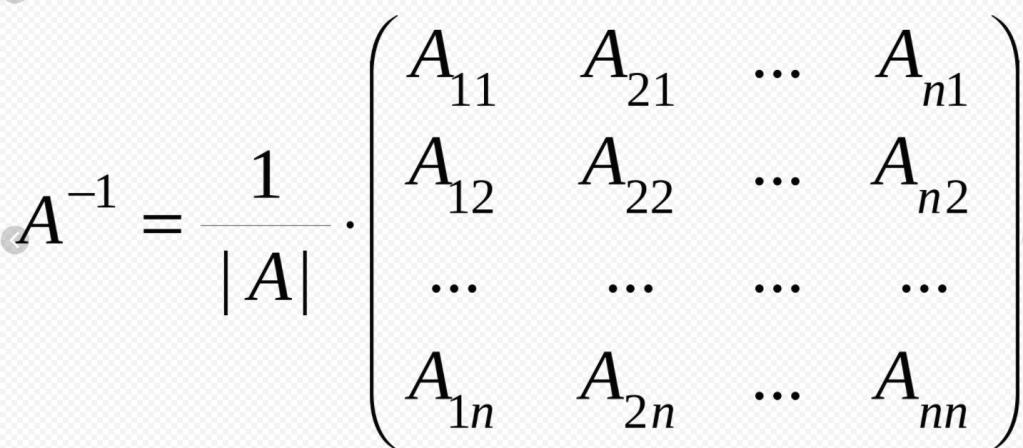
Сазнавши да има различите типове, потребно је рећи о сљедећем концепту: ранг матрице. Под овим се подразумева број независних линеарних колона или број независних линеарних редова. Такође, ранг било које матрице је редослијед малолетника, који је највиши, његова детерминанта је нула.

Ранг је означен рангом А, али се налази ранг А. Оба концепта се сматрају исправним, тако да се са различитим правописима то неће сматрати грешком. Главно је не заборавити да је ред редова увек једнак рангу колона.

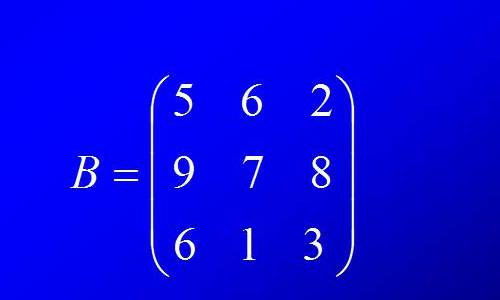
Акције на матрици

Матрица је универзални систем за решавање алгебарских проблема, на њему се изводе различите акције. То укључује умножавање двије матрице, збрајање, множење бројем и друге матрице.

Извођење бројних акција у алгебри, систем различитих матрица помаже да се пронађе лакши начин за решавање проблема. Потребно је мање времена и помаже да се не изгубите у многим акцијама.

Операције повезане са матрицом користе се не само у математици, већ иу физици и хемији.