Стабло одлука је примјер. Методе доношења одлука

У већини случајева, одлучивање се може обавити брзином муње, на основу нашег искуства, како кажу, оком. Али понекад се ова опција не сматра адекватном. И шта да радимо у овом случају? Посебно за ове паметне људе развијене су методе доношења одлука. Омогућавају постепено и са минималним одступањима да разраде алгоритам акција.

Опште информације

А најзанимљивији тренутак за нас је метода стабла одлучивања. Какав је он? Где се користи? Метод стабла одлучивања је графички приказ одређених акција и стања окружења који указују на одговарајуће вероватноће и добитке за одређене комбинације. Користи се за процјену ризика пројеката, када је потребно уложити средства за значајан временски период. Разлог за његово коришћење је имати два или више узастопних скупова решења. И они би требало да теку из претходног и / или скупа стања околине.

О формалној структури

Који се елементи користе за креирање? Ово је:

1. Солутион ноде. Користи се за карактеризацију тренутка избора.
2. Линија која представља алтернативу.
3. Чвор догађаја Користи се за означавање одређене случајности која се дешава.
4. Линија која описује окружење које је резултат непредвиђеног догађаја.
5. Резултат чвор. Користи се за означавање укупних износа. Она је повезана са специфичним стањем околине и одлукама.
6. Ноде да означи средњи резултат. Неопходно је указати на ситуацију када треба донијети другу одлуку.

Изградња

Како се метод стабла одлучивања користи у пракси? Да би се формулисали различити сценарији развоја, неопходно је имати све потребне и поуздане информације, које узимају у обзир вјероватноће и вријеме настанка одређених догађаја и резултата. У почетку се прикупљају подаци. Да бисте то урадили, можете користити следећи алгоритам:

1. Одређује се састав и трајање фаза животног циклуса;
2. Предвиђени су кључни догађаји који ће утицати на (или можда промијенити) даљи развој;
3. Утврђује се вријеме њиховог појављивања;
4. Формулисана су сва могућа решења која се разматрају као опције за кључне догађаје;
5. Утврђује се вјероватноћа њиховог усвајања;
6. Процењени трошкови фаза у текућим ценама.

На добијеним подацима, сасвим је могуће да се направи стабло одлучивања. Она ће садржати чворове који се сматрају кључним догађајима. У суштини, то су тачке одлучивања. Њима се придружују гране - то јест, одређени радови који имају за циљ постизање одређеног резултата. Израда стабла одлучивања омогућава вам да израчунате вероватноћу за сваки изабрани сценарио. Поред тога, пажња се посвећује и другим фундаментално важним показатељима који су неопходни за анализу ризика и усвајање ефективних управљачких активности. Треба напоменути да се овај метод обично користи за пројекте који имају више могућих опција. Заиста, у супротном, схема постаје сувише обимна, што отежава израчун оптималног рјешења и одабир потребних података. Разумијевање како да се направи дрво одлука треба већ да се формира. Погледајмо примере.

Инвестициони пројекти

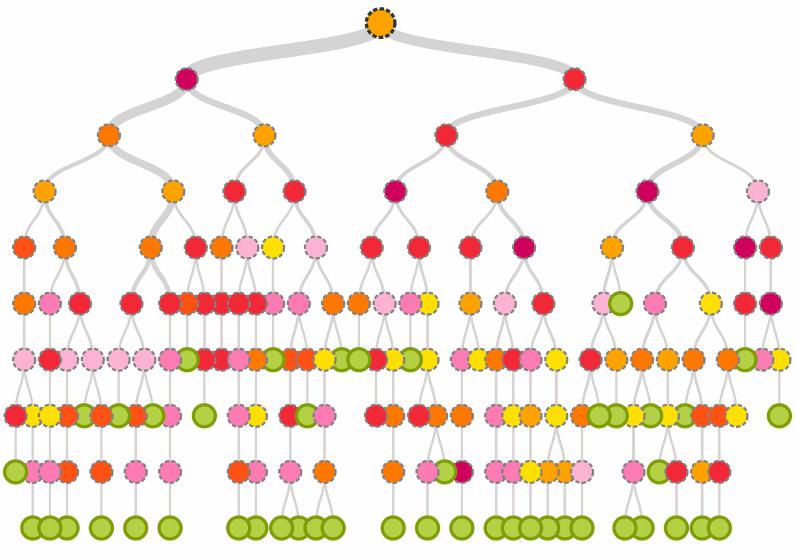
Најбољи начин да се разјасни дрво одлука је примјер из живота. Зато је боље почети са њом, а не са апстрактном математиком. Претпоставимо да имамо избор од три инвестициона пројекта. Означавамо их као ИП1, ИП2 и ИП3. Претпоставимо да је за њихову имплементацију потребно уложити 200, 300 и 500 милиона рубаља. Очекивани профит је 100, 200 и 300 милиона рубаља. Постоји ризик од губитка новца. Вероватноћа таквог сценарија је 10%, 5% и 20% за сваку од опција. Шта је боље изабрати? Проналажење чисто математичког одговора је веома тешко. Али са употребом стабла одлучивања, овај задатак је много лакши. У почетку је потребно направити дрво одлуке о инвестиционом пројекту. Након што је изграђена, почињемо да је истражујемо помоћу обрнуте анализе. Морате отићи на слику с десна на лијево. Ући у круг, морамо у њих ставити математичке вриједности очекивања плаћања. У нашем случају, резултат ће изгледати овако:

1. 100 * 0,9 - 200 * 0,1 = 70;
2. 200 * 0.95 - 300 * 0.05 = 175;
3. 300 * 0.8 - 500 * 0.2 = 140.

На основу калкулација, лако је видети да је ИП2 најповољнији за нас. А сада хајде да заронимо у математику и размотримо неке апстрактне проблеме на стаблу одлучивања.

Најједноставнији примјер

У овом случају, ми ћемо имати само две опције - „не“ или „да“. Или, на језику логичке логике, ми ћемо имати 0 или 1. Разумевање таквог примера стабла одлучивања може бити тешко, тако да ћемо користити “не” или “да”. Претпоставимо да нам је понуђено да радимо за 160 рубаља на сат. Можемо рећи не, и онда се ништа неће промијенити. Или кажемо “да”, а онда, пошто смо мало радили, можемо да осетимо како је у нашем џепу постао тежи за 160 рубаља. Можете мало комплицирати модел, ау случају договора додати наставак. На пример - напорно радите? Ако “да”, онда плаћање 300 рубаља, ако “не”, онда остајемо на истом нивоу од 160.

Разрада стратегија животног понашања

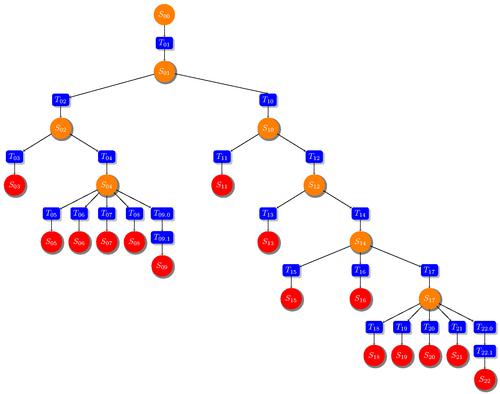
Многима се може чинити да се примјер стабла одлучивања користи само за велика улагања и апстрактна математичка истраживања. Али није. Наравно, можете запамтити теорију. И можете га усвојити и победити. А сада ћемо погледати формулу коју је Јеан-Паул Гетти предложио, под називом "Како постати богат". Кратко се изражава: "Устани рано", "Напорно ради", "Нађи уље". Погледајмо моделирање низа одлука:

1. Морамо да бирамо између "Устај рано" и "Спавај касно". Ово је најједноставнији избор.
2. Морамо да бирамо између “Радимо напорно” и “После рукава”. Ово је и најједноставнији избор.
3. Истовремено, догађај "Пронађено уље" може се појавити са одређеном вјероватноћом. Његова вредност зависи од редоследа наших одлука.

Ако пронађемо уље, онда смо постали богати. Нема пронађених депозита - то значи да постоје само губици, потрошња на претрагу. А ако спавате касно и радите безбрижно, онда не можете чак ни тражити нафту. Највише преферирана опција је “Устани рано” и “Напорно ради”.

Тражимо нашу нафту

А сада за калкулације. Разматрани пример стабла одлучивања боље је објаснити помоћу табела. Претпоставимо да радимо оптимално. Онда наша опција:

Као што видите, најпрофитабилнија опција нуди прилично добре изгледе. Да ли је могуће да се ова табела користи у потпуности да би се могао видети овај пример? Да, и то није тако тешко као што се чини на први поглед:

Овај примјер стабла одлучивања јасно нам показује да је кључ успјеха тежак посао. Величина радног дана може нас приближити циљу да постанемо богати и повећамо величину државе. Иако су, наравно, подаци овде прилично генерализовани, али се надамо да је општи ток мисли разумљив.

Побољшање примера

Неко се може расправљати - добро, стабло одлука је корисно. Но, разматране опције су превише претјеране, а њихово кориштење у стварној ситуацији је прилично проблематично. Ово мишљење има право да постоји, али само за оне који нису разумели. Стабло одлучивања може бити веома сложено и флексибилније. Стога ћемо мало побољшати нафтни примјер. И овај пут морамо узети у обзир повратак. Претпоставимо да се средства за потрагу за нафтом троше одмах. Ако нађемо минерал, све инвестиције које су направљене у истраживању одмах ће се исплатити. Приходи ће доћи за двије године. Као што видите, имамо рачуне и исплате које су расуте током временског периода. И морамо да донесемо све износе на расположиви новац. Претпоставимо да је дисконтна стопа 20%, онда ће наша формула за особу која напорно ради и рано устати изгледати овако: (0.1 * 10 000 000) / 1.22 + 0.9 (-200 000) = 514 444. За остале варијанте активности, вредности ће бити: 157,222, - 128,555, и - 200,000 рубаља. Слажем се, ово је више као образложење за пројекат! Упркос чињеници да су се нивои прихода смањили, још увијек је најефикаснија могућност напорног рада и раног устајања. Онда, како касно спавати, не привлачи. И шта је доношење одлука корисно за нас, како у животу, тако иу калкулацијама?

Пример загрејте

Нудимо читатељима да обједине своје знање. Претпоставимо да имамо доктора. Он производи производе П1 у износу од хиљаду јединица. Шеф ДОК-а сматра да се тржиште за робу П2 шири. Спроведене су студије које су омогућиле утврђивање предложених развојних опција: П1мак = 1000; П1мин = 5000; П2мак = 8000; П2мин = 4000. Овде мин и мак је вероватноћа потражње за одређеном количином робе. То је, хиљаду П1 није проблем за имплементацију. Али 5000 можда неће моћи. Вероватноћа тражње је: Ц1мак = 0,7; Ц1мин = 1-Ц1мак = 0,3; С2мак = 0,6; Ц2мин = 1 - Ц2мак = 0.4. По јединици робе П1 остварујемо профит у износу од 1 новчане јединице. За А2, ова бројка је 0.9. Али постоји проблем - минимална потражња за оба производа надмашује постојеће и расположиве капацитете МКЛ-а. Који ће бити трошкови (сада једнаки К) да би се удвостручили за паралелну производњу у еквиваленту, ако:

1. трошкови су К = 0,4 * 103 монетарне јединице;
2. еквивалентна количина П1 = 1000, и П2 = 900;
3. максимална и тренутна потражња за П1 и П2 су: (К1мак = 2 * 103; К1мин = 1.4 * 103) и (К2мак = 1.2 * 103; К2мин = 0.8 * 103).

Имајући такве податке, потребно је одредити да ли је препоручљиво замијенити произведене производе и развити капацитете.

Решавање проблема

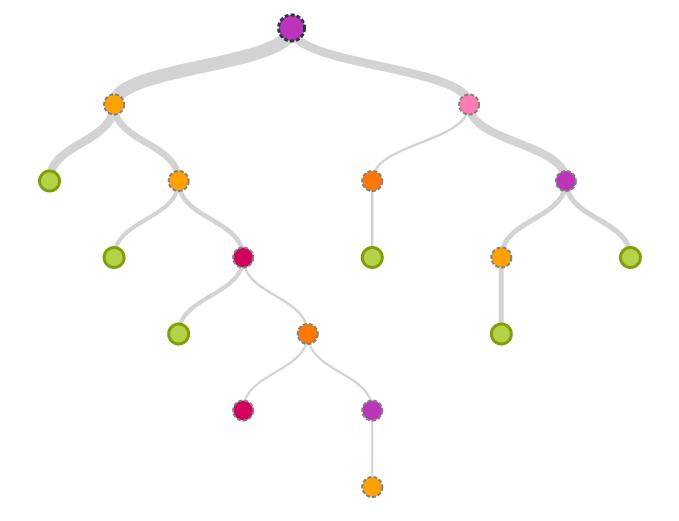
Да ли је тешко сами то схватити? Па, мали савет - можете користити алгоритам који је коришћен у примеру са уљем. За оне који то не могу, биће написано решење. У почетку утврђујемо последице наших одлука за производњу једног типа (П1 или П2). Затим истражите опцију са оба. Да бисмо то учинили, одбацујемо ирационалне акције за развој капацитета и издвајамо податке о могућим добитцима одвојено у колони. Ми узимамо у обзир вероватноћу тражње и процењујемо просечну ефикасност у гранама. Ако израчунамо, видећемо да је са продуженом производњом П1 производа, корисније за нас у развоју капацитета и истовремене производње од преласка на један П2. Иако је то минимална очекивања. А шта је са максималном потражњом? У овом случају, треба да нацртамо другу грану која ће размотрити ово решење. Да бисмо израчунали његову ефикасност, сумирамо прву и другу опцију и одузимамо трошкове удвостручења капацитета. И испоставило се да је ово најпрофитабилније рјешење. Као резултат тога, долазимо до закључка да је потребно развити капацитете и осигурати истовремено ослобађање П1 и П2.

Постављање циљева

То је оно што је дрво одлука. Примери решавања проблема ризика нам омогућавају да разумемо овај метод и да га усвојимо. Наравно, у почетку могу постојати одређене потешкоће, али се они успјешно рјешавају праксом. У томе могу помоћи књиге из математике, економетрије, кибернетике и бројних других дисциплина.

Способност аутоматизације

Методе одлучивања имају јасну структуру. Дакле, компјутерске технологије могу врло лако радити с њима. Као још један примјер, процес издавања кредита у банци. Истовремено, за компјутер, стабло одлучивања је представљено у облику логичког конструкта "ако ... онда ...". Иако је, узгред речено, заснован на овом принципу и за људе, али када је у интеракцији са технологијом, потребно је да се пажња усредсреди на то. Претпоставимо да је први корак питање старости. Ако је особа млађа од четрдесет година, онда питају за његово образовање и наднице. Још - има ли куће. Одговор је да - издајемо кредит. Негативно - питајте о нивоу прихода. Мање од 20 хиљада рубаља месечно - ми одбијамо. Ово се ради брзо и ефикасно.

Закључак

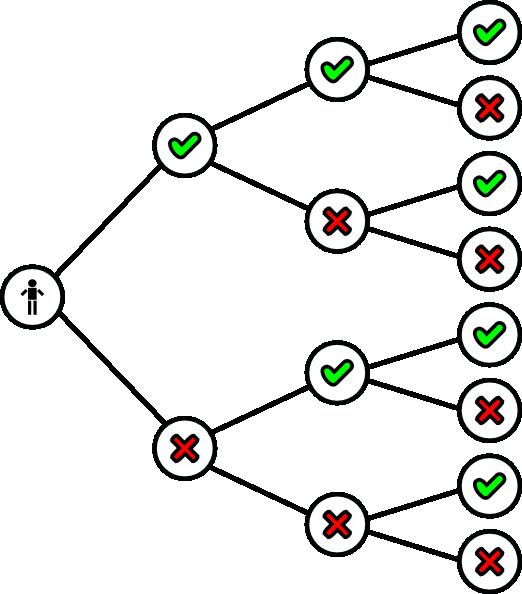
Ако постоји неколико понашања и сценарија, онда бисте требали користити дрво одлука да бисте пронашли најбољу ситуацију. То ће омогућити стављање свих доступних информација и калкулација на папир и побољшати ефикасност доношења одлука.