Закон рефракције светлости: формулација и практична примена
Феномен преламања светлосног таласа схвата се као промена у правцу ширења фронта овог таласа док пролази из једног прозирног медија у други. Многи оптички инструменти и људско око користе овај феномен за обављање својих функција. У чланку се разматрају закони преламања светлости и њихова употреба у оптичким уређајима.
Процеси рефлексије и преламања светлости
С обзиром на питање закона преламања светлости, потребно је поменути феномен рефлексије, јер је уско везан за овај феномен. Када светлост прође из једног прозирног медија у други, онда се на интерфејсу ових медија одвијају два процеса истовремено:
- Део светлосног снопа се рефлектује назад на први медиј под углом који је једнак куту упада иницијалне греде на интерфејс.
- Други дио снопа улази у другу околину и наставља се ширити у њему.
Горе наведено указује да ће интензитет иницијалног снопа светлости увек бити већи од интензитета рефлектоване и преламане светлости одвојено. Како се тај интензитет расподјељује између снопова овиси о својству медија и куту упадања свјетла на граници.
У чему је суштина процеса преламања светлости?

Дио снопа свјетлости који пада на површину између два прозирна медија наставља се ширити у другом медију, али ће се смјер његовог ширења већ разликовати од изворног смјера у 1. медију под одређеним кутом. Ово је феномен преламања светлости. Физички узрок ове појаве је разлика у брзини ширења свјетлосног вала у различитим срединама.
Подсјетимо се да свјетлост има максималну брзину ширења у вакууму, једнака је 299,792,458 м / с. У сваком материјалу, ова брзина је увек нижа, и што је већа густина медија, то се електромагнетски талас шири у њему. На пример, у ваздуху, брзина светлости је 299,705,543 м / с, у води на 20 ° Ц већ 224,844,349 м / с, ау дијаманту она пада више од 2 пута у односу на брзину у вакууму, и износи 124,034,943 м / с.
Хуигенс принцип
Овај принцип обезбеђује геометријску методу за проналажење фронта таласа у било ком тренутку. Принцип Хуигенса претпоставља да је свака тачка до које валовити фронтови извор електромагнетних секундарних таласа. Шире се у свим правцима истом брзином и фреквенцијом. Резултујући таласни фронт дефинисан је као скуп фронтова свих секундарних таласа. Другим речима, фронт је површина која додирује сфере свих секундарних таласа.
Демонстрација употребе овог геометријског принципа за одређивање фронта таласа приказана је на доњој слици. Као што се може видети из ове шеме, сви радијуси сфера секундарних таласа (приказани стрелицама) су исти, јер се предњи талас шири у хомогеном медијуму са оптичке тачке гледишта.
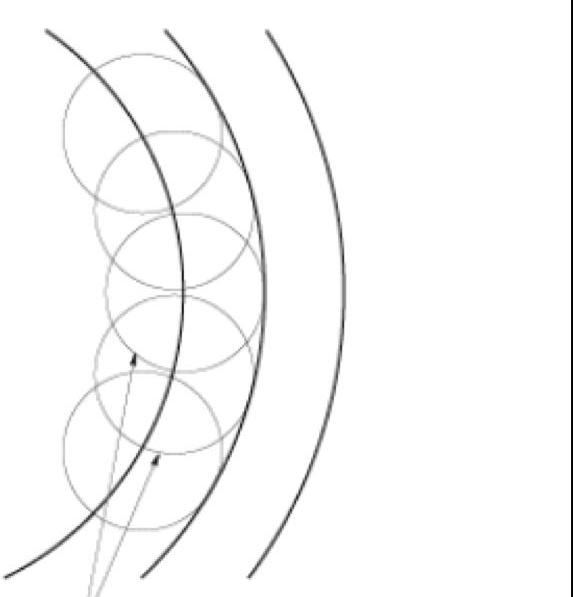
Примена принципа Хуигенса на процес преламања светлости
Да бисмо разумели закон преламања светлости у физици, можемо користити принцип Хуигенса. Размотримо неки светлосни ток који пада на граници између два медија, а брзина кретања електромагнетног таласа у првом медију је већа од брзине за други.
Чим део фронта (лево на слици испод) дође до раздвајања медија, у свакој тачки површине интерфејса почињу да се побуђују секундарни сферни таласи, који ће се већ ширити у другом медију. Пошто је брзина светлости у другом медију мања од ове вредности за први медиј, део фронта који још није достигао интерфејс између медија (десно на слици) наставиће да се шири већом брзином од оног дела фронта (лево) који је већ ударио у други медиј . Цртање кругова секундарних таласа за сваку тачку са одговарајућим радијусом једнако в * т, где је т одређено специфично време ширења секундарног таласа, и в је брзина његовог ширења у другом медију, а затим цртање тангентне криве на све површине секундарних таласа ширење светлости у другом окружењу.
Као што се може видети из слике, овај фронт ће бити скренут под неким углом од почетног правца његовог ширења.
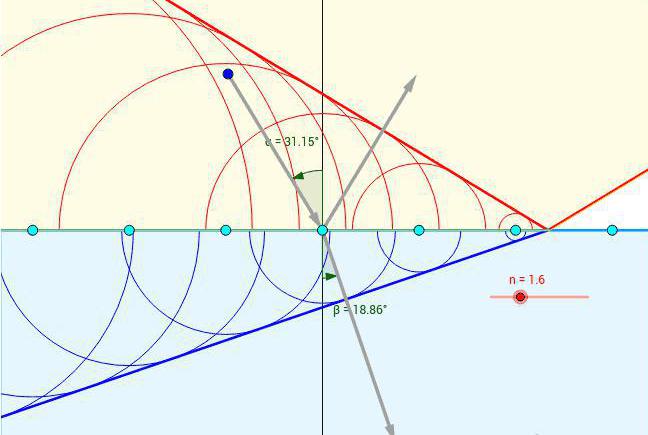
Треба приметити да ако су брзине таласа биле једнаке у оба медија, или ако је светлост пала окомито на интерфејс, онда не би могло бити говора о процесу рефракције.
Закони рефракције светлости
Ови закони су добијени експериментално. Нека су 1 и 2 два прозирна медија, а брзине ширења електромагнетних таласа су в 1 и в 2 . Нека сноп светлости падне на интерфејс од средине 1 под углом θ 1 до нормале, ау другом медију наставља да се шири под углом θ 2 у односу на нормалну границу. Тада ће формулација закона рефракције светлости бити следећа:
- У истој равнини бит ће двије греде (инцидентне и ломљене) и нормално враћена на међусклоп између медија 1 и 2.
- Однос брзина ширења снопа у медијима 1 и 2 биће директно пропорционалан односу синуса углова упадања и рефракције, тј. Син (θ 1 ) / син (θ 2 ) = в 1 / в 2 .
Други закон се зове Снеллов закон. Ако узмемо у обзир да је индекс или индекс преламања прозирног медија дефинисан као однос брзине светлости у вакууму према тој брзини у медијуму, тада се формула за закон преламања светлости може преписати као: син (θ 1 ) / син (θ 2 ) = н 2 / н 1 , где су н 1 и н 2 индекси преламања медија 1 и 2, редом.
Дакле, математичка формула закона показује да је производ синуса кута и индекс преламања за одређени медиј константна вредност. Штавише, узимајући у обзир тригонометријска својства синуса, можемо рећи да ако је в 1 > в 2 , онда ће се светлост приближити нормалном приликом проласка кроз интерфејс и обрнуто.
Кратка историја открића закона

Ко је открио закон преламања светлости? У ствари, први пут је то формулисао средњовековни астролог и филозоф Ибн Сахл у 10. веку. Секундарно откриће закона догодило се у 17. стољећу, а то је учинио низоземски астроном и математичар Снелл ван Роиен, тако да други свјетски закон лома носи његово име.
Интересантно је напоменути да је мало касније овај закон отворио и Француз Рене Десцартес, па у француским земљама он носи своје име.
Пример задатка

Сви проблеми закона преламања светлости заснивају се на математичкој формулацији Снелловог закона. Да наведемо пример таквог задатка: потребно је да се приликом његовог преласка из дијаманта у воду нађе угао ширења фронта светлости, под условом да овај фронт падне на интерфејс под углом од 30 о у односу на нормалу.
Да би се решио овај проблем, неопходно је знати или рефракцијске индексе разматраног медија или брзину ширења електромагнетског таласа у њима. Позивајући се на референтне податке, можемо записати: н 1 = 2.417 и н 2 = 1.333, где бројеви 1 и 2 означавају дијамант и воду.
Замењујући добијене вредности у формулу, добијамо: син (30 о ) / син (θ 2 ) = 1,333 / 2,417 или син (θ 2 ) = 0,39 и θ 2 = 65,04 о , тј.
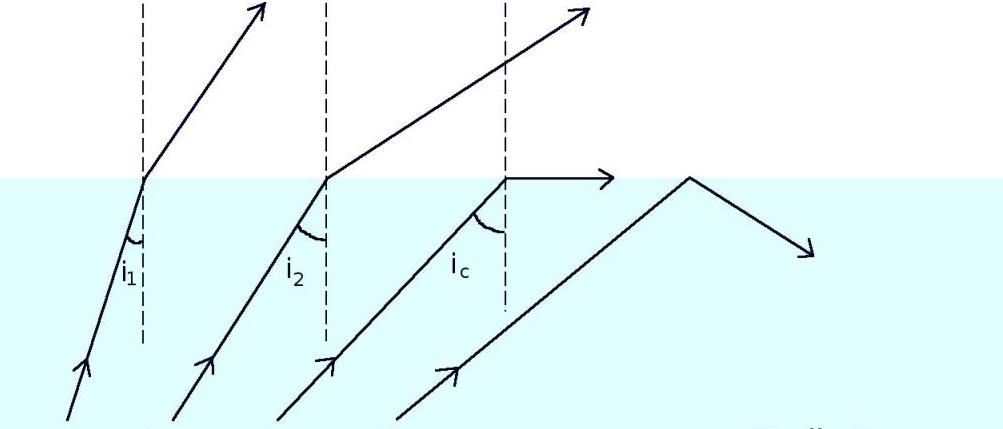
Интересантно је приметити да, ако је угао упадања био већи од 33,5 о , онда, у складу са формулом закона преламања светлости, не би постојао рефракциони зрак, а цео фронт светлости би се рефлектовао натраг у дијамантни медиј. Овај ефекат је у физици познат као потпуна унутрашња рефлексија.
Где се примењује закон преламања?
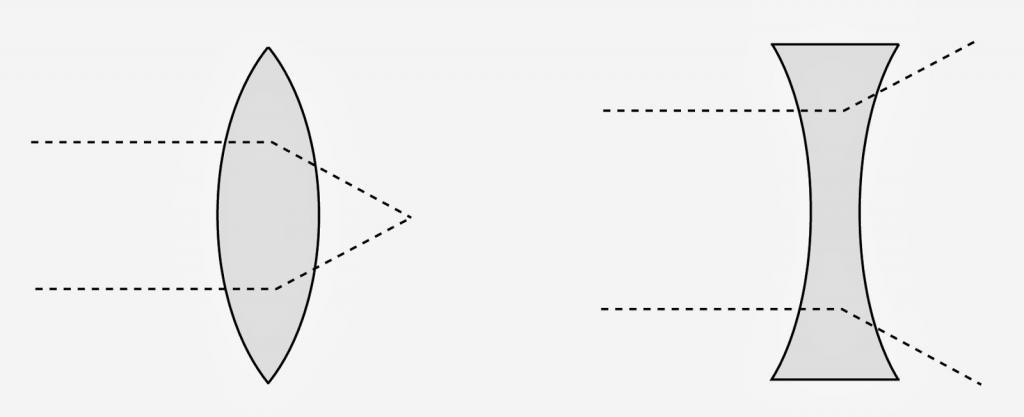
Практична примена закона лома светлости је различита. Може се без претјеривања рећи да већина оптичких уређаја ради на овом закону. Рефракција светлосног флукса у оптичким објектима се користи у уређајима као што су микроскопи, телескопи и двогледи. Без постојања рефрактивног ефекта, било би немогуће да особа види свет око себе, јер је стакласто тело и сочиво ока биолошка сочива која обављају функцију фокусирања светлосног тока на тачку на осетљивој мрежници ока. Поред тога, закон укупне унутрашње рефлексије налази своју примену у светлим влакнима.