Периметар квадрата и правоугаоника. Методе одређивања и примери решења.

Често, на Интернету, можете наћи исмевање о томе како знање математике - интеграли, диференцијали, тригонометријске функције и други делови теме - не помажу да се олакша живот особе. Такви вицеви су узалудни, јер као што помаже способност исправног израчунавања обима квадрата, правокутника и других геометријских облика у грађевинским радовима. Потрошња материјала: плочице, тапете, подови - не могу се одредити без разумевања основних математичких формула и геометријских облика.

Скуаре пропертиес

Било какви прорачуни у математици су засновани на својствима објекта. Да би се одговорило на питање: "Шта је периметар квадрата?" - препоручује се да се присетимо карактеристичних карактеристика ове фигуре.

1. Једнакост свих страна.
2. Присуство четири угла од 90 степени.
3. Паралелност странака.
4. Пивот симметри. Када се бројка окрене, њен изглед остаје непромењен.
5. Способност да се опише и уђе у круг.
6. Дијагонале на раскрсници се дијеле на пола.
7. Подручје слике карактерише простор испуњен квадратом у дводимензионалном простору.
8. Периметар фигуре није ништа друго до сума дужина његових страна.
9. Из претходног својства произилази да ће јединице мјерења периметра бити јединице дужине: м, цм, дм и друге.

Да бисте пребројали подне даске да завршите поправке у квадратној соби, морате знати дужину просторије. Да бисте то урадили, израчунајте његов периметар.

Периметар

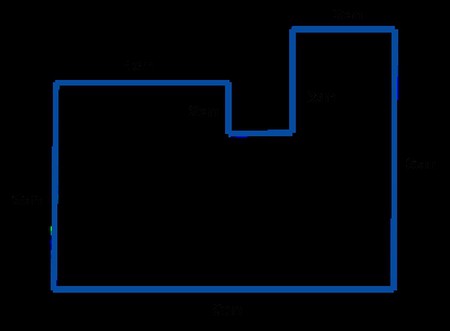
Преведено са грчке ријечи значи "мјерити около". Термин се односи на све затворене облике: квадрат, круг, правоугаоник, троугао, трапез и друге. Познавање дефиниције периметра елементарних фигура неопходно је за рјешавање сложених геометријских проблема с објектима неправилног облика. На пример, да бисте израчунали постоља у просторији са распоредом типа „Г“, или како се још назива „боот“, биће потребно одредити обим квадрата и правоугаоника. Уосталом, облик просторије се састоји од ових елементарних фигура.

Стандардна ознака такве величине је слово Р. Свака фигура, узимајући у обзир њена својства, има своју формулу за одређивање периметра.

Рецтангле пропертиес

1. Једнакост супротстављених страна.
2. Једнакост дијагонала.
3. Способност описивања круга.
4. Висине правоугаоника једнаке су његовим странама.
5. Зброј углова је 360 степени, а сви углови су у праву.
6. Паралелност супротних страна.
7. Перпендикуларност суседних страна.
8. Збир квадрата дијагонала правоугаоника једнак је збиру квадрата његових страна.
9. Пресијецају се дијагонале које се дијеле на пола.
10. Немогућност уклапања круга у облик.

Периметрал скуаре

У зависности од утврђених (познатих) параметара квадрата постоје различите формуле за одређивање његовог периметра. Једноставан задатак је израчунати периметар на фиксној дужини његове стране. У овом случају, Р = с + с + с + с или 4 * с. На пример, дужина стране квадрата је 7 цм, а периметар фигуре ће бити 28 цм (4 * 7).

У првом случају, све је јасно, али како пронаћи периметар квадрат, знајући његову област? И овде је све јасно. Пошто се површина фигуре одређује множењем једне стране са другом, а све стране су једнаке на квадрату, потребно је издвојити корен из познате вредности. Пример: постоји квадрат са површином од 25 дм ² . Коријен од 25 је 5 - ова вредност карактерише дужину стране квадрата. Сада, замењујући пронађену вредност - 5 дм ² - оригиналној периметричној формули, можемо решити проблем. Одговор ће бити 20 дм. То је, 4 помножено са 5, добило жељену вредност.

Квадрат и круг

Из својстава разматране фигуре изгледа да се круг може уписати у квадрат и описати око фигуре.

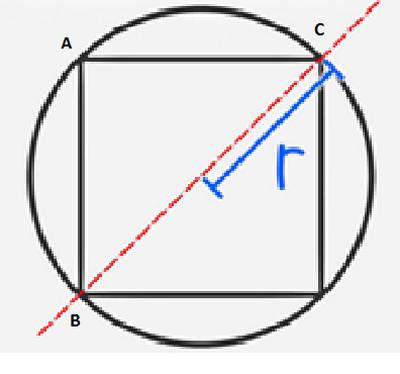
Прва опција је пронаћи периметар дуж обода кружнице. Уписан је квадрат чији су врхови на кружници. Полупречник круга је 1/2 дијагоналне дужине. Испада да је пречник једнак дијагонали. Сада морате размотрити правоугаони троугао што је резултат подјеле дијагонале квадрата. Рјешење проблема своди се на проналажење страна овог трокута. БЦ је позната вриједност, промјер кружнице. Претпоставимо да је једнак 3 цм, Питагорина теорема у случају једнаких страна троугла ће изгледати овако: 2ц ² = 3 ² . У формули, симбол с је дужина стране троугла и квадрата; 3 - позната вредност хипотенузе. Дакле, ц = /9 / 2. Знајући страну трга, његов обим није проблем за израчунавање.

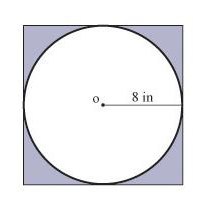
Карактеристика уписане кружнице је подјела страна квадрата на пола. Према томе, радијус је једнак половини дужине стране квадрата. Затим страна ц = 2 * радијус. Периметар квадрата у овом случају је 4 * 2 * радијуса или 8 полупречника круга.

Периметријски правоугаоник

Најосновнија формула за одређивање периметра правоугаоника кроз познате вредности његових страница је следећа: П = 2 (а + б), где су а и б дужине страна фигуре.

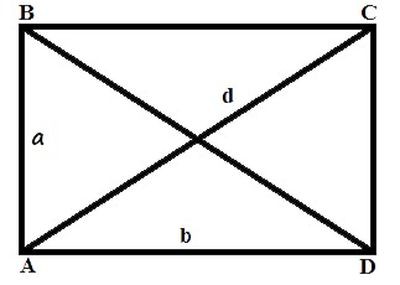
Дијагонала правоугаоника, слично квадрату, дели фигуру на пола, формирајући правоугаони троугао. Међутим, задатак се компликује чињеницом да су стране овог трокута неуједначене. У случају познате вредности једне од страна и дијагонале, друго се може наћи следећи Питагорину теорему: д ² = а ² + у ² , где су а и в стране фигуре, а д је дијагонала.

Ако ниједна од странака није позната, тада долази до знања о тригонометрији: синусима, косинусима и другим функцијама.

Проналажење периметра дуж описне кружнице и познатог пречника своди се на чињеницу да је пречник једнак дуљини дијагонале слике. Даље, решење проблема се одређује присуством познатих количина. Ако су дати углови, онда кроз тригонометријске функције. Ако је једна страна дата, одговор ће се наћи кроз Питагорину теорему.

Правоугаоник и тригонометријске функције

Ради јасноће, пример решавања проблема. Гивен: рецтангле АВСД; дијагонална дужина ( д ) 20 цм; угао ф - 30 °. Нађите периметар фигуре.

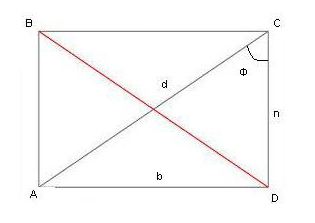
Из тригонометрије је неопходно да се присетимо следећег: синус угла у правоугаоном троуглу једнак је односу супротне ноге на хипотенузу. Синус од 30 ° (постоје табеле по којима се могу одредити вредности тригонометријских функција за исправне углове) је 1/2. Испада 1/2 = однос у д . Непозната вредност у ће бити једнака д / 2 = 20/2 = 10 цм.

Да бисте израчунали периметар, требало би да нађете другу страну слике. То је могуће захваљујући Питагориној теореми, јер су дужине хипотенузе и једне од ногу познате, или опет кроз однос аспеката за косинус кута.

Косинус кута ас је изражен као однос суседног крака према хипотенузи и једнак је /3 / 2.

/3 / 2 = н / д , н = (д * )3) / 2 или 10 * .3. Након вађења корена из 3, добијамо дужину стране троугла: 10 * 1,73 = 17,3 цм.

Периметар је 2 (17.3 + 10) = 2 * 27.3 = 54.6 цм.

Периметар и однос

У школском програму постоје проблеми у геометрији, када се дужине страна правокутника изражавају њиховим међусобним односом. Разматрање решења овог проблема представљено је у наставку.

Познато је да је збир дужина свих страна правокутника, односно његовог периметра, 84 цм, а однос дужине (д) према ширини (в) је 3: 2. Нађите стране фигуре.

Решење: нека је дужина 3к, а ширина 2к, према односу из стања проблема. Формула периметра правоугаоника са подацима дужина страна биће следећа: 3к + 3к + 2к + 2к = 84. Надаље, 10к = 84, к = 8,4 цм, замјеном к у израз дужине и ширине правокутника, можете пронаћи жељене вриједности. Дужина ће бити: 3 * 8.4 = 25.2 цм; ширина: 2 * 8,4 = 16,8 цм.

Чланак је посвећен рјешавању најчешћих задатака у школском програму. И то нису сви начини проналажења периметра квадрата и правоугаоника.