Волумен конуса, његов израчун

Геометрија као наука формирана је у древном Египту и достигла висок ниво развоја. Познати филозоф Платон основао је Академију, у којој је велика пажња посвећена систематизацији постојећег знања. Цоне као један од геометријски облици први пут се спомиње у чувеној расправи Еуклида "Почетак". Еуклид је био упознат са Платоновим дјелима. Сада мало људи зна да реч "конус" у преводу са грчког значи "боров конус". Грчки математичар Еуклид, који је живео у Александрији, сматра се оснивачем геометријске алгебре. Стари Грци не само да су постали насљедници Египћана, већ су и увелико проширили теорију.

Историја дефиниције конуса

Геометрија као наука настала је из практичних захтева конструкције и посматрања природе. Постепено, експериментално знање је генерализовано, а својства неких тела доказана су кроз друге. Стари Грци су увели концепт аксиома и доказа. Аксиом је изјава добијена на практичан начин и не захтева доказ.

У својој књизи, Еуклид је навео дефиницију конуса као лик, који се добија ротацијом правоугаоног троугла око једне од ногу. Он такође поседује главну теорему која одређује запремину конуса. А ову теорему је доказао стари грчки математичар Еудокс из Книда.

Други математичар античке Грчке, Аполоније од Перг, који је био ученик Еуклида, развио је и изложио теорију коничних површина у својим књигама. Припада дефиницији коничне површине и секанту према њој. Школарке нашег дана проучавају еуклидску геометрију, која је од античких времена сачувала главне теореме и дефиниције.

Основне дефиниције

Прави кружни конус се формира ротирањем правог троугла око једне ноге. Као што се може видети, конус се није променио од дана Еуклида.

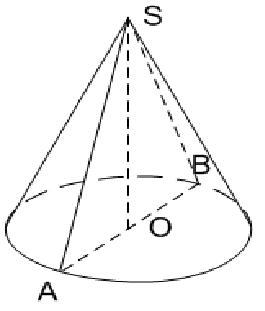
Хипотенуса АС правоугаони троугао АОС, када се ротира око ногу ОС-а, формира бочну површину конуса, па се назива генератрик. Нога ОС троугла се истовремено претвара у висину конуса и његову ос. Тачка С постаје врх конуса. Цатет АО, описујући круг (база), претворен у радијус конуса.

Ако је раван повучена од врха кроз врх и ос конуса, онда можете видети да је резултујући аксијални пресек једнакокрачан троугао, у коме је оса висина троугла.

Такође је често потребно израчунати бочну површину тијела револуције. Површина бочне површине конуса је једнака продукту од половине дужине обима базе и генерише конуса.

С = Ц * Л / 2 = н * Р * Л / 2

где је Ц обим базе, л је дужина генеруса конуса, Р је основни радијус.

Формула за израчунавање волумена конуса

Следећа формула се користи за израчунавање запремине конуса:

В = С * Х / 3,

где је С површина базе конуса. Пошто је база круг, њена површина се израчунава на следећи начин:

С = нР ² .

Следи:

В = н * Р ² * Х / 3,

где је В запремина конуса;

н је број једнак 3.14;

Р је основни радијус који одговара сегменту АО на Слици 1;

Х - висина једнака сегменту ОС.

Волумен обрушеног конуса

Постоји раван кружни конус. Ако је равнина окомита на висину, одсећи горњи дио, добивате скраћени конус. Две базе су кружног облика са полупречницима Р1 и Р2.

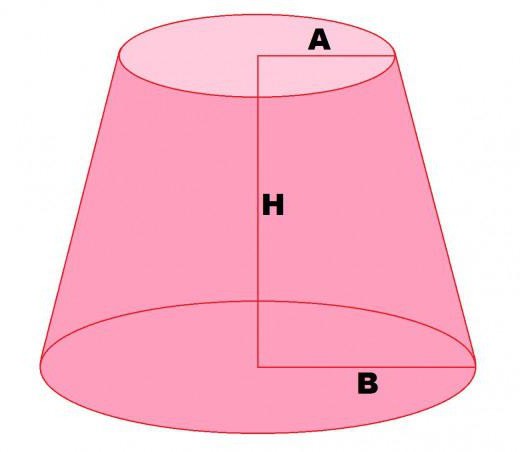
Р1 = А;

Р2 = Б;

Х = Х.

Ако се прави конус формира ротирањем правог троугла, онда се крњи конус ротира. рецтангулар трапезоид око равне стране.

Обим пресјеченог стошца се израчунава по следећој формули:

В = н * (Р ₁ ² + Р ₂ ² + Р ₁ * Р2) * Х / 3.

Конус и његов део авионом

Древни грчки математичар Перу Аполоније од Пергског припада теоретском раду "Коника". Захваљујући његовом раду у геометрији, појавиле су се дефиниције кривих: параболе, елипсе, хиперболе. Размислите, и овде је стожац.

Узми прави кружни конус. Ако га раван сијече окомито на ос, тада се у том дијелу формира круг. Када секант пређе конус под углом у односу на осу, добија се елипса у секцији.

Секантна равнина окомита на базу и паралелна са оси конуса формира хиперболу на површини. Равнина која сече конус под углом у односу на базу и паралелна је са тангентом на стожац ствара криву на површини, која се назива парабола.

Решавање проблема

Чак и једноставни задатак како направити канту одређеног волумена захтијева знање. На пример, потребно је да израчунате величину кашике тако да има запремину од 10 литара.

Гивен:

В = 10 л = 10 дм ³ ;

Р1 = 15 цм;

Р2 = 25 цм.

Замах конуса има облик који је схематски приказан на слици 3.

Л - формирање конуса.

Да бисте сазнали површину кашике, која се израчунава по следећој формули:

С = н * (Р ₁ + Р ₂ ) * Л,

потребно је израчунати генератор. Налазимо га из запремине В = н * (Р1 ² + Р ₂ ² + Р ₁ * Р ₂ ) * Х / 3.

Отуда, Х = 3В / н * (Р'2 + Р2 + Р1 * Р2).

Скраћени конус се формира ротирањем правоугаоног трапеза, у коме бочна страна формира конус.

Л2 = ( _Р2Р1 ) ² + Х2.

Сада имамо све податке за израду канта за цртање.

Зашто су ватрене канте обликоване као конус?

Ко је помислио, зашто ватрене канте имају наизглед чудан конични облик? И ово није само. Испоставило се да конусна корпа за гашење пожара има многе предности у односу на конвенционални, скраћени конусни облик.

Прво, како се испоставило, пожарна канта се брже пуни водом и не просипа када се носи. Конус који је већи од обичне кашике допушта више воде за пренос.

Друго, вода из ње се може избацити на већу удаљеност од обичне кашике.

Треће, ако се конусна корпа ослободи руку и падне у ватру, онда се сва вода излије на извор пожара.

Сви ови фактори могу уштедети време - главни фактор у гашењу пожара.

Практична примена

Ученици често имају питање о томе зашто би требали научити како да израчунају волумен различитих геометријских тијела, укључујући конус.

И пројектанти се стално суочавају са потребом да израчунају обим коничних делова механизама. То су врхови бушилица, делови токарских и глодалица. Конусни облик омогућиће бушилицама да лако уђу у материјал, без потребе за почетним ломљењем специјалним алатом.

Запремина стошца има гомилу песка или земље, изливена на земљу. Ако је потребно, једноставним мерењима можете израчунати његов волумен. Неки ће бити збуњени питањем како пронаћи радијус и висину хрпе песка. Наоружани мјерном траком, измјерите опсег брежуљка Ц. По формули Р ​​= Ц / 2н, учимо радијус. Бацајући конопац (мерач траке) преко врха, налазимо дужину генератора. И израчунати висину Питагорине теореме и волумен није тежак. Наравно, таква калкулација је приближна, али вам омогућава да утврдите да ли нисте преварили доносећи тону песка уместо коцке.

Неке зграде имају облик крњег стошца. На примјер, телевизијска кула Останкино се приближава стожастом облику. Може се представити као да се састоје од два конуса постављена један на други. Куполе древних двораца и катедрала су стожац, чији је обим древних архитеката израчунат са задивљујућом прецизношћу.

Ако пажљиво погледате околне објекте, многи од њих су чуњићи:

• лименке за заливање течности;
• хорн лоудспеакер;
• паркинг купе;
• светиљка за лампу за под;
• познато божићно дрвце;
• винд инструментс.

Као што се може видети из горе наведених примера, могућност израчунавања запремине конуса, површина његове површине је неопходна у професионалном и свакодневном животу. Надамо се да ће вам чланак помоћи.