Шта је предикат: дефиниција и примери

Шта је предикат? Ова реч се налази у лингвистици, математици, филозофији и програмирању. Али зар не може бити тако да у овим веома различитим наукама ова реч има исто значење? Математичка логика даје своју посебну интерпретацију овог појма. Почнимо с тим.

Предикат у математици

У математичкој логици, предикат се обично схвата као функција П: Кс → {труе, фалсе}, назван предикат Кс. Међутим, предикати имају много различитих апликација и интерпретација у математици и логици, а њихова тачна дефиниција, значење и употреба варирају од теорије до теорије. Тако, на пример, ако теорија дефинише концепт релације, онда је предикат једноставно карактеристична функција, иначе позната као индикаторска функција релације. Међутим, нису све теорије повезане или засноване на теорији скупова, тако да морате бити пажљиви са исправном дефиницијом и семантичком интерпретацијом предиката.

Тачно или нетачно

Ако још увек не разумете шта је предикат у математици, вреди се детаљније осврнути на то. Неформално, предикат је изјава која може бити истинита или лажна, у зависности од вредности њених варијабли. Може се сматрати оператором или функцијом која враћа вриједност која је истинита или лажна. На пример, предикати се понекад користе за одређивање скупа елемената: када говоримо о скуповима, понекад је неприкладно или немогуће описати скуп навођењем свих његових елемената. Дакле, предикат П (к) ће бити истинит или неистинит, зависно од тога да ли к припада скупу.

Својства објекта

Предикати у математичкој логици су такође широко коришћени да говоре о својствима објеката, дефинишући скуп свих објеката који имају заједничко својство. Тако, на пример, када је П предикат Кс, понекад се може рећи да је П својство Кс. Слично томе, ознака П (к) се користи за означавање реченице или изјаве П у односу на објекат променљиве Кс. к | П (к)} и је скуп објеката за које је П тачно.

На пример, {к | к је позитиван цијели број мањи од 4} је скуп {1,2,3}.

Ако је т елемент скупа {к | П (к)}, онда је тврдња П (т) истинита.

Овде се П (к) назива предикат, а к је резервисано место. Понекад се П (к) назива и пропозициона функција, јер сваки избор са Кс ствара реченицу.

Једноставан облик предиката (П) је боолеан израз, иу овом случају, улази у израз су сами вредности комбиноване коришћењем боолеан операција. Боолеов израз са скупом предикатне истине је сложенији феномен.

Формална дефиниција

• Тачна семантичка интерпретација атомске формуле и атомске реченице ће варирати од теорије до теорије.
• У логици пропозиције, атомске формуле се називају пропозиционе варијабле. У неком смислу, то су предикати са нултим вредностима.
• У логици првог реда, атомска формула се састоји од предикатног симбола примењеног на одговарајући број чланова.
• У теорији скупова, предикати се схватају као карактеристичне функције или дефинишу функције индикатора, односно функције од датог елемента до вредности истине.
• Метода конструисања типова пресуда користи предикате да би их се одредило.
• У ауто-епистемичној логици, која одбацује закон искључених средина, предикати могу бити истинити, лажни или једноставно непознати, то јест, овај скуп чињеница можда није довољан да би се утврдила истина или неистина предиката.
• У фази логици, предикати су карактеристичне функције расподеле вероватноће. То јест, стриктна истинита / лажна процена предиката замењена је вредношћу која се тумачи као степен истине.

Граммар Предицате

Постоје два конкурентна предикатна концепта у граматичким теоријама. Конкуренција између ова два концепта створила је конфузију у погледу употребе термина "предикат" у граматичким теоријама. Дакле, шта је предикат? Овај чланак покрива оба ова појма.

Први концепт се односи на традиционалну граматику, која тежи да разматра предикат као један од два главна дијела реченице, други дио је предмет. Сврха предиката је да употпуни идеју субјекта, на пример, шта ради или шта је.

Други концепт је изведен из рада у предикатском рачуну (логика предиката, логика првог реда) и истакнут је у модерним теоријама синтаксе и граматике. У овом приступу, реченица предиката у основи одговара главном глаголу и свим помоћним средствима која прате главни глагол. Истовремено, његови аргументи (на пример, именице) су изван предиката.

У традиционалној граматици

Појам П у традиционалној граматици инспириран је пропозицијском логиком антике (за разлику од модерније логике предиката). Предикат се сматра својином коју субјект има. Према томе, предикат је израз који може бити истинит. Дакле, израз "потези" важи за све што се креће. Ово даје одговор на питање шта је предикат.

Такво класично разумевање предиката било је више или мање директно у латинском и грчком граматику, а одатле је упало у граматику енглеског и руског језика, где се директно примењује на анализу структуре реченице. Ово разумевање П се такође користи у речницима на енглеском језику.

Предмет и Предикат

Предикат је један од два главна дијела реченице (други је предмет који предикат модифицира). Она мора да садржи глагол, а глагол захтева или дозвољава другим елементима да попуне предикат.

Предикат даје информације о субјекту: шта је то, шта субјект ради, или шта је предмет. Веза између субјекта и његовог предиката се понекад назива језиком предиката. Њена номинална вредност је именска фраза. На примјер, у изразу "Георге ИИИ - краљ Енглеске", краљ Енглеске је предикативни назив. Субјект и предикативна вриједност морају бити повезани повезујућим глаголом, који се назива и копула. Предмет и предикативни придјев такође морају бити повезани заједно.

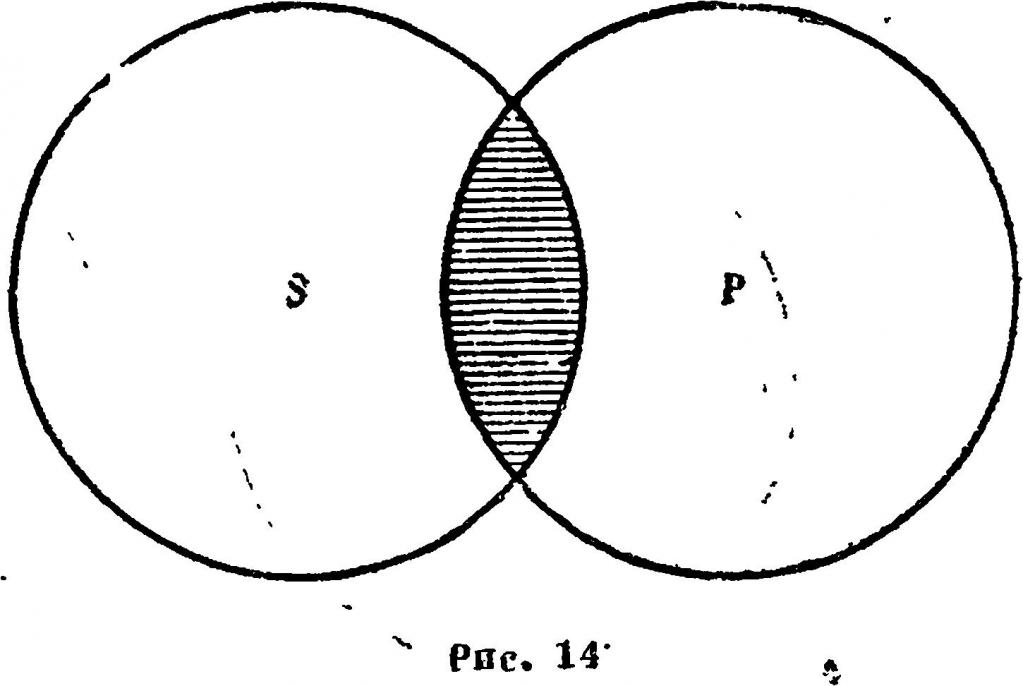
У синтакси

Синтактички П указује на синтактичку валидност употребе дела у формалној граматици и сличан је семантичком предикату који одређује семантичку реалност примене дела. У својој иницијалној имплементацији, синтактички предикати су имали облик “(α)?” И могли би се појавити само на лијевом рубу дјела. Неопходан синтактички услов α може да буде било који важећи фрагмент граматике без контекста.

Формалније, синтактички предикат је облик производног пресека који се користи у спецификацијама парсера или у формалним граматикама. У том смислу израз има значење математичке функције индикатора. Ако су п1 и п2 производна правила, језик који генеришу и п1 и п2 је њихова дата раскрсница.

Рефлективни граматички изрази (ПЕГс), које је измислио Бриан Форд, проширују ове једноставне П, дозвољавајући им да се појаве било где унутар производње заједно са "не-предикатима". Штавише, Форд је изумео процедуру парсирања за обраду ових граматика у линеарном времену.

Овај приступ је имплементиран у АНТЛР верзији 3, која користи детерминистичке државне машине за гледање. Ово може захтевати тестирање предиката за избор између синтактичких прелаза (такозвани “пре-ЛЛ (*)” парсирање).

У модерним теоријама синтаксе

Већина модерних теорија синтаксе и граматике потиче из теорије предикатног рачуна повезане са Готтлоб Фреге. Ово схватање види предикате као односе или функције које стоје изнад аргумената. Користе се или за додељивање својства једном аргументу или за повезивање два или више аргумената. Предлози се састоје од предиката и њихових аргумената (и додатака) и стога су структуре аргумента предиката. У складу са њима, овај П се сматра да повезује своје аргументе са већом структуром.

Предикати се постављају лијево изван заграда, док се њихови аргументи налазе унутар заграда. Једна препознаје валантност предиката, према којој може бити доступна (није приказана), моновалентна, бивалентна или тровалентна. Ови типови репрезентација су слични формалним семантичким анализама, где говоримо о правилном обрачунавању чињеница квантификатора и логичких оператора. Међутим, у односу на основну структуру реченице, ови прикази пре свега претпостављају да су глаголи предикати, а именице које се појављују су њихови аргументи. Са овим разумевањем реченице, бинарна подела реченице на предмет НП и предикат ВП је једва могућа. Умјесто тога, глагол је предикат, а именице су његови аргументи.

Ин логиц

Логика првог реда, позната и као предикат рачунања првог реда и логика предиката, је скуп формалних система који се користе у математици, филозофији, лингвистици и рачунарству. Логика првог реда користи квантизоване променљиве над објектима и дозвољава употребу реченица које садрже променљиве. То га разликује од пропозиционе логике, која не користи квантификаторе или односе.

Логика првог реда

Такве теорије, по правилу, су део логике првог реда, заједно са одређеним подручјем дискурса, у коме се квантификоване варијабле разликују. Понекад се теорија схвата у формалном смислу, а то је само скуп реченица у логици првог реда.

Коришћени придеви разликују логику првог реда од логике вишег реда, у којој постоје, имајући дефинисање предиката или функција као аргументе, или у којима је дозвољен један или оба предикатна квантификатора или квантификатор функције. У теоријама првог реда, предикати су често повезани са скуповима. У интерпретативним теоријама вишег реда оне се могу тумачити као скупови. Нешто слично се користи у дефинисању предиката у програмирању. То не изненађује, јер је математика постала нека врста сировине за ову науку.

Теоријски део

Постоје многи дедуктивни системи за типове пресуда и логику првог реда, који су оба звучни (све доказиве тврдње истините у свим моделима) и потпуне (тврдње које су тачне за све моделе су доказиве). Иако је релација логичке последице само полупропустљива, у аутоматизованој теореми која је доказана у логици првог реда, остварен је значајан напредак. Логика првог реда такође задовољава неколико металогичких теорема које га чине погодним за анализу у теорији доказа, као што су Левенхеим-Сколем-ова теорема и теорема компактности.

Логика првог реда је стандард за формализацију математике у аксиомима и проучава се у основама математике. Пеано аритметика и Зермело-Фраенкелова теорија скупова су аксиоматизације теорије бројева и теорија скупова, односно, дио су логике првог реда. Међутим, теорија првог реда нема способност да јединствено опише структуру са бесконачним регионом, на пример природни бројеви. Аксиомски системи који у потпуности описују ове две структуре (то јест, категоријални аксиомски системи) могу се добити у јачим облицима логике, као што је логика другог реда.

Основе логике првог реда самостално су развили Готтлоб Фреге и Цхарлес Сандерс Пиерце.