Шта је убрзање? Типови убрзања. Формуле. Пример решавања проблема

Одељак физике који је задужен за проучавање карактеристика кретања у простору тела зове се кинематика. У овом чланку разматрамо које се физикалне величине у кинематици користе за описивање кретања објеката, као и за откривање убрзања.

Физичке величине у кинематици

Када се тело креће у простору, важно је да знамо која удаљеност путује унутар одређеног временског периода и дуж које се путање креће.

Да би се описале удаљености путују у физици, користи се појам путање - Л. У случају кретања дуж круга, умјесто путање, користи се појам ротацијског кута θ. Вредност Л у СИ се мери у метрима (м), а вредност θ се мери у радијанима (рад.).

Поред стазе, важно је знати и брзину кретања тела. Под њом се разумије брзина пролаза удаљености. Математички израз за линеарну брзину има облик:

в¯ = д Л / дт

За описивање кретања у кругу примените угаону брзину ω, која се израчунава на следећи начин:

ω¯ = д θ / дт

Трећа важна количина кинематике је убрзање.

Шта је убрзање? Ово је количина у физици, која показује колико брзо брзина варира током времена. Математички, ово се може написати као:

а¯ = д в¯ / дт

Ако заменимо израз за брзину овој формули убрзања, добијамо:

а = д ² Л / дт ²

Убрзање је први дериват брзине током времена или други дериват над временом путовања.

Тангенцијално и нормално убрзање

Изнад је дата дефиниција убрзања. Назива се комплетна. У општем случају, правац пуног убрзања не подудара се са правцем вектора брзине. Ово последње је тангентно на путању кретања на било којој тачки.

Пошто је брзина векторска величина, промена подразумева могућност промене модула и правца. У првом случају, кажу да тело има тангенцијално убрзање, у другом случају је нормално.

Формула за тангенцијално убрзање а _т се не разликује од оне за убрзавање пуне а. Формула има форму:

а _т = дв / дт

То јест, тангенцијално, или тангенцијално, како се још назива, убрзање се изводи из модула брзине током времена. Вектор а _т ¯ подудара се са вектором в ¯ са убрзаним кретањем и супротан је са успореним покретом.

Нормално убрзање је физичка величина која доводи до закривљености правоцртне путање кретања тијела. Она је усмерена дуж радијуса кривине трајекторије, то јест, нормално у односу на њу. Формула за њену дефиницију је:

а _ц = в ² / р

Нормално убрзање а _ц зависи од модула брзине в и радијуса закривљености трајекторије р. Очигледно, у случају кретања дуж правог радијуса, р се може сматрати једнаким бесконачности. Ово последње значи да је нормално убрзање нула за праволинијско кретање.

За кружна кретања, вектор а _ц ¯ је усмерен ка свом центру дуж радијуса. Из тог разлога, вредност _{ц се} назива и центрипетално убрзање.

Фулл аццелератион

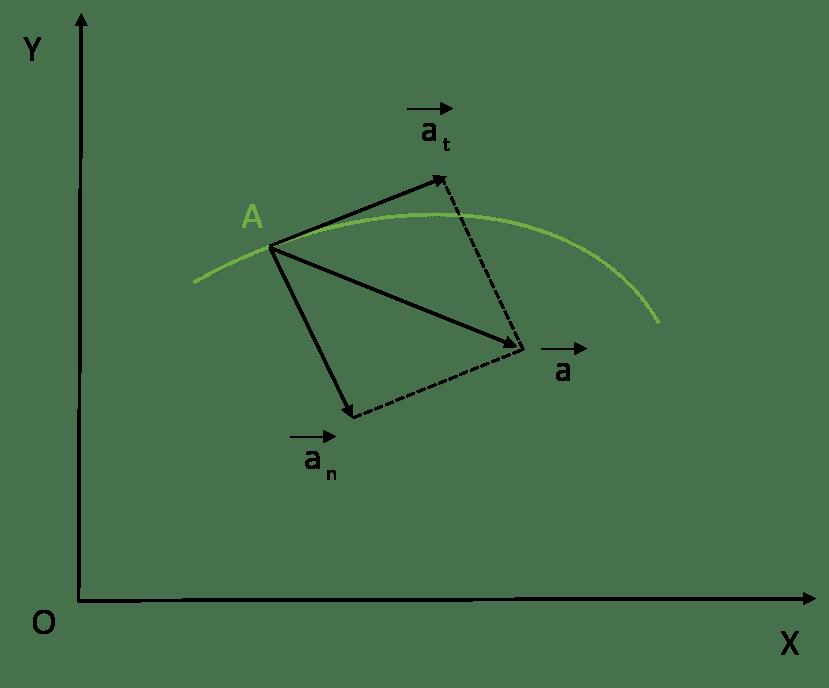
Вектор укупног убрзања је увек сума тангенцијалних и нормалних компоненти. Будући да су међусобно окомити, Питагорина теорема се може користити за израчунавање укупног модула убрзања. Жељена формула за потпуно убрзање поприма облик:

а = √ (а _т ² + а _ц ² )

Да би се одредило где је вектор а¯ усмерен, довољно је израчунати угао између њега и било које компоненте. На пример, угао тхе између вектора а и а _т је једнак:

ар = арцтг (а _ц / а _т )

Подсетимо се да је центрипетално убрзање различито од нуле само када је закривљеност путање различита од бесконачности. У случају праволинијског кретања, укупно убрзање у магнитуди и правцу једнако је тангенцијалној компоненти.

Кутно убрзање

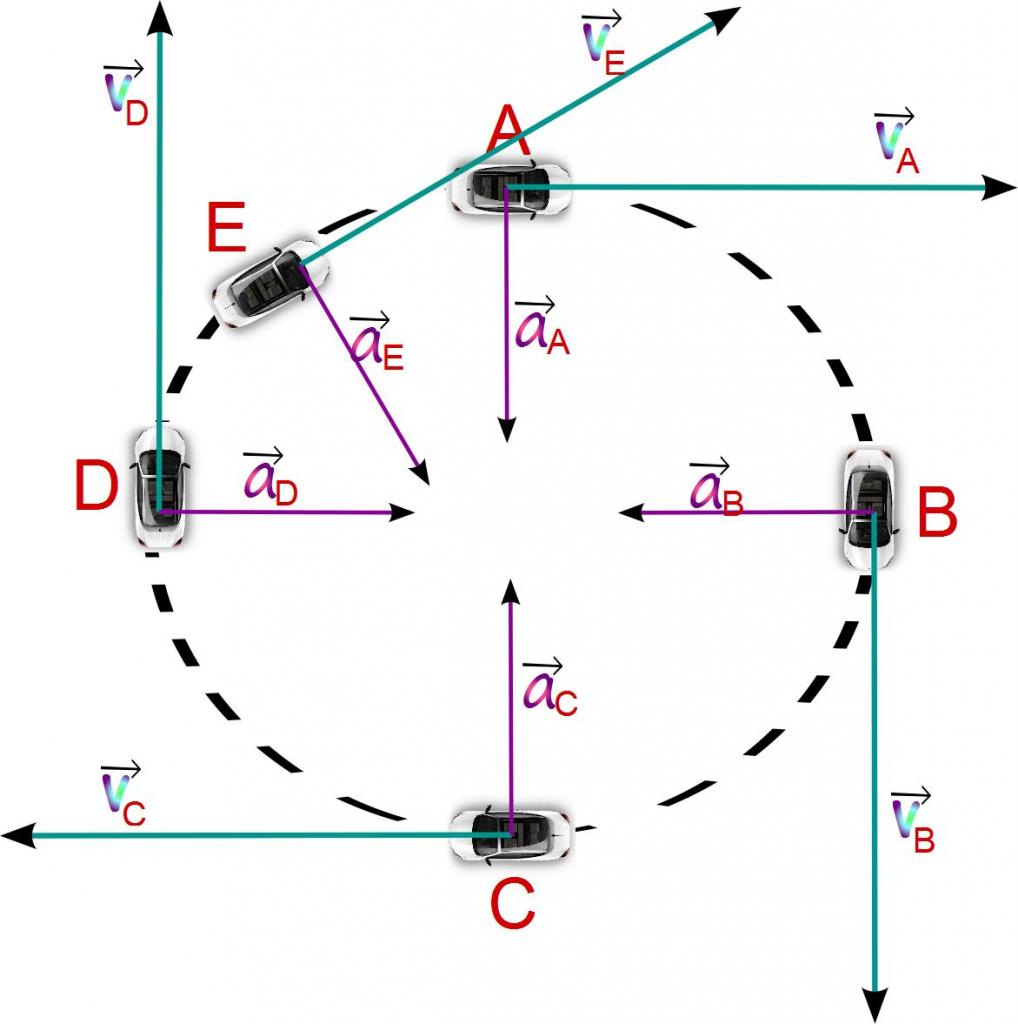
С обзиром на то да је такво убрзање неопходно да се задржимо на одговарајућој угловној карактеристици.

Изнад је уведен концепт угаоне брзине, који се мери у радијанима у секунди (рад / с). Ако нађемо дериват те брзине у односу на време, онда добијемо величину угловног убрзања:

α¯ = ω¯ / дт

Лако је показати да је угаона вредност повезана са тангенцијалном компонентом пуног убрзања следећим односом:

а _т = α × р

Код константног угловног убрзања, тангента компонента а _т ће бити већа за тачке које су удаљеније од осе ротације.

Кутно убрзање нема никакве везе са нормалном компонентом.

Решавање проблема одређивања убрзања

Претпоставимо да се, крећући се са константом убрзања дуж равне линије, тело превалило на удаљености од 100 метара. Познато је да је почетна брзина тела била 1 м / с. Тело је превалило означену удаљеност за 5,5 секунди. Шта је убрзање покрета?

Према стању проблема говоримо о равномерно убрзаном кретању дуж равне путање. Пут који се путује у овом случају може се израчунати по формули:

Л = в ₀ × т + а × т 2/2

Изражавајући из једнакости вредност а, имамо:

а = 2 × (Л - в ₀ × т) / т ²

Све вредности у десној страни једнакости су познате из стања. Замените их и напишите одговор: а = 6,25 м / с ² . То значи да се за сваких 5,5 секунди брзина тела повећава за 6,25 м / с. Пронађена вредност укупног убрзања подудара се са тангенцијалном компонентом.