Шта је то - конус у геометрији. Равни конус са округлом подлогом и његовим карактеристикама

Просторна геометрија, чији се ток одвија у средњој школи, испитује карактеристике и својства различитих геометријских облика у три димензије. Једна од таквих познатих фигура је конус. Да је ово конус, које елементе он описује и која својства поседује, чланак ће одговорити на ова питања.

Конус у геометрији

Са становишта стереометрије, конус је фигура која се формира у простору спајањем правих сегмената одређене тачке са кривом у равни. Ова крива се назива дирецтрик, или водич. Ограничава облик базе. Дирецтрик може бити затворена линија, као што је елипса или круг, или не може бити затворена, као хипербола или парабола. Сви сегменти који повезују дирецтрик са горе поменутом тачком простора називају се генератрици, или генератори. Скуп генератора дефинише конусну површину, а тачка из које излазе назива се врх конуса.

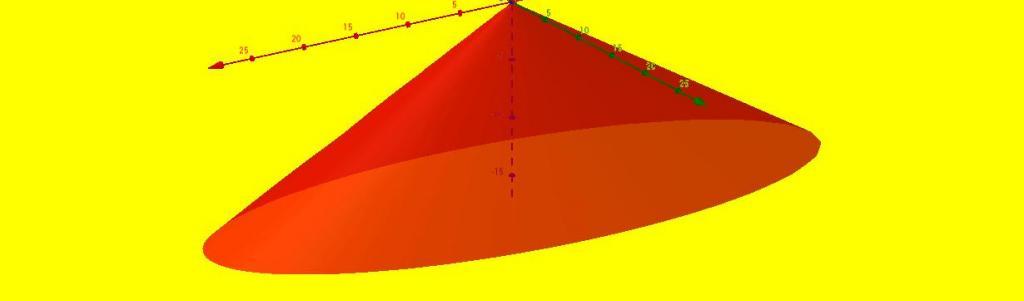
Дакле, конус је фигура која има једну врх, без ивица, и састоји се од две површине (равна основа и бочна стожаста површина). Елиптични конус је приказан на слици изнад.

Кружни или округли конус

Под речју "округли" у наслову ставке разуме се фигура, чија је основа круг. За разлику од других типова конуса, као резултат ротације може се добити округла фигура. Доња слика показује овај процес.

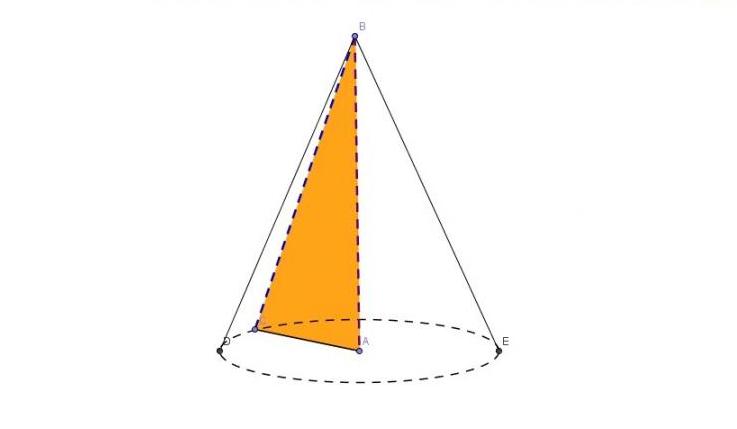
Хајде да укратко објаснимо шта слика показује. Троугао АБЦ је правоугаони. Ако се ротира око ноге АБ, нога АЦ ће описати једну површину конуса, базу и хипотенузу БЦ ће резултирати формирањем коничне површине као резултат ротације.

Конус приказан на слици није само округли, већ и раван. Ово последње својство је важно узети у обзир при извођењу прорачуна линеарних параметара, површине и запремине слике.

Геометријски облик конуса је раван ако висина х пада тачно у центар базе (у овом случају висина је сегмент АБ, а центар базе је тачка А). Ако наведени услов није задовољен, онда се та бројка зове коса. Кутни и равни конуси су приказани испод ради јасноће.

Многи објекти који нас окружују, као што су конуси за сладолед, пругасти стожасти конус или левак за уливање течности кроз уске отворе, имају конусни облик са округлом базом.

Затим ћемо размотрити квантитативне карактеристике равног конуса са округлом базом.

Линеарне димензије и угао у бази

Линеарне димензије конуса су скуп параметара који вам омогућавају да јединствено дефинишете фигуру у простору. Оне су следеће:

• радијус базе р;
• хеигхт х;
• генератрик г.

Треба приметити да су за тип конуса који се разматра све генерације једнаке једна другој и пресецају основу фигуре под истим углом.

Поред горе наведених линеарних параметара, конус је карактерисан и углом тхе између генератора и базе.

Све ове карактеристике су међусобно повезане следећим основним једначинама:

г = √ (х ² + р ² );

г = х / син ();

г = р / цос (φ);

х = р * тг ()

Ове једнакости се могу писати независно ако размотримо правоугаони троугао унутар конуса и присетимо се дефиниција наведених тригонометријских функција.

Површина површине

Подручје базе и конусне површине је важна карактеристика конуса. Јасно је и лакше проучавати површину фигуре не у тродимензионалном, већ у дводимензионалном простору. Да бисте то урадили, направите такозване скениране обрасце. Процес његовог пријема можете замислити на следећи начин: Претпоставимо да постоји конус од папира. Прво сечемо његову базу дуж обима, а затим одрежемо конусну површину дуж генератора и расклопимо је. Добили смо скенирање конуса, који је приказан на слици испод.

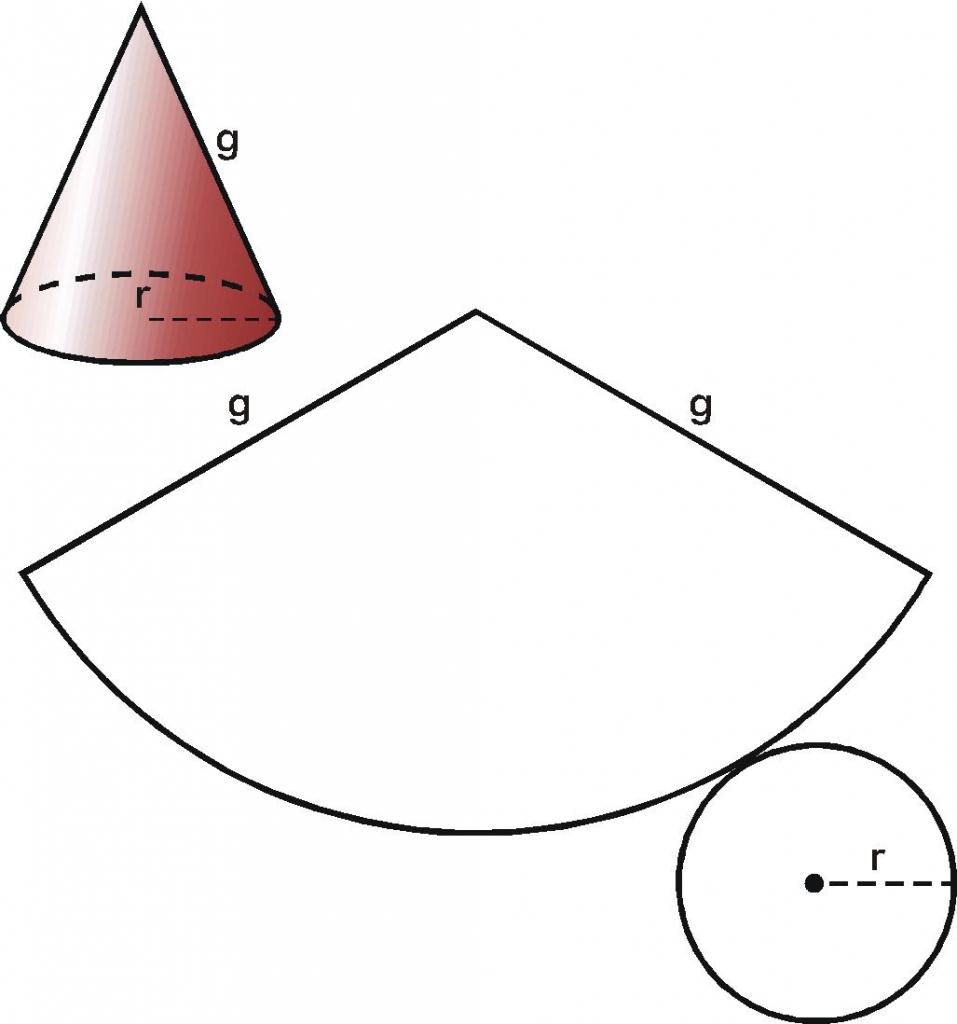
Површина целокупног чишћења С једнака је:

С = С _о + С _б

Када је први термин (С _о ) површина круга, други термин (С _б ) је подручје кружног сектора који одражава конусну површину. Вредност С _о израчунава се по следећој формули:

С _о = пи * р ²

Са кружним сектором ситуација је компликованија. Ограничен је са два радијуса чија је дужина једнака генератрији г, а један лук одговара обиму основног круга. Ове нумеричке информације вам омогућују да јединствено одредите подручје сектора. Нећемо улазити у математичке прорачуне, али ћемо одмах дати коначну формулу за С _б :

С _б = пи * р * г

Поређење писаних формула за С _б и С _о сугерише да је површина бочне површине увек већа од оне за базу помоћу г / р.

Формула за укупну површину је следећа:

С = пи * р * (р + г)

Боди сизе

Стожац је просторна фигура, тако да има одређену запремину. Он нумерички одговара простору простора који је ограничен коничном површином и кружном базом. За одређивање запремине конуса користите следећи израз:

В = 1/3 * С _о * х

Замјењујући у овај израз формулу за С _о , добијамо:

В = 1/3 * пи * р ² * х

Неки читаоци су можда приметили да формула за запремину конуса одговара оној за пирамиду. Ова случајност није случајна, јер облици ових фигура постају идентични ако се број ивица праве пирамиде повећа до бесконачности.