Шта је интегрални? Интеграли са детаљним решењем. Интеграл табле
Реч "интегрални" долази од латинског интегралиса - холистичког. Овај назив је предложен у 17. веку. ученик великог Леибниза (и такође изузетног математичара) И. Бернулија. А шта је интегрални у модерном смислу? У наставку ћемо покушати дати свеобухватан одговор на ово питање.
Историјска позадина концепта интегралног
Почетком 17. века у разматрању водећих научника дошло је до великог броја физичких (прије свега механичких) задатака у којима је било потребно истражити зависности појединих количина од других. Најочитији и најозбиљнији проблеми били су одређивање тренутне брзине неједнаког кретања тела у било ком тренутку и његов обрнути проблем у проналажењу величине путање које је тело спроводило током одређеног временског периода током таквог кретања. Данас већ знамо шта је интеграл брзине кретања - то је пут који је прешао. Али разумевање како да се израчуна, знајући брзину у сваком тренутку у времену, није се појавило одмах.
Прво, из разматрања таквих зависности физичких величина, на пример, путање на брзину, формиран је математички концепт функције и = ф (к). Проучавање својстава различитих функција довело је до појаве математичка анализа. Научници активно траже начине за проучавање својстава различитих функција. 
Како је израчунавање интеграла и деривата?
Након што је Десцартес створио основе аналитичке геометрије и прилику да графички прикаже функционалне зависности у оси картезијанског координатног система, истраживачи су се суочили са два главна задатка: како нацртати тангенту на закривљену линију у било којој тачки и како пронаћи подручје фигуре која је ограничена изнад ове кривуље и праваца, паралелно са координатним осама. На неочекиван начин, испоставило се да је први еквивалент за проналажење тренутне брзине, а други за проналажење пређене удаљености. Уосталом, у случају неједнаког кретања, он је приказан у картезијанским осима координата "удаљеност" и "вријеме" са одређеном закривљеном линијом.
Гениус Леибниз и Невтон средином 17. века. створене су методе које омогућавају рјешавање оба проблема. Показало се да је за провођење тангенте на кривуљу у некој точки потребно пронаћи вриједност тзв. Деривата функције која описује ову кривуљу у њеној точки, а та вриједност је једнака брзини промјене функције, тј. тренутна брзина тела.
Да би се пронашло подручје ограничено кривом, било је потребно израчунати одређени интеграл, који је дао његову тачну вриједност. Деривативни и интегрални - основни појмови диференцијалног и интегралног рачуна, који су основа модерне математичке анализе - најважнији дио више математике.
Површина испод кривине
Дакле, како га дефинисати егзактна вредност? Покушајмо од самог почетка детаљно разрадити процес његовог израчунавања кроз интеграл.
Нека је ф континуирана функција на интервалу [аб]. Размотримо криву и = ф (к) која је приказана на слици испод. Како пронаћи подручје површине ограничено кривуљом), к оси и линије к = а и к = б? То је подручје осјенчане фигуре на слици. 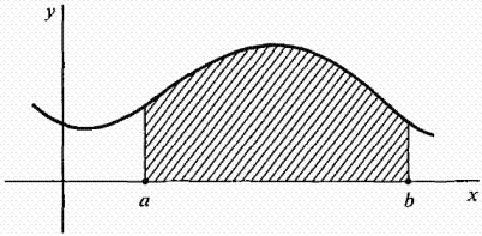
Најједноставнији случај је када је ф константна функција; то јест, крива је хоризонтална линија ф (Кс) = к, где је к константа и к ≥ 0, као што је приказано на слици испод. 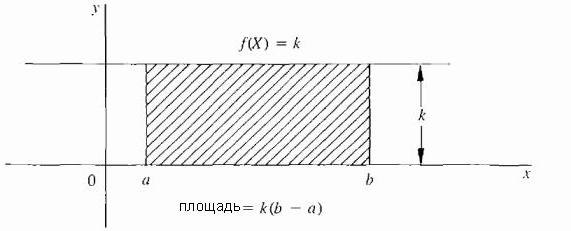 У овом случају, површина испод криве је само правоугаоник са висином к и ширином (б - а), тако да је подручје дефинисано као: к · (б - а).
У овом случају, површина испод криве је само правоугаоник са висином к и ширином (б - а), тако да је подручје дефинисано као: к · (б - а).
Подручја неких других једноставних облика, као што су трокут, трапез и полукруг, дају планиметријске формуле.
Површина под било којом континуираном кривуљом и = ф (к) је одређена одређеним интегралом, који је исписан на исти начин као и регуларни интеграл.
Риеманн сум
Пре него што се упустимо у детаљан одговор на питање шта је интеграл, истакнимо неке основне идеје.
Прво, површина испод криве је подељена на одређени број н вертикалних трака довољно мале ширине Δк. Даље, свака вертикална трака се замењује вертикалним правоугаоником висине ф (к), ширине Δк и површине ф (к) дк. Следећи корак је формирање суме области свих ових правоугаоника, названих Риеманнов сума (види слике испод).
Цртежем наших правоугаоника ,к широко, можемо узети њихову висину једнаку вредности функције на левој ивици сваке траке, тј. Крива ће бити крајње леве тачке њихових горњих кратких страна Δк широке. У исто време, у делу где функција расте, а његова крива је конвексна, сви правоугаоници су испод ове криве, тј. Њихова сума ће сигурно бити мања од тачне вредности површине испод криве у овој области (види слику испод). Овај метод апроксимације назива се леви. 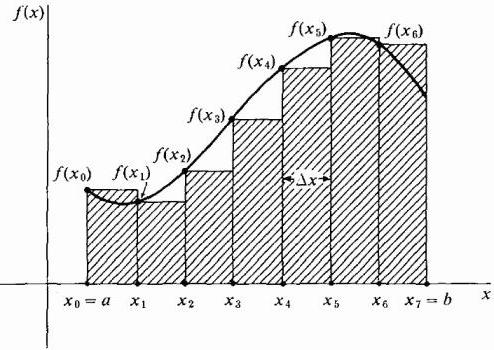
У принципу, могуће је нацртати апроксимационе правоугаоне тако да екстремне десне тачке њихових горњих кратких страна ширине Δк леже на кривој. Тада ће бити веће од кривуље, а апроксимација подручја у овој области ће бити већа од њене тачне вредности, као што је приказано на слици испод. Овај метод се зове право. 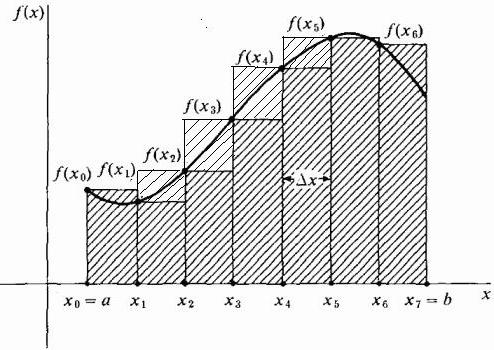
Али такође можемо узети висину сваког од апроксимационих правоугаоника једнаким само некој вредности функције у произвољној тачки к * и унутар одговарајуће траке Δк и (види сл. испод). У овом случају, чак не можемо узети исту ширину свих трака. 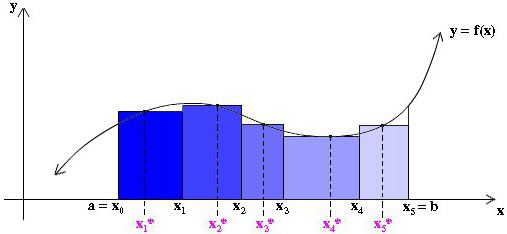
Израђујемо Риеманнов износ:

Прелазак из Риеманнове суме у дефинитивни интеграл
У вишој математици доказана је теорема, која каже да ако је, уз неограничено повећање броја н апроксимираних правоугаоника, њихова највећа ширина тендира нули, онда Риеманнова сума А н тежи ка некој граници А. Број А је исти за било који метод формирања апроксимација правоугаоника и за било који избор тачака к * и .
Јасно објашњење теореме дато је на слици испод.
Показује да, што су ужи правоугаоници, то је ближе подручје степенасте фигуре подручју под кривуљом. Када је број правоугаоника н → ∞, њихова ширина је Δк и → 0, а граница А суме А н је бројчано једнака траженој области. Ово ограничење и постоји одређени интеграл функције ф (к): 
Интегрални симбол, који је модификовани курзив С, увео је Леибниз. Ј. Б. Фоуриер је предложио да се ознака за интеграл стави на њен врх и на дно. Истовремено, јасно су назначене почетне и коначне вриједности к.
Геометријска и механичка интерпретација одређеног интеграла
Покушајмо дати детаљан одговор на питање шта је интегрални? Размотримо интеграл на интервалу [а, б] из позитивне функције ф (к) у њему и претпоставимо да је горња граница већа од доње а Ако су ординате функције ф (к) негативне унутар [а, б], тада је апсолутна вриједност интегралног једнака површини између к-оси и графа и = ф (к), а сам интеграл је негативан. У случају појединачног или поновљеног пресека и = ф (к) оси апсцисе на сегменту [а, б], као што је приказано на слици испод, за израчунавање интеграла, потребно је одредити разлику у којој је смањење једнако укупној површини парцела изнад к-осе и дедуцтибле - укупна површина подручја испод ње. Механичка интерпретација одређеног интеграла је уско повезана са геометријским. Вратимо се на секцију "Риеманнова сума" и замислимо да граф приказан на сликама изражава функцију брзине в = ф (т) са неједнаким кретањем материјална тачка (оса апсцисе је временска оса). Тада ће површина сваког апроксимационог правоугаоника ширине Δт, коју смо изградили током формирања Риеманнове суме, изразити приближно путању тачке за време Δт, односно в (т *) Δт. Укупна сума површина правоугаоника на интервалу од т 1 = а до т 2 = б изражава приближно путању с током времена т 2 - т 1 , и њена граница, тј. интегрални (дефинисани) од а до б функције в = ф (т) преко дт ће дати тачну вредност пута с. Ако се вратимо на његову ознаку, онда можемо добро претпоставити да је а = цонст и б специфична вредност неке независне варијабле к. Тада се одређени интеграл са горњом границом к из конкретног броја претвара у функцију од к. Такав интеграл је једнак површини слике испод кривуље означене тачкама аАБб на слици испод. Претпоставимо да смо дали варијаблу к = б неки мали прираст к. Тада се прираст површине фигуре аАБб састоји од површине правоугаоника (засенченог на слици) Бб Δк и површине БДЦ фигуре испод криве. Површина правоугаоника је једнака Бб к Δк ф = ф (к) Δк, то јест, то је линеарна функција прираста независне варијабле. Површина БДЦ облика је очигледно мања од површине правоугаоника БДЦК = Δк ∙ Δи, а како Δк → 0 има тенденцију, она се смањује чак и брже од ње. Дакле, ф (к) Δк = ф (к) дк је разлика варијабилне површине аАБб, тј. Диференцијала одређеног интеграла Из овога се може закључити да се израчунавање интеграла састоји у проналажењу функција из датих израза њихових диференцијала. Интегрални рачун је управо систем метода за проналажење таквих функција из њихових познатих диференцијала. Она повезује однос између диференцијације и интеграције и показује да постоји операција инверзна према диференцијацији функције - њеној интеграцији. Такође показује да ако је било која функција ф (к) непрекидна, онда применом ове математичке операције на њу можете наћи читав ансамбл (скуп, скуп) функција примитивних за њега (или на други начин пронаћи неодређени интегрални од њега). Нека је функција Ф (к) ознака резултата интеграције функције ф (к). Кореспонденција између ове две функције као резултат интеграције друге од њих је назначена на следећи начин: Као што се може видети, са интегралним симболом нема ограничења за интеграцију. То значи да се из одређеног оно трансформише у неодређени интеграл. Реч "неодређено" значи да резултат операције интеграције у овом случају није једна, већ многе функције. Заиста, осим функције Ф (к), свака функција Ф (к) + Ц задовољава посљедње изразе, гдје је Ц = цонст. То подразумијева да се стални члан у скупштини антидимулатива може произвољно поставити. Треба нагласити да ако је интеграл дефинисан функцијом број, онда је неодређено функција, прецизније, њихов скуп. Термин "интеграција" користи се за дефинисање потраге за оба типа интеграла. То је потпуно супротно од одговарајућег правила за диференцијацију. Како се узимају неограничени интеграли? Примјери ове процедуре разматрамо специфичне функције. Погледајмо моћну функцију општег облика: ф (к) = цк н Након што смо то учинили са сваким изразом у изразу интеграбилне функције (ако их има више), додамо константу на крају. Подсјетимо се да га узимање деривата константне вриједности уништава, тако да узимање интеграла било које функције даје нам обнову ове константе. Означавамо га са Ц, јер је константа непозната - може бити било који број! Према томе, можемо имати бесконачно много израза за неодређени интеграл. Погледајмо једноставне неограничене интеграле, примјери који су приказани испод. Претпоставимо да требате пронаћи интегрални дио функције: ф (к) = 4к 2 + 2к - 3. Почнимо са првим мандатом. Погледамо експоненат 2 и повећамо га за 1, онда поделимо први термин са резултујућим индикатором 3. Добијамо: 4 (к 3 ) / 3. Онда погледамо следећег члана и учинимо исто. Пошто има експонент 1, резултујући индикатор ће бити 2. Дакле, тај члан поделимо са 2: 2 (к 2 ) / 2 = к 2 . Последњи термин има фактор к, али ми га једноставно не видимо. Можемо замислити последњи термин као (-3к 0 ). Ово је еквивалентно (-3) ∙ (1). Ако користимо правило интеграције, додамо 1 индикатору да га подигнемо на први степен, а онда поделимо последњи израз на 1. Добијемо 3к. Ово правило интеграције ради за све вредности н, осим н = - 1 (зато што не можемо делити са 0). Сматрали смо најједноставнији пример проналажења интегралног. Уопштено говорећи, решење интеграла није лак задатак, а већ стечено искуство у математици је добра помоћ у томе. У горњем одељку, видели смо да се из сваке формуле диференцијације добија одговарајућа формула интеграције. Стога су све њихове могуће опције већ дуге и сажете у одговарајућим табелама. Следећа табела интеграла садржи формуле за интеграцију основних алгебарских функција. Ове формуле треба запамтити, памтити их постепено, јер су фиксне вежбе. Друга табела интеграла садржи главне тригонометријске функције: Испоставља се да је за то могуће једноставно интегрирати, тј. Пронаћи неограничене интеграле. И формула оснивача Невтон-Леибнизовог интегро-диференцијалног рачуна помаже у томе. Према томе, у првој фази, израчунавање жељеног интеграла састоји се у проналажењу неодређеног, затим израчунавању вредности пронађеног примитивног Ф (к) са супституцијом од к, која је једнака прво горњој граници, затим до ниже, и коначно, да се утврди разлика ових вредности. У овом случају, константа Ц се не може записати. јер нестаје када се изводи одузимање. Неке интеграле разматрамо са детаљним решењем. Нађите област локације под једним таласом синусног таласа. Ми сада разматрамо интеграле са детаљним решењем које користи својство адитивности у првом примеру, и замену променљиве интермедијарне интеграције у другом примеру. Израчунавамо одређени интегрални део фракционално рационалне функције: и = (1 + т) / т 3 од т = 1 до т = 2. Сада ћемо показати како поједноставити узимање интеграла увођењем интермедијерне варијабле. Претпоставимо да је потребно израчунати интеграл од (к + 1) 2 . Говорили смо о одређеном интегралу за коначни интервал [а, б] функције ф (к) континуираног на њој. Међутим, одређени број специфичних проблема доводи до потребе да се концепт интеграла прошири на случај када су границе (једна или обе) једнаке бесконачности, или када је дисконтинуирана функција. На пример, када се рачунају површине испод кривих, асимптотски се приближавају оси координата. Да би се концепт интеграла проширио на овај случај, поред проласка до границе, приликом израчунавања Риеманнове сума апроксимираних правоугаоника, изводи се још један. Са таквим двоструким пролазом до границе, добија се неисправан интеграл. Насупрот томе, сви горе наведени интеграли се називају исправним. 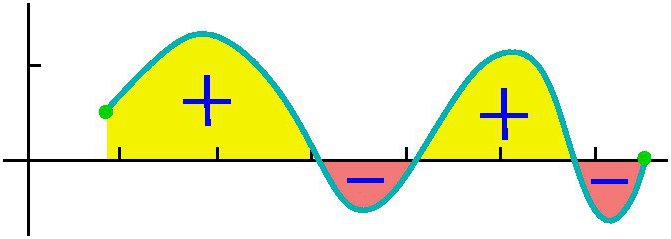 Дакле, за функцију приказану на слици изнад, дефинитивни интеграл од а до б ће бити (С1 + С3) - (С2 + С4).
Дакле, за функцију приказану на слици изнад, дефинитивни интеграл од а до б ће бити (С1 + С3) - (С2 + С4). Диференцијал одређеног интеграла
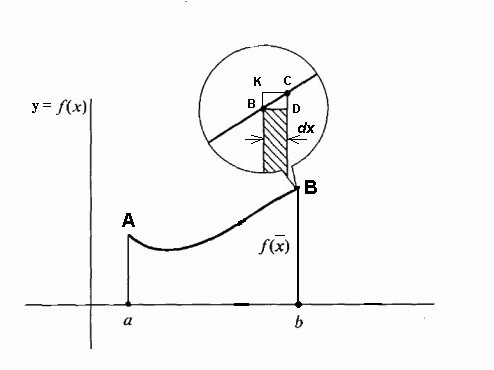 Са фиксном линијом аА и покретним Бб, ова област постаје функција ф (к), при чему су инкременти Δк и даље депоновани дуж к оси, а инкременти функције ф (к) су инкременти површине испод криве.
Са фиксном линијом аА и покретним Бб, ова област постаје функција ф (к), при чему су инкременти Δк и даље депоновани дуж к оси, а инкременти функције ф (к) су инкременти површине испод криве. 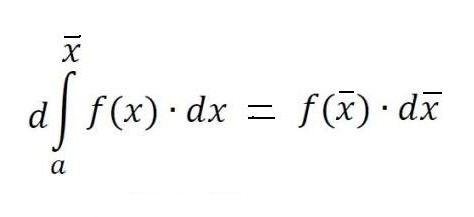
Основни однос интегралног рачуна
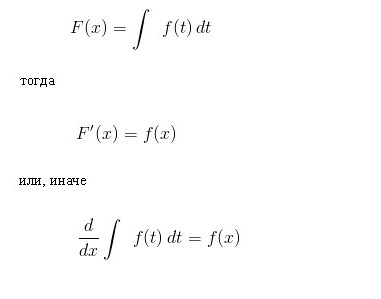
Основно правило интеграције

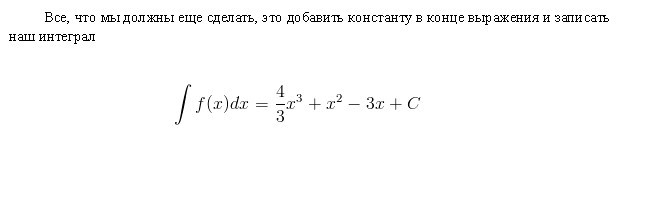

Интегралне табеле
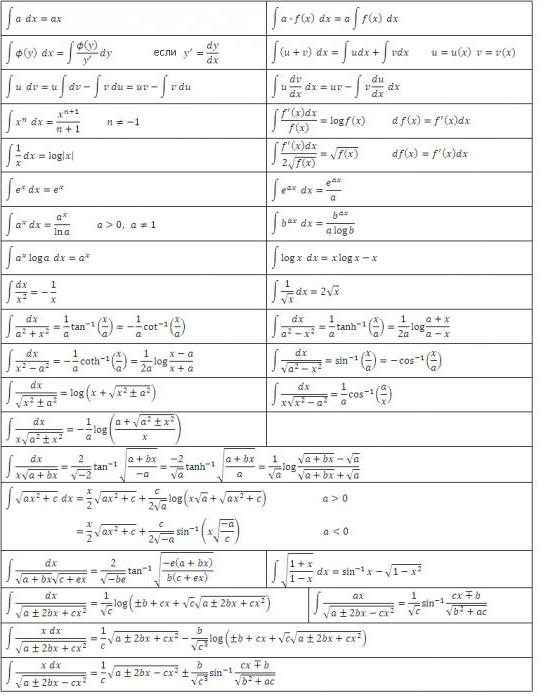

Како израчунати одређени интеграл
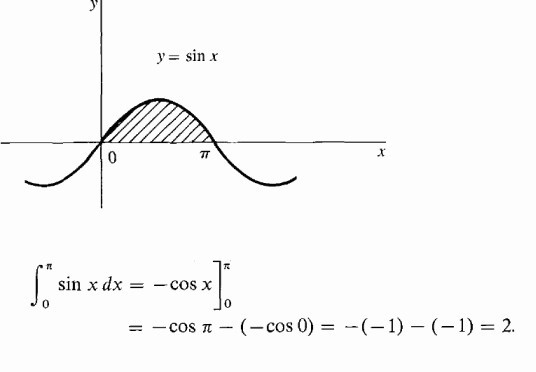 Израчунајте засјењену површину испод хипербола.
Израчунајте засјењену површину испод хипербола. 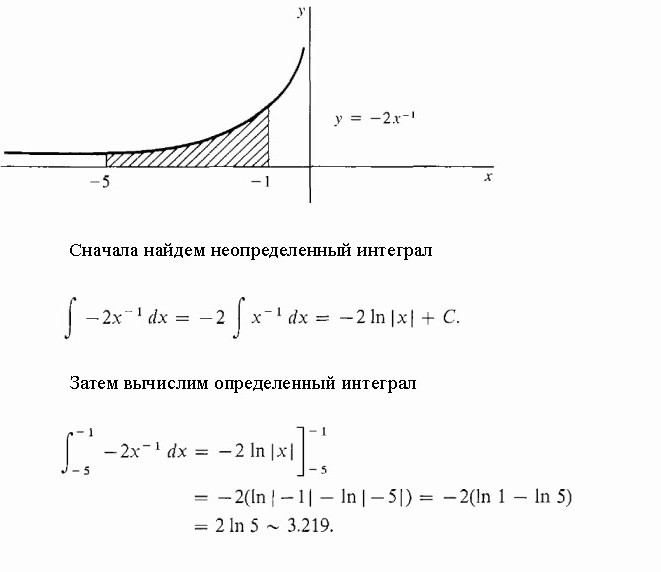
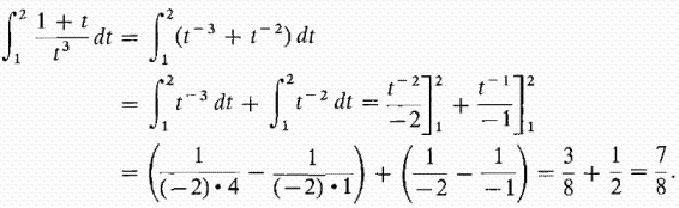
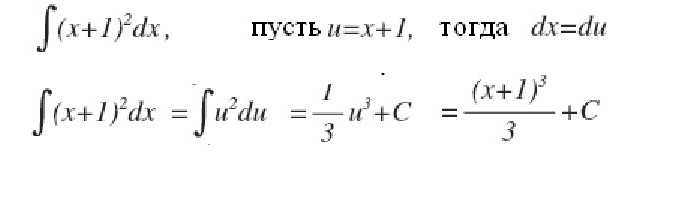
О непрописним интегралима