Који је принцип фарме?
КСВИИ век обележен је брзим развојем у Европи посебног дела физике - оптике. Закони рефлексије и рефракције били су отворени за светлост, а Ферматов принцип је показао зашто они имају одговарајућу математичку форму. Да видимо детаљније шта је то принцип.
Појаве рефракције и рефлексије

Размишљајући, они схватају феномен у коме се светлост, која се шири у њену супстанцу, наилази на препреку на свом путу и драстично мења своју путању. Било која препрека може бити било која: текућа или чврста, прозирна и непрозирна.
Феномен рефлексије познат је још од античких времена. Према историјским доказима, закони рефлексије су већ били формулисани прије наше ере. И у првом веку наше ере, египатски филозоф Херон из Александрије изразио је идеју путање светлости коју је француски Пиерре Фермат касније користио у формулисању свог принципа.

Феномен преламања је лом равне линије уз коју се креће светлост, када прелази преко површине која раздваја два прозирна материјала. Имајте на уму да се у случају рефлексије, сноп креће у једном прозирном материјалу или, како кажу, у једном медију.
Прва формулација закона рефракције се приписује перзијским математичарима из 10. века, одређеном Ибну Сахлу, који се у својим радовима ослањао на дела Клаудија Птоломеја (1.-2. Век не). На крају КСВИ - почетка КСВИИ века, холандски научник Снелл, сумирајући резултате многих експеримената са светлошћу, формулисао је у математичком облику други закон рефракције, који сада носи његово презиме. Снелл је дао своју формулацију у смислу удаљености, а не углова, као што је сада уобичајено. Модерни изглед закона преламања дао је већ Ренеу Десцартесу.
Закони ширења светлости у транспарентним медијима
Пре него што пређемо на разматрање Ферматовог принципа, треба формулисати законе рефракције и рефлексије светлости. За сваку од ових појава, уобичајено је издвојити два закона. Испод су комбиновани у паровима:
- Трајекторија снопа, када прелази границу између два медија, увек лежи у истој равни као и нормала на равни ове границе. Могућа путања зрака се формира у опћем случају из три дијела: упадни сноп, преламање и рефлектирање.
- Ако се угао између снопа упадне светлости и нормале назива θ 1 , исти угао, али за рефлектовани сноп, уписује се као θ 2 , а преломљени угао θ 3 , тада ће други закон изгледати као:
- за рефлексију: θ 1 = θ 2 ;
- за лом: н 1 * син (θ 1 ) = н 2 * син (θ 3 ).
У овим формулама, н 1 и н 2 су индекси преламања у транспарентним медијима 1 и 2. Индекс рефракције, по дефиницији, израчунава се на следећи начин:
н = ц / в.
Овде в и ц су брзине кретања светлосног снопа у медијуму иу вакууму.
Формулација принципа фарме

Пиерре Фермат је био један од познатих математичара и правника Француске у првој половини седамнаестог века. Принцип који носи његово име, он је формулисао 1662, то јест, пола века након што је Снелл открио свој закон за рефракцију.
Укратко, Ферматов принцип се може формулисати на следећи начин: светло, када се креће у апсолутно било којем прозирном медију, бира такву путању, коју пролази у најкраћем времену.
У ствари, ова формулација се не разликује од оне коју је Херон из Александрије учинио једну и по хиљаду година раније за феномен рефлексије. Ипак, Француз га је учинио заједничким за све појаве повезане са светлошћу и показао како се закони лома и рефлексије могу извести из овог принципа.
Закључак првог закона о рефлексији
Користећи Ферматов принцип, закони рефлексије ће се добити математички. Да бисте то урадили, размотрите доњу слику.
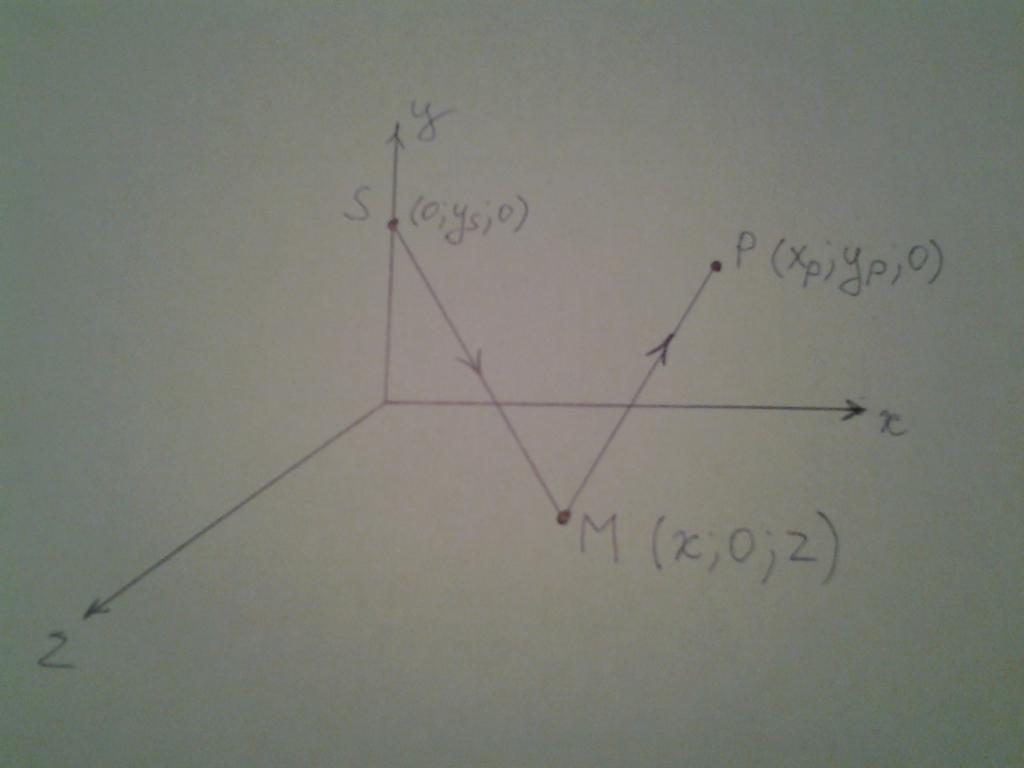
Овде је показано да сноп излази из тачке С, која лежи на и оси. Затим се рефлектује од кз равнине у некој непознатој тачки М. Након рефлексије, сноп се сели у тачку П која лежи на ки равни. Изабрана позиција тачака С и П не утиче на уопштеност даљњег расуђивања, већ само поједностављује математичке прорачуне.
Дакле, записујемо координате сваке тачке:
С (0; иС; 0);
М (к; 0; з);
П (к П ; и П ; 0).
Позиционе координате тачака С и П су познате. Задатак је да се пронађе таква тачка М, која ће одговарати правој путањи СМП која пролази светлосним снопом. Такође претпостављамо да је простор који се разматра хомоген, односно да је брзина светлости у било којој тачки константна вредност.
Према Ферматовом принципу, СМП путања светлости ће проћи у најкраћем времену ако је то најкраће могуће. Пишемо његову дужину:
СМ = √ (к 2 + и С 2 + з 2 ); МП = √ ((кк П ) 2 + и П 2 + з 2 );
СМП = √ (к 2 + и С 2 + з 2 ) + √ ((кк П ) 2 + и П 2 + з 2 ).
Да би се израчунала минимална дужина СМП, потребно је пронаћи парцијалне деривате у односу на к и з (непознате координате тачке М) и изједначити добијене резултате на нулу.
Прво налазимо парцијални дериват у односу на з. Имамо:
СМ (СМП) / =з = з / √ (к 2 + и С 2 + з 2 ) + з / √ ((кк П ) 2 + и П 2 + з 2 ) = 0.
Ова једнакост има један коријен када је з = 0. Другим речима, тачка М лежи на к оси, односно у истој равни као и тачке П и С (раван ки). Из чега следи да ће обновљена норма на равни кз, у којој је, условом проблема, тачка М лоцирана, лежати са СМ и МП у истој равни (ки). Ово је први закон рефлексије.
Закључак другог закона о рефлексији
Наставите да израчунавате претходну ставку. Као што је речено, сада је потребно пронаћи парцијални дериват у односу на к. Имамо:
СМ (СМП) / =к = к / √ (к 2 + и С 2 + з 2 ) + (кк П ) / √ ((кк П ) 2 + и П 2 + з 2 ) = 0.
Задњу једнакост пишемо у облику:
к / СМ + (кк П ) / МП = 0 =>
к / СМ = (к П -к) / МП.
Односи добијени у сваком делу једнакости су синуси углова са врхом у тачкама С и П. Ако сада вратимо нормалу на кз равни кроз тачку М, онда ће означени углови одговарати угловима упадања (између СМ и нормале) и рефлексијама (између МП и нормале). .
Дакле, слиједећи Ферматов принцип, добили смо и други закон рефлексије свјетлости.
Закључак закона преламања Снелл-а
Покажимо сада како се закон рефракције свјетлости може извести из Ферматовог принципа. Да бисте то урадили, размотрите слику сличну претходној.
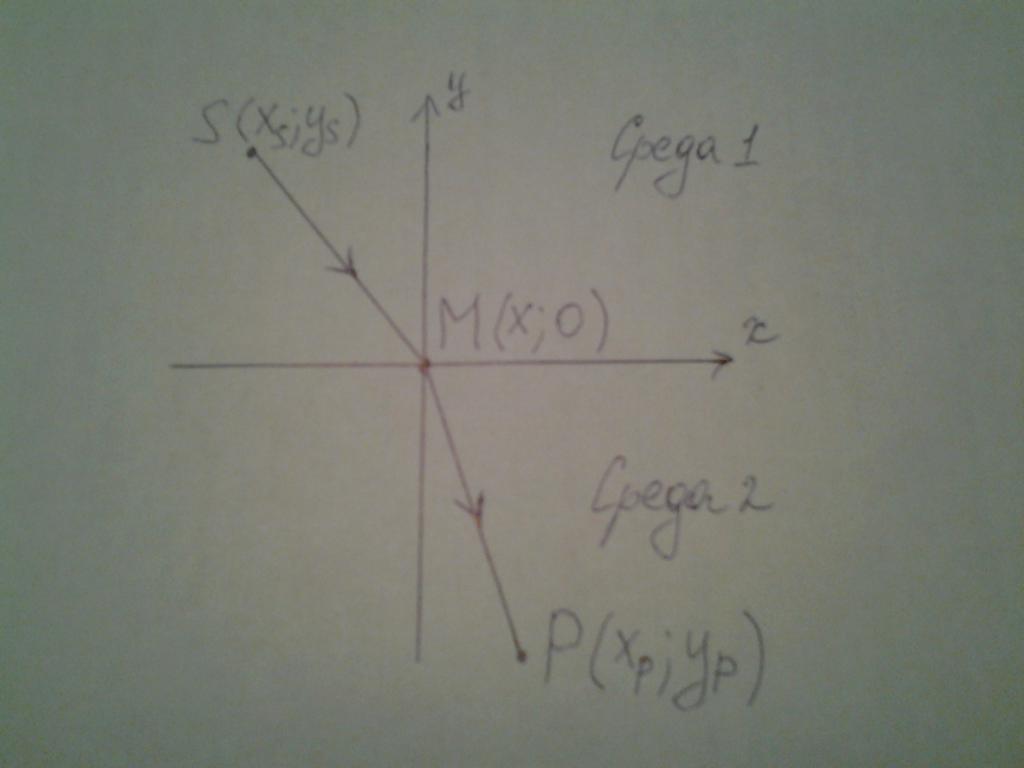
Ради једноставности, размотрићемо случај у ки равни. Записујемо координате извора С и пријемника П светлости, које се налазе у различитим окружењима:
С (к С ; и С );
М (к; 0);
П (к П ; и П ).
Нађимо непознату координату тачке М. Координата и = 0 је за њу тачно позната, јер се управо на граници медија (к оса) мења брзина светлости. Дужине сегмената СМ и МП су једнаке:
СМ = √ (кк С ) 2 + и С 2 );
МП = к (к П -к) 2 + и П 2 ).
Укупно време које светло троши на СМП путању биће једнако:
т = СМ / в 1 + МП / в2.
Овде су в 1 и в 2 брзине протока у одговарајућем медију. Да бисмо пронашли минимално време кретања, треба узети укупни дериват у односу на променљиву к и изједначити га са нулом. Добијамо:
дт / дк = (кк С ) / (√ (кк С ) 2 + и С 2 ) * в 1 ) - (к П -к) / (√ (к П -к) 2 + и П 2 ) * в 2 ) = 0 =>
(кк С ) / (СМ * в 1 ) = (к П -к) / (МП * в 2 ).
Користећи функције синуса угла упада θ 1 и рефракције θ 3 , добијамо:
син (θ 1 ) / в 1 = син (θ 3 ) / в 2 .
Да би се стечена једнакост довела до Снелловог закона у прикладном облику (преко индекса преламања медија), потребно је помножити леву и десну страну брзином светлости ц.

Према томе, примена Ферматовог принципа олакшава закључивање закона за главне појаве кретања светлосног снопа у транспарентним материјалима.
Кретање светлости у нехомогеној средини
Случајеви који су горе разматрани претпостављају да је материјал хомоген и да светлосни сноп задржава своју брзину када се креће. У случају нехомогених медија важи следећа једнакост:
Л = (н (к, и, з) * дл.
Овај интеграл се узима дуж путање свјетлости. Диференцијално дл је сегмент путање за који медиј задржава своју хомогеност. Вредност н (к, и, з) је локални индекс рефракције.
Поменути интеграл се обично назива интегрални оптички пут. Принцип фарме за оптички пут укључује проналажење екстрема за Л.
Општа формулација принципа који се разматра
Принцип минималног времена за кретање светлости је посебан у општој формулацији. Тренутно, Ферматов генерализовани принцип је формулисан на следећи начин: светло бира путању током кретања која одговара екстремима оптичке путање.
Екстреми функције, према математичкој дефиницији, су минимална, максимална и инфлексијска точка. Општи принцип Фермата задовољава све ове вредности, тј. Путања светлости не мора нужно бити минимална, може бити и максимална и одговарајућа тачка инфлексије оптичке путање.
Домаћа аналогија са разматраним принципом
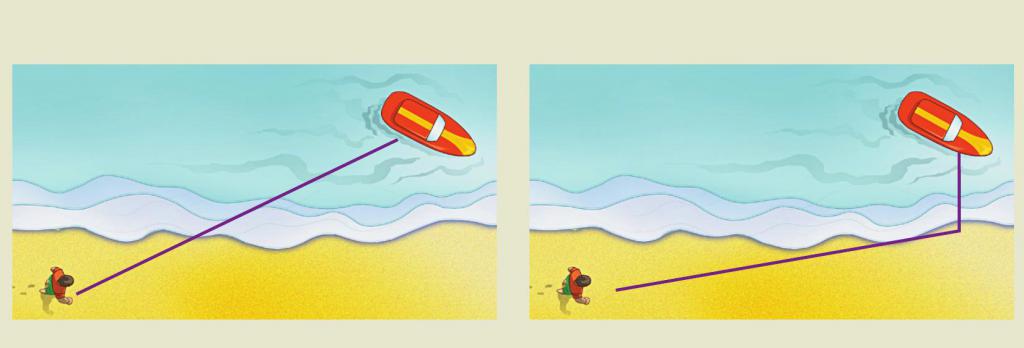
Општи принцип Фермата је пак посебан случај тзв. Принципа најмање акције. Овде нећемо дати одговарајуће дефиниције и њихове математичке формулације, међутим, покажимо где се може применити принцип који су предложили Французи.
Користи се у решавању једноставног, на први поглед, свакодневног задатка: на пример, особа се утапа у мору близу плаже. Како да се спасилац креће на обалу да би спасио утопљеника? Наравно, требало би да дође на спашавање у најмањој количини времена. Будући да је брзина кретања спасиоца на плажи већа него на води, он би требао проћи неку удаљеност дуж обале, а тек онда скочити у воду и пливати. То јест, задатак је сведен на примену принципа Фермата, где улогу светлосног снопа игра спасилац.
Приметимо да решење овог проблема није једноставно, јер се у његовом процесу појављују једначине 4. степена.
Према томе, Ферматов принцип је средство за добијање основних закона пропагације светлости. Међутим, то није фундаментално. Може се рећи да следи из Хуигенсовог принципа о изворима секундарних сферних таласа.