Алгебарска прогресија: формуле и примери решења
Овај чланак ће говорити о алгебарској прогресији, формулама неопходним за рјешавање проблема са њеним учешћем, као и неке примјере њихове употребе. Ради комплетности, укратко ћемо говорити о другој врсти прогресије - геометријској.
Појам алгебарске прогресије

Свака серија бројева која је уређена према неком закону може се назвати прогресијом. Најпопуларније и најчешће коришћене за решавање практичних проблема су две врсте таквих серија: алгебарска и геометријска прогресија. Размотримо први од њих детаљније.
Алгебраика се често назива аритметичка прогресија. Математички, то значи следеће:
а н = а н-1 + д
Дакле, говоримо о таквој нумеричкој секвенци у којој се било који од њених чланова разликује од претходног или следећег истим бројем д. Овај број се назива разлика (може се одредити проналажењем разлике између два сусједна елемента прогресије).
Према овој дефиницији, напредак који се разматра има почетак, али нема краја. Увек почиње са термином а 1 (било који реални број), а затим наставља са сабирањем овог члана са разликом д. Сходно томе, може бити бесконачно повећана (д> 0) или опада (д <0). Ситуација када је д = 0 такође се може сматрати посебним случајем аритметичке прогресије представљене бесконачном секвенцом идентичних бројева.
Формула за проналажење произвољног члана
Као што је горе објашњено, разматрани тип прогресије је јединствено одређен његовим првим елементом и разликом, међутим ово правило се односи на све друге вредности. На пример, познавање два произвољна елемента или једног елемента и сума одређеног броја чланова такође јединствено одређује прогресију.
Да бисте израчунали н-ти елемент, можете успешно користити следећу формулу:
а н = а 1 + (н - 1) * д
Очигледност ваљаности овог израза је несумњива, и свако је може верификовати замјеном малих вриједности н.
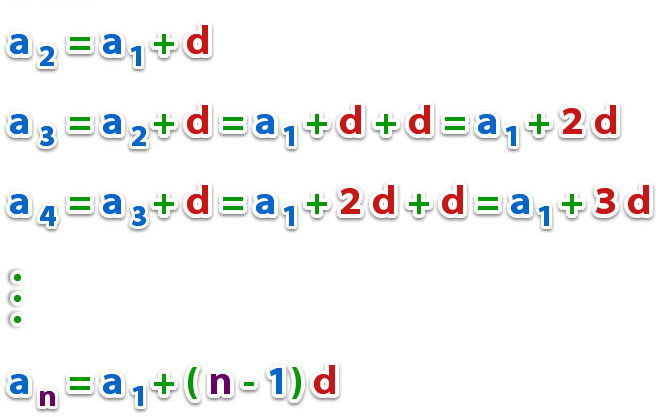
Формула за враћање напредовања два позната елемента
У школском току алгебре, такви проблеми су типични за прогресију: постоје два елемента а н и м , а н> м, потребно је изградити целокупну прогресију на њима.
Овај проблем се решава помоћу формуле за н-тог члана. Напишемо два одговарајућа израза:
а н = а 1 + (н - 1) * д;
а м = а 1 + (м - 1) * д
Пронађите разлику између првог и другог (знак једнакости је сачуван):
а н - а м = (н - м) * д =>
д = (а н - а м ) / (н - м)
Видимо како је лако пронаћи разлику прогресије, ако су два њена члана позната: да би то учинили, одузмите мањи од већег у реду, а затим подијелите резултирајућу разлику за разлику од њихових редних бројева.
Када се пронађе разлика, лако је израчунати први појам (да бисте то урадили, користите било који од прва два израза).
Збир алгебарске прогресије
Друга серија типичних задатака за прогресију је проналажење суме њихових чланова. Следи одговарајућа формула алгебарске прогресије:
С н = ∑ и = 1 н (а и ) = н * (а 1 + а н ) / 2
Односно, да би се одредила сума првих термина од н, треба израчунати збир само два од њих (први и н), помножити са бројем чланова н и поделити резултат на пола.
Изоставили смо математички доказ овог израза, али још увијек пружамо логичан доказ. Може се приметити да, с обзиром на својство разматраног типа прогресије, следећа једнакост увек има:
а 1 + а н = а 2 + а н-1
Заиста, други термин је већи од првог термина за д, али истим претпоследњим (а н-1 ) је мањи од последњег ( н ). У случају пара елемената, добијамо тачно половину таквих сума из укупног броја елемената (н / 2), одакле следи редуцирана формула за С н .

Сматра се да је истакнуту карактеристику аритметичке прогресије први пут установио Карл Гаус, познати математичар с краја 18. - прве половине 19. века, када је у свом уму неколико секунди израчунао збир природних бројева од један до 100.
Примери решавања проблема
Размотримо два примера алгебарске прогресије.
1. Познато је да је девети мандат 7, а 21. је 51. Потребно је пронаћи првих 5 чланова ове аритметичке прогресије.
Услов проблема дозвољава нам да одмах израчунамо разлику д, примењујући формулу са н и а м , која је записана горе. Имамо:
д = (а н - а м ) / (н - м) = (51 - 7) / (21 - 9) = 3,667
По пријему разлике д, извршили смо заокруживање на 3 децимална мјеста.
Сада можете израчунати први елемент серије. Да бисте то урадили, користите податке за 9 чланова:
а 9 = а 1 + д * 8 => а 1 = а 9 - д * 8 = 7 - 3,667 * 8 = -22,336
Да би се решио проблем, остаје да се уради последњи корак: додаје се сукцесивно 4 пута вредност д на први елемент. Добијамо:
а 1 = -22.336;
а 2 = -22,336 + 3,667 = -18,669;
а 3 = -18.669 + 3.677 = -15.002;
а 4 = -15,002 + 3,667 = -11,335;
а 5 = -11,335 + 3,667 = -7,668
Сјетите се да су све израчунате вриједности важеће до трећег децималног мјеста.
2. Радници су пресавијали пилане у облику пирамиде. Познато је да су положили само 33 трупца, а до краја пирамиде недостајала су само три трупца. Потребно је одредити колико редова трупаца су положили радници.
Одговор на ово питање је да се реши алгебарска прогресија, али да би наставили са тим, морате пажљиво да се позабавите овим стањем.
Прво, пошто се трупци сабиру у пирамиду, то значи да је у сваком претходном реду био још један лог, д. 1. Друго, ако је познато да су само три трупца недостајале пре него што је пирамида завршена, онда су остала два горња реда. празно:
а 1 = 1, а 2 = а 1 + д = 2, а 1 + а 2 = 3
Узмемо у обзир ова три дневника, додајући их већ 33 пресавијеним, и одредимо непознати број редова користећи формуле за сум и н-ти члан:
С н = н * (а 1 + а н ) / 2; а н = а 1 + д * (н - 1) =>
С н = н * (а 1 + а 1 + д * (н - 1)) / 2 = (2 * а 1 - д) / 2 * н + д * н 2/2
Познате податке замењујемо последњом једнакошћу и решавамо добијену квадратну једначину за н:
36 = 0.5 * н + 0.5 * н 2 или
н 2 + н - 72 = 0
Дискриминантни: Д = 1 - 4 * 1 * (-72) = 289
Корени: н = (-1 ± 17) / 2 = (8; -9)
Негативну вриједност одмах ћемо одбацити, јер је у супротности са стањем проблема. Дакле, 8 редова пирамиде ће садржати 36 логова. Пошто радници нису довршили два горња реда, то значи да су додали само 6 редова трупаца.
Неколико речи о прогресији геометријског
Алгебраика и геометријска прогресија, по правилу, разматрају се у оквиру једне теме, па је корисно дати идеју о другом типу уређених серија бројева. Дакле, геометријска прогресија је низ бројева који поштују закон:
а н = а н-1 * р
То је, за разлику од аритметике, овде да би добили све елементе, не смете да додате један број, већ да га помножите (р се назива именилац).
Из дефиниције је јасно да геометријска прогресија расте (опада) много брже од аритметичке.
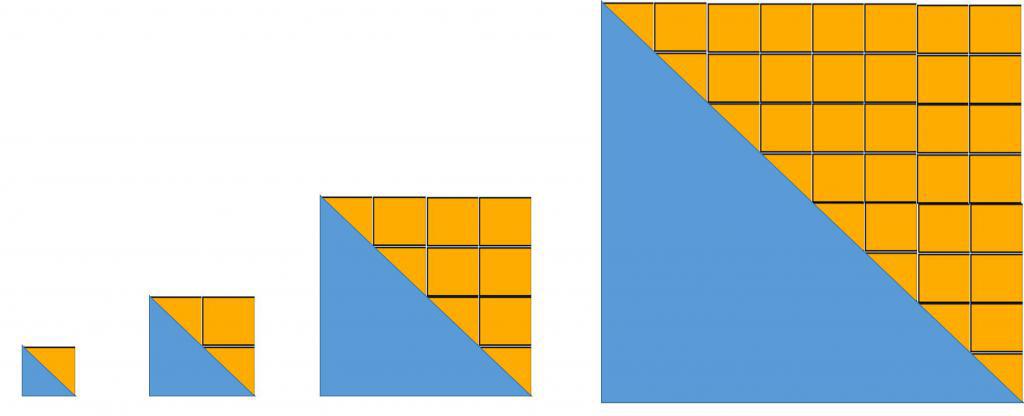
Често се користи у геометрији, на пример, при израчунавању површина фигура користећи њихову поделу на одвојене елементе (метод дељења на пола).