Амперов закон: формулација и примјена

Амперов закон, чија је формулација позната сваком физичару, једна је од четири Маквеллове једначине, које заједно чине основу читаве теорије класичне електродинамике.

Маквеллове једначине

Дио амперовог закона о томе како се електричне струје, извори магнетних поља односе на саму област. Другим речима, ово (заједно са Гаусовим законом за магнетизам) тачно описује слику у којој електричне струје генеришу магнетна поља. Корективни дио Маквелла је значајан јер каже да се магнетна поља појављују када се електрична поља мијењају с временом. Ово је такође важно јер се Маквеллове једначине не слажу без њега. Са корекцијом термина могу се извести формуле спасити електрични набој и предвиђају постојање електромагнетних таласа који путују брзином.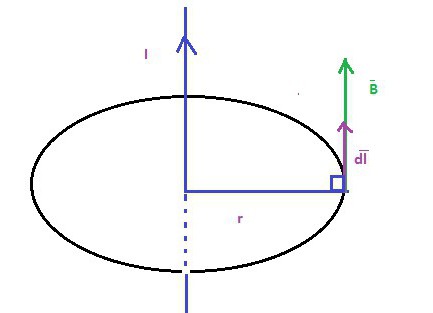

У разумљивом облику, Амперов закон учествује, респективно, у линеарности Маквеллових једначина и, према томе, у целој теорији класичне електродинамике. Ако узмете два струјна разводника и комбинујте их, онда ће магнетно поље бити сума магнетних поља које ствара свака конфигурација.

Маквелл контролни елемент је такође линеаран и стога електромагнетни таласи такође су линеарне. Они се међусобно ометају по принципу суперпозиције и пролазе једни другима без расипања.

Како објаснити закон Ампера једноставним језиком?

Најједноставније објашњење је да жица носи струју. Ако игноришете Магнетно поље Земље може се замислити да вертикална жица са електричном струјом иде горе.

Људи имају тенденцију да говоре о електромагнетизму, али је електрична енергија одвојена од магнетизма, јер је утврђено да електрична енергија и магнетизам утичу једни на друге и могу се комбиновати у систем једнаџби. Посебно у случају проводника под напоном електрична струја производи магнетно поље. Оријентација ових поља није сасвим јасна, али је уочљива. Магнетски компаси могу бити постављени око жица које носе струју, а правци поља се могу видети у правцу тачака игле.

То је могуће узети у обзир због једноставне симетрије. Струја у жици производи магнетно поље, али шта би требало да се догоди са обрасцем у овим пољима ако жица остане вертикална и ротира под неким углом око ове вертикалне осе? Чињеница је да се струја ни у једном случају не мијења. И даље иде право. Дакле, ова ротација не може да промени слику магнетног поља које се производи.

Структуре

Постоје само две могуце структуре које це од тога радити. Или су поља усмерена радијално према или од жице, или око жице. Прва могућност је да људи добију електрично поље из електрично набијене жице. Друга могућност је да можете добити магнетно поље које ствара струја кроз жице.

За једнооблично поље има кружне структуре у центру жице, а јачина поља се смањује са растојањем. Као узорак, веома је сличан таласима који се формирају када камен падне у воду. Постоје две главне разлике између рибњака и обрасца магнетног поља. Први је да магнетно поље остаје непромењено на датој удаљености. Она неће расти, али ће се смањити у датој тачки. Други је да магнетно поље има смер ка свакој тачки тангенције круга.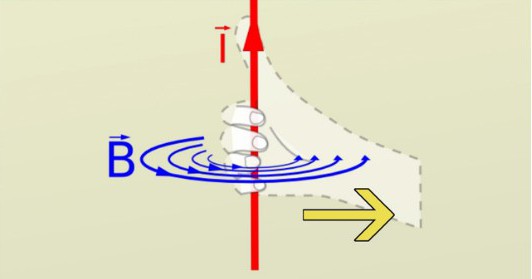

Струја и удаљеност

Следећи део Амперовог закона каже да јачина магнетног поља зависи од јачине струје и удаљености од жице. Резултат је да ако магнетно поље помножите за обод круга, овај производ ће бити пропорционалан снази електричне струје. То јест, ако удвостручите удаљеност од жице, линија обода се удвостручи, а магнитуда пада за 2 пута.

Али Амперов закон вам омогућава да се бавите струјама које се производе у системима сложенијим од једне жице. Али сви ови случајеви су еквивалентни. То значи да је идеја јачина магнетног поља умножена дужином пута остаје корисна и још увијек овиси о зброју свих струја унутар круга који формира путању.

Како можете разумети закон у практичном смислу?

То подразумева векторски рачун који се може објаснити на интуитиван начин:

• Магнетска поља стварају електричне струје.
• Магнетна поља су “рањена” на струји која их производи у датом правцу.
• Што је више струје, то је јаче магнетно поље створено. Јачина магнетног поља је пропорционална струји.

Амперов закон повезује ове концепте у једну од две математичке формуле. Поље постаје интензивније док се приближава жици.

Пропорционалност укупној струји

У интегралном облику Амперовог закона користи се концепт линеарног интеграла. У принципу, можете изабрати одређени циклус (тј. Затворени пут кроз простор) и ходати дуж петље, збрајати компоненте магнетног поља. Ово ће показати колико се магнетно поље окреће око површине која је ограничена петљом. Тврдња да је ова количина пропорционална укупној струји, која је ограничена петљом, је тачна.

Да бисте разумели ово, морате узети у обзир жицу која ограничава коло. Ако кружите око жице, магнетно поље увек иде у тачку у истом правцу, што значи да ће укупна сума кривочелног интеграла бити позитивна. Каже да можете ићи око струје! Поред тога, можете одредити смер струје користећи правило десне руке. Ако струја тече у другом правцу, вредност кривуље интеграла је инвертована.

Сада можемо претпоставити да се узима циклус у којем се не затвара жица, већ се преко жице прави круг супротно од казаљке на сату. Ако ходате око дна петље, у већини случајева правац ће ићи узводно, дакле допринос интегралу ће бити негативан. Али када смер прође око врха петље, у већини случајева то ће бити исто као и струја, тако да ће допринос бити позитиван. Каже да у циклусу нема ничега (или нема струје, или се струје у супротним правцима међусобно компензирају).

Дифферентиал

У диференцијалној форми примена Амперовог закона јавља се у концепту увојки векторског домена. Кривуља је квантитативна димензија, векторско поље је “увијање” око дате тачке. Ако узмемо мање и мање циклусе око тачке и израчунамо кривоцински интеграл, резултат треба да буде приближно пропорционалан површини петље. Коефицијент пропорционалности је увијен.

Ако узмете циклус који не садржи жице, интегрални правац ће увек бити нула. Ако се петља даље и даље, то ће увек бити нула. Коефицијент пропорционалности ће бити једнак нули, а ротор ће бити једнак нули (тачније, нулти вектор). Али ако сте унутар жице, онда без обзира на врсту петље, она ће примити струју која тече кроз њу. Идеја је да за бесконачно мали круг, само густина струје у овом тренутку ће бити „изнутра“ од ње, па ће само густина струје у овој тачки одредити вредност криволинијског интеграла. Дакле, ротор мора бити пропорционалан густини струје у датој тачки, јер је повезан са вредношћу кривочелног интеграла преко бесконачно мале петље.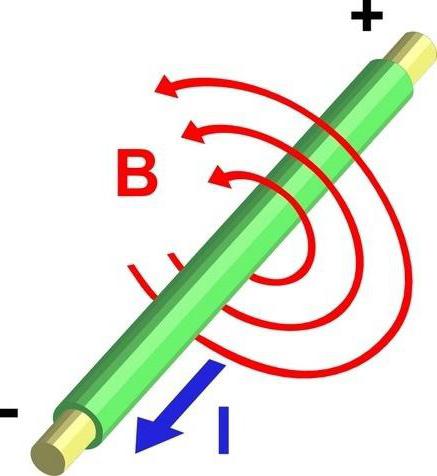

Закључак

У диференцијалним и интегралним формама, Амперов закон је еквивалентан и може се показати применом Стокесове теореме. У суштини, диференцијални облик је бесконачно мала верзија друге једнаџбе у "интегралном облику". Али Стокесова теорема је тема за другу студију.