Фибоначијев низ и принципи Златне секције
Фибоначијев низ, који је постао познат већини кроз филм и књигу Да Винцијеве шифре, је низ бројева изведених од стране италијанског математичара Леонарда из Пизе, познатијег под псеудонимом Фибонацци, у КСИИИ вијеку. Следбеници научника су приметили да формула којој је ова серија бројева подређена проналази свој одраз у свету око нас и резонира са другим математичким открићима, отварајући нам врата за тајне универзума. У овом чланку ћемо описати шта је Фибоначијев низ, размотрити примере мапирања овог обрасца у природи, и упоредити га са другим математичким теоријама. 
Формулација и дефиниција
Фибоначијев низ је математичка секвенца, чији је сваки елемент једнак збиру претходна два. Нека неки члан секвенце буде кн. Тако добијамо формулу која је валидна за целу серију: кн + 2 = кн + кн + 1. Са овим редослед редоследа ће изгледати овако: 1, 1, 2, 3, 5, 8, 13, 21, 34. Следећи број ће бити 55, јер је сума од 21 и 34 55. И тако даље по истом принципу.
Ad
Примери у окружењу
Ако погледамо биљку, посебно на круну лишћа, напомињемо да они цветају спирално. Углови се формирају између сусједних листова, који, са своје стране, формирају исправан математички Фибоначијев низ. Захваљујући овој функцији, сваки појединачни лист који расте на дрвету прима максималну количину сунчеве светлости и топлоте. 
Фибонацци Матх Пуззле
Чувени математичар је своју теорију представио као загонетку. Звучи на следећи начин. Можете ставити пар зечева у затворени простор како бисте сазнали колико ће се парова зечева родити у року од једне године. С обзиром на природу ових животиња, чињеница да је сваки мјесец пар способан да произведе нови пар, а спремни су за размножавање након два мјесеца, на крају је добио свој познати број бројева: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144 - где је приказан број нових парова зечева у сваком месецу.
Ad
Фибоначијев низ и пропорционални однос
Ова серија има неколико математичких нијанси које свакако треба узети у обзир. Он, који се приближава спорије и спорије (асимптотски), тежи неком пропорционалном омјеру. Али то је ирационално. Другим речима, то је број са непредвидивим и бесконачним низом децималних бројева у фракцијском делу. На пример, однос било ког елемента из серије варира око броја 1.618, а затим превазилази, а затим достиже. Следеће по аналогији се приближава 0.618. Оно што је обрнуто пропорционално броју 1.618. Ако поделимо елементе кроз један, добићемо 2.618 и 0.382. Као што сте већ разумели, они су такође обрнуто пропорционални. Добијени бројеви се називају Фибоначијеви коефицијенти. А сада ћемо објаснити зашто смо извршили ове калкулације. 
Голден ратио
Разликујемо све објекте око нас према одређеним критеријумима. Једна од њих је форма. Неки од нас привлаче више, неки мање, а неки не воле. Примећено је да је симетрични и пропорционални објект много лакше перципиран од стране човјека и изазива осјећај хармоније и љепоте. Цела слика увек укључује делове различитих величина који су у одређеном међусобном односу. Отуда и одговор на питање шта се зове Златни одељак. Овај концепт подразумева савршенство односа између целине и делова у природи, наука, уметност и Од математичке тачке гледишта, размотрите следећи пример. Узмите сегмент било које дужине и поделите га на два дела тако да се мањи део односи на већу као на суму (дужину целог сегмента) на већу. Дакле, узимамо сегмент ц за вредност једне. Његов део а биће једнак 0.618, други део б , испада, је једнак 0.382. Дакле, ми се држимо услова Златног Одсека. Однос сегмента ц на а једнак је 1.618. А однос делова ц и б је 2.618. Добили смо Фибоначијеве коефицијенте који су нам већ познати. По истом принципу граде се златни троугао, златни правоугаоник и златни квадар. Такође је вредно напоменути да је пропорционални однос између делова људског тела близак Златном омјеру. 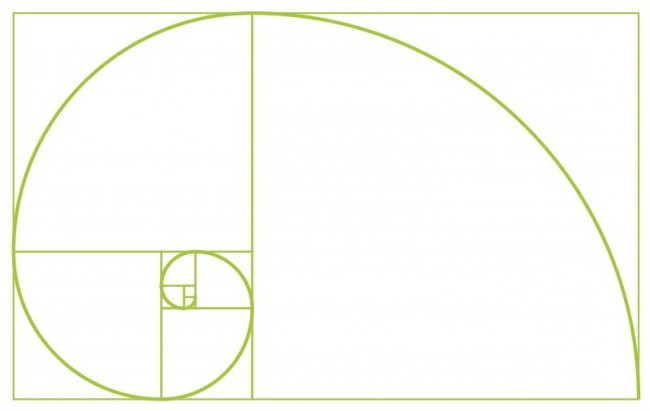
Да ли је Фибоначи низ основа за све?
Покушајмо да комбинујемо теорију Златне секције и чувене серије италијанских математичара. Почнимо са два квадрата прве величине. Затим на врх додамо још један квадрат друге величине. Хајде да нацртамо поред исте фигуре са дужином стране која је једнака збиру две претходне стране. На сличан начин нацртајте квадрат пете величине. И тако можете наставити бесконачно дуго док вам не буде досадно. Главна ствар је да је величина стране сваког следећег квадрата једнака збиру вредности страна два претходна. Добили смо низ полигона чија је дужина Фибоначијеви бројеви. Ове бројке се зову Фибоначијеви правоугаоници. Хајде да нацртамо глатку линију кроз углове наших полигона и добијемо ... Архимедову спиралу! Повећање висине ове фигуре, као што знате, је увек униформно. Ако укључите фантазију, тада се слика може повезати са шкољком. Из овога се може закључити да је Фибоначијев низ основа пропорционалних, хармоничних односа елемената у околном свету. 
Математичка секвенца и универзум
Ако боље погледате, онда Архимедова спирала (негде експлицитно, али негде прикривено) и, према томе, Фибоначијев принцип може се пратити у многим уобичајеним природним елементима који окружују особу. На пример, исту шкољку шкољки, цветове брокуле, цвет сунцокрета, конус четинарске биљке и слично. Ако погледамо у страну, видећемо Фибоначијев низ у бескрајним галаксијама. Чак и особа, надахнута природом и усвајајући њен облик, ствара објекте у којима се може пратити поменута серија. Сада је време да се присетимо Златне секције. Заједно са Фибоначијевим обрасцем, прате се принципи ове теорије. Постоји верзија да је Фибоначијев низ врста теста природе који се прилагођава савршенијој и темељној логаритамској секвенци Златног одељка, који је готово идентичан, али нема почетка и бесконачан је. Природа природе је таква да мора имати своју полазну тачку, од које треба градити да би створила нешто ново. Однос првих елемената Фибоначијевог низа је далеко од принципа Златне секције. Међутим, што даље настављамо, то се више распарчава. Да би се одредила секвенца, неопходно је знати њена три елемента који слиједе један за другим. За Златну секвенцу, два су довољна. Пошто је и аритметичка и геометриц прогрессион.
Закључак
Ипак, на основу горе наведеног, можете поставити прилично логична питања: "Одакле долазе ови бројеви? Ко је аутор читавог свијета који је покушао да га учини савршеним? Да ли је све увијек било онако како је желио? Ако је тако, зашто је пропао?" Шта ће се даље десити? " Проналажење одговора на једно питање добија се следеће. Решио сам - још два се појављују. Након што сте их решили, добићете још три. Након што сте се позабавили њима, добићете пет неријешених питања. Онда осам, тринаест, двадесет један, тридесет четири, педесет пет ...