Метода коначних елемената и њена примена
Метода коначних елемената појавила се као једна од техника за проучавање различитих дизајна. Тренутно је универзално препознат као заједнички начин рјешавања широког спектра задатака у различитим областима технологије.
Дефиниција
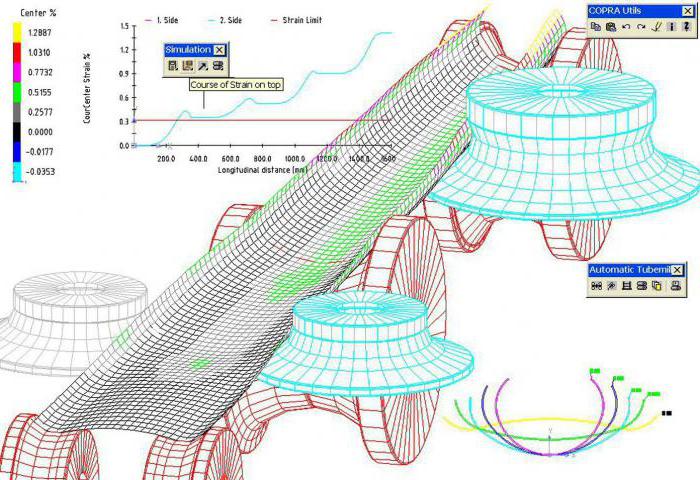
Инжењерска анализа методом коначних елемената састоји се у апроксимацији континуираног медија са бесконачно великим бројем степена слободе помоћу скупа елемената (поддомена) који имају коначне бројеве степена слободе. Успостављен је однос између ових елемената. Препознавање методе објашњава се једноставношћу математичког облика и физичке интерпретације.
Користи се у механици
Метода коначних елемената у механици лома и проблемима структурне механике изражава се као однос МКЕ у облику помака. Прво, тзв. Функције форми се постављају унутар сваког елемента. Они дефинишу кретање у унутрашњем подручју елемента покретом у чворовима. Ово су тачке у којима су комбиновани коначни елементи.
Непознате МКЕ су могући и независни покрети чворова модела коначних елемената (ЦЕМ). Тако је КЕМ дизајн систем фиксних чворова. Додатне везе корелирају са правцем могућих кретања чворова.
Суштина методе
У основи, елементарни модел дизајна је сличан основном систему класичне методе померања, која се користи у прорачуну система шипки. Да би се постигла пријемна тачност резултата прорачуна помоћу методе коначних елемената, потребно је смањити величину елемената, чиме се повећава тачност апроксимације геометријских карактеристика и функција помака унутар коначног елемента.
Комплексне структуре ЦЕМ-а достижу стотине или чак милионе степени слободе, па је метода коначних елемената у инжењерству оријентисана на машину, чија је реализација могућа само помоћу рачунара.
Практична имплементација
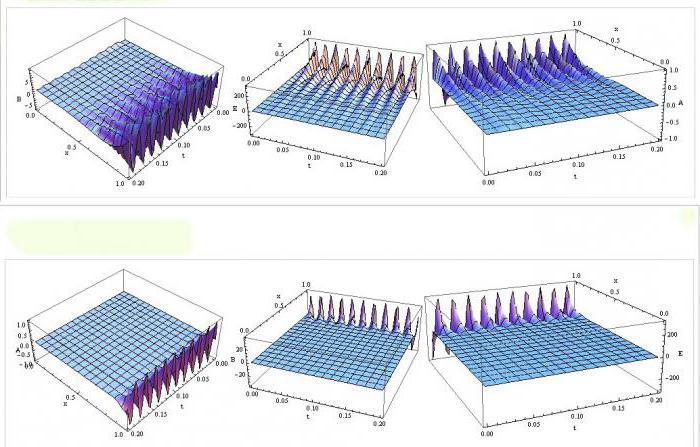
Да би се ФЕМ применила у пракси, потребно је разумети не само теорију механике, већ и познавање програмирања. Примена методе коначних елемената често се заснива на варијационим принципима механике, који се заснивају на два фундаментална скалара: потенцијал и кинетичка енергија еластична конструкција. Дефиниција ових скалара, независна од изабраног координатног система, дозвољава да се пише релација МКЕ у инваријантном облику.
Ради лакшег програмирања, ФЕМ омјери се биљеже у компактном матричном или тензорском облику. Тренутно је симулација методом коначних елемената потпуно математички поткрепљена, стварају се софтверски производи високих перформанси, који се стално побољшавају заједно са програмским алатима.
Образовни програми
Технички напредак, посебно у области рачунара, значајно је променио ставове о формулацији и решавању инжењерских проблема. Конструкција рачунског модела је уско повезана са процесом рачунања и готово је немогуће раздвојити ове две фазе на путу добијања практичних резултата.
Метод коначних елемената је у широкој употреби у инжењерској пракси, што је такође допринело његовом укључивању у наставне планове и програме универзитета. ФЕМ нуди начине да се изгради математички модел феномена који се разматра, на основу његове физичке суштине.
Први уџбеници о МКЕ писани су на сложеном језику, али су ускоро поједностављене методе подучавања захваљујући увођењу специјализованих програма. На пример, софтверски пакет Ассистант се добро показао. Омогућава тестирање знања студената на мрежи и доприноси развоју вештина рада са софтверским производима у решавању практичних проблема.
Прорачун линеарних деформација
Данас се основе методе коначних елемената заснивају на чињеници да вриједности и концепти својствени њој нису унапријед представљени, већ произлазе из суштине проблема структурне механике. Распон проблема који се могу ријешити уз помоћ ФЕМ-а је готово неограничен. Размотримо, на пример, проблем израчунавања линеарне деформације еластичних структура од дејства статичких оптерећења.
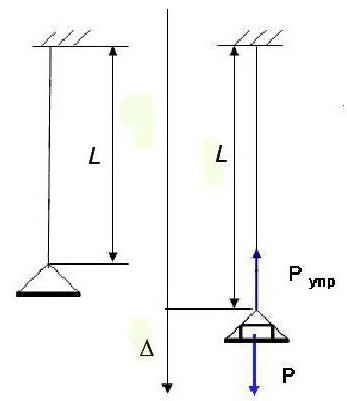
Енглески физичар Р. Хооке спровео је истраживање о деформацијама централно оптерећених шипки направљених од различитих еластичних материјала под дејством статичке силе: Пл = Пл / ЕА.
Такође је утврдио везу између величина које одређују овај процес: σ = Еε, где је деформација изражена односом ε = ∆ / л, напон је означен као σ = П / А (овде А је површина попречног пресека штапа).
Коефицијент пропорционалности Е одређује еластичне карактеристике материјала и има физичку суштину - напрезање које одговара јединичном напрезању.
Утицај статичке силе
Статички дјелујућа сила постепено расте с временом (Г≥П≥0). Покрети које генерише такође расте постепено, без убрзања.
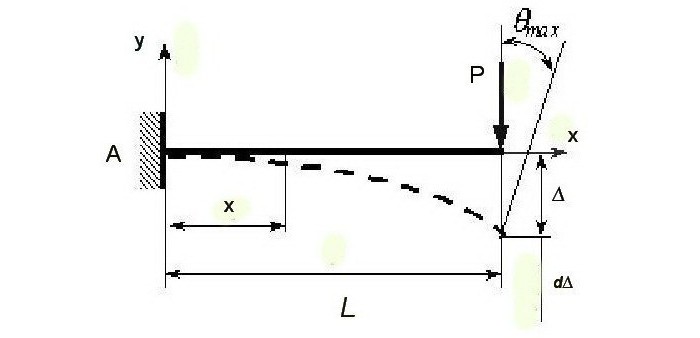
Анализа методом коначних елемената омогућава нам да одредимо ефекат статичке силе на померање, с обзиром да се ови индикатори разликују. Повећање (повећање) на снази на бесконачно малој вредности дП одговара повећању (повећању) помака д∆. Радна снага (П + )П) на помаку д∆ је дА = (П + )П) × д∆.
Коначна вредност радне снаге одређена је формулом А = Пд∆.
Уведимо однос димензионалних варијабли под знаком интеграла ∆ = Пα, гдје је α коефицијент усклађености, који изражава физичку суштину помицања точке у коју се додаје јединична сила у смјеру те силе. Однос П = Пα поставља јединицу мере α (м / Н). Из тога следи да је д∆ = дПα.
Коефицијент усаглашености одговара другој важној карактеристици конструкције - коефицијенту крутости к = л / α (н / м), који одређује силу која изазива појединачно кретање конструкције у правцу те силе.
Узимајући у обзир све карактеристике и коефицијенте, коначна једначина има облик: А = ПдПα = α × (П 2/2) = (Г∆) / 2.
Добијена је Цлапеирон формула, која одређује стварни рад статички дјелујуће силе на помаку, коју је сама генерирала у еластичном тијелу. Друге нумеричке методе су израчунате помоћу ове технике.
Метод коначних елемената за барске системе
Шипка је просторно тијело, од којих су двије величине, ширине и висине, много мање од дужине. То омогућава да се његов физички модел посматра у виду линије која пролази кроз центре секција. Ако се спољашње силе које се примењују на шипку налазе у истој равни са њеним моделом, онда можемо претпоставити да се његове деформације дешавају у истој равни.
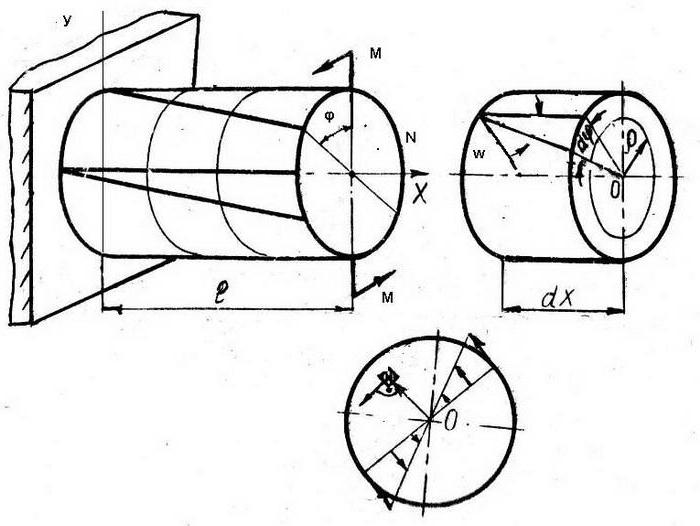
Са математичке тачке гледишта, геометријске карактеристике помака и напрезања унутар шипке су функције истог аргумента. Односи теорије еластичности заснивају се на хипотези о равним секцијама шипке. Однос између деформација и напрезања одговара линеарном Хооковом закону. У сваком делу шипке појављују се три равни кретања:
- у координата је уздужна сила;
- координата в - отклон;
- координата англе - угао ротације.
У овом случају, уздужни у и прогиб в су независни, а угао ротације изражава се формулом д = дв / дк, гдје је дв количина отклона након примјене вањске силе на шипку, дк је сегмент отклона (одређен вриједношћу в + дв).
За бесконачно мали штап дк, однос дк = дφ × П је валидан.
Потенцијална енергија Деформације шипки се природно рачунају у локалном координатном систему чија к оса се поклапа са осом штапа, а оса и је окомита на ос стазе: У = ½∫Н × ду + ½∫М × дφ = ½∫Н × (ду / дк) дк + ½ × × (ду / дк) дк + ½ ×М × (д²в / дк²) дк.
Исопараметарски приступ у МКЕ
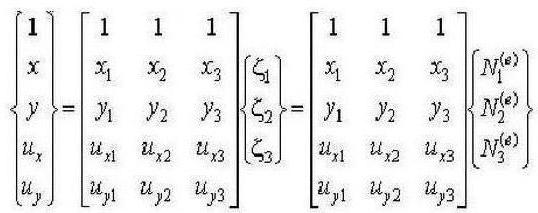
Размотримо примену методе коначних елемената у изопараметријском систему коначних елемената структуре под напоном равнине. Процес стварања модела коначних елемената састоји се од неколико фаза, од којих је прва конструкција мреже коначних елемената (ФЕ), избор глобалног координатног система у односу на целу структуру и локални систем повезан са коначним елементом.
Кључни корак је дефинисање функција форме, које обезбеђују дефиницију померања унутар коначног елемента услед кретања њених чворова. Постоје различити начини конструкције функција једног облика, али они морају осигурати испуњење неколико услова за апроксимацију функција помака.
- Испуњење континуитета помака не само на чворовима коначних елемената, већ и на њиховим границама.
- Обезбеђивање очувања дериватних функција померања које се односе на еластични потенцијал.
- Кретање коначног елемента као крути број. То значи да када се елемент помакне као крута твар, компоненте вектора деформације су нуле.
Проблеми и решења
Теорија метода коначних елемената наводи да се ФЕМ односи формирају у локалном координатном систему. Стога се наведени захтјеви за функције формата изводе аутоматски ако су оси локалног система оријентиране дуж страница коначног елемента. Такви случајеви се дешавају за коначне елементе језгрене структуре, правокутне зидне плоче и правокутне плоче.
Али у пракси постоје конструкције са контурама произвољне дефиниције. У овом случају потребно је извршити трансформацију за апроксимацију помака у глобалном координатном систему, што доводи до дисконтинуитета помака на границама коначних елемената и, као резултат, до губитка тачности приближних прорачуна.
Настала је идеја да се на квадрат са локалним координатним системом, чије је поријекло у центру ове фигуре, и оси оријентисане на његове стране, прикаже раван, четверокутан коначни елемент општег облика. За даљу употребу коначних елемената у облику квадрата потребно је успоставити везу један-на-један између локалних координата произвољног четверокута ФЕ и локалног координатног система ФЕ у облику квадрата. За квадратни коначни елемент, заправо, функције форме се конструишу прилично једноставно.
Метода коначних елемената за прорачуне плоча
Плоча је уметак или цилиндрично тело чија је висина много мања од величине у плану. Висина се зове дебљина плоче. Равнина која дели висину плоче на пола се зове средња или референтна равнина. Линија пресека бочне површине са средњом равни се назива контура плоче.
Сматра се да је танка плоча, за коју је однос дебљине према мањој величини у плану унутар х≤Л / 5, гдје је х дебљина плоче, Л је његова ширина.
Плоча се сматра крутом ако, под дејством попречног оптерећења, њен највећи отклон током деформације не прелази 1/5 њене дебљине.
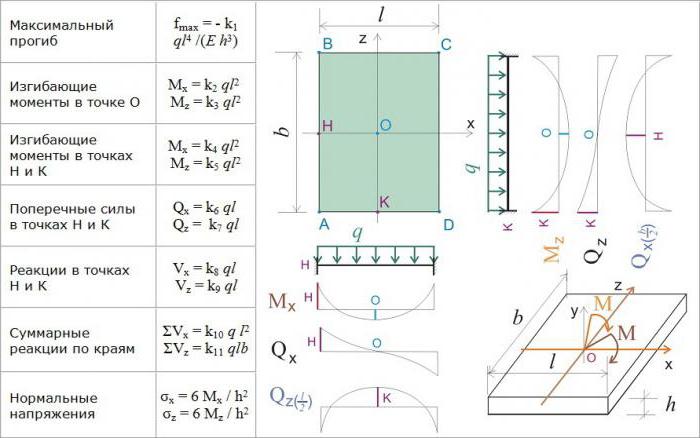
Приликом рачунања по методи ФЕ, прво се уноси координатни систем: Кс 1 , Кс 2 и Кс 3 . Почетак оси Кс 1 и Кс 2 налази се у средњој равнини. Оса Кс 3 је оријентисана уздуж нормале до средње оси.
Прорачуни се обично своди на рачунање помака (помака) плоче у одређеној тачки под утицајем оптерећења (сила). На произвољној тачки плоче, која се сматра тродимензионалним телом, појављују се три правца кретања: У 1 , У 2 , У 3 . Дефиниција је кретање дуж нормале на средњој равни, која се назива прогиб и означена је словом В.
Сматра се да су прорачуни изведени ако се из датог оптерећења (а то је обично равномјерно распоређено, усмјерено на површину), утврди метода за израчунавање помака У и помака В у произвољној точки плоче. ФЕМ односи се заснивају на одредбама техничке теорије еластичности коју је предложио физичар Кирцххофф.
Кирцххоффове хипотезе
Метода коначних елемената је у великој мери заснована на хипотезама које је 1845. формулисао немачки физичар Г. Киргхофф. Изравна нормална хипотеза наводи да свака праволинијска нормална линија до средње равнине недеформисане плоче остаје равна и нормална до средње површине деформисане плоче, а дужина праве линије се не мења. Његова суштина је у одсуству промене између слојева плоче у дебљини.
Ако су оси картезијанских координата постављене тако да се равнине Кс 1 , Кс 2 подударају са средњом равни, онда следе прве једнакости из првог дела хипотезе: и 13 = 0, и 23 = 0. Хипотеза о непроменљивости дужине праве линије претпоставља да је линеарна деформација у правцу осе Кс 3 нула: ε 33 = 0.
Хипотеза о одсуству притиска између слојева плоче паралелно са средњом површином сугерише да се напони σ33 у односу на напрезања σ11 и σ22 могу занемарити, односно σ 33 = 0.
Хипотеза о не-деформабилности средње равни сугерише да у средњој равни плоче нема деформација напетости, компресије и смицања. То јест, средња раван је неутрална. Тако је у њему помак У 1 = У 2 = 0.
Закључак
Метода коначних елемената, која се широко користи у конструкцији и механици, омогућава израчунавање помака различитих елемената подвргнутих одређеним оптерећењима. Систем, који су 1936. године формулисали совјетски научници, почео је да се широко користи тек деценијама касније, јер је захтијевао велику количину прорачуна. Увођењем рачунара овај задатак је поједностављен.