Потпуно убрзање и његове компоненте. Тангенцијално убрзање и нормално убрзање. Формуле и пример решавања проблема
У кинематици, да би се недвосмислено одредиле карактеристике кретања тела у било којој тачки путање, неопходно је знати њену брзину и убрзање. Временска овисност ових количина даје све потребне информације за израчун путање које путује тијело. Размотримо детаљније у чланку шта је тангенцијално убрзање и нормално убрзање.
У физици
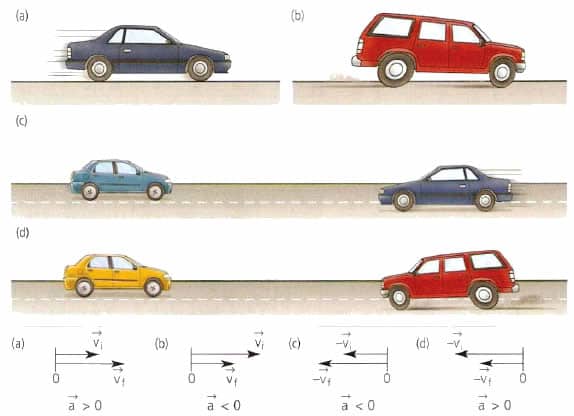
Пре разматрања убрзања за механичко кретање, нормално и тангенцијално убрзање, упознајмо се са физичким концептом. Дефиниција убрзања је прилично једноставна. У физици, под њим разумију карактеристичну промену брзине. Ово последње је векторска величина која одређује брзину промене координата покретног објекта у простору. Брзина се мјери у метрима у секунди (пређена удаљеност по јединици времена). Ако је означено симболом в¯, онда ће математичка дефиниција убрзања а¯ изгледати овако:
а¯ = дв¯ / дт
Ова једнакост дефинира такозвано пуно тренутно убрзање. Назива се инстант, јер карактерише промену брзине само у одређено време.
Ако је кретање једнако убрзано, дакле, дуго времена, убрзање не мења свој модул и смер, онда можемо написати следећу формулу да бисмо је одредили:
а¯ = Δв¯ / Δт
Где Δт >> дт. Вредност овде се назива просечно убрзање, које се генерално разликује од тренутног.
У СИ систему се мери убрзање у метрима по квадратном секунди (м / с 2 ).
Трајекторија и компоненте пуног убрзања
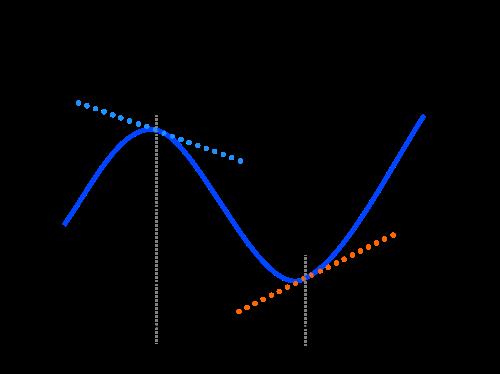
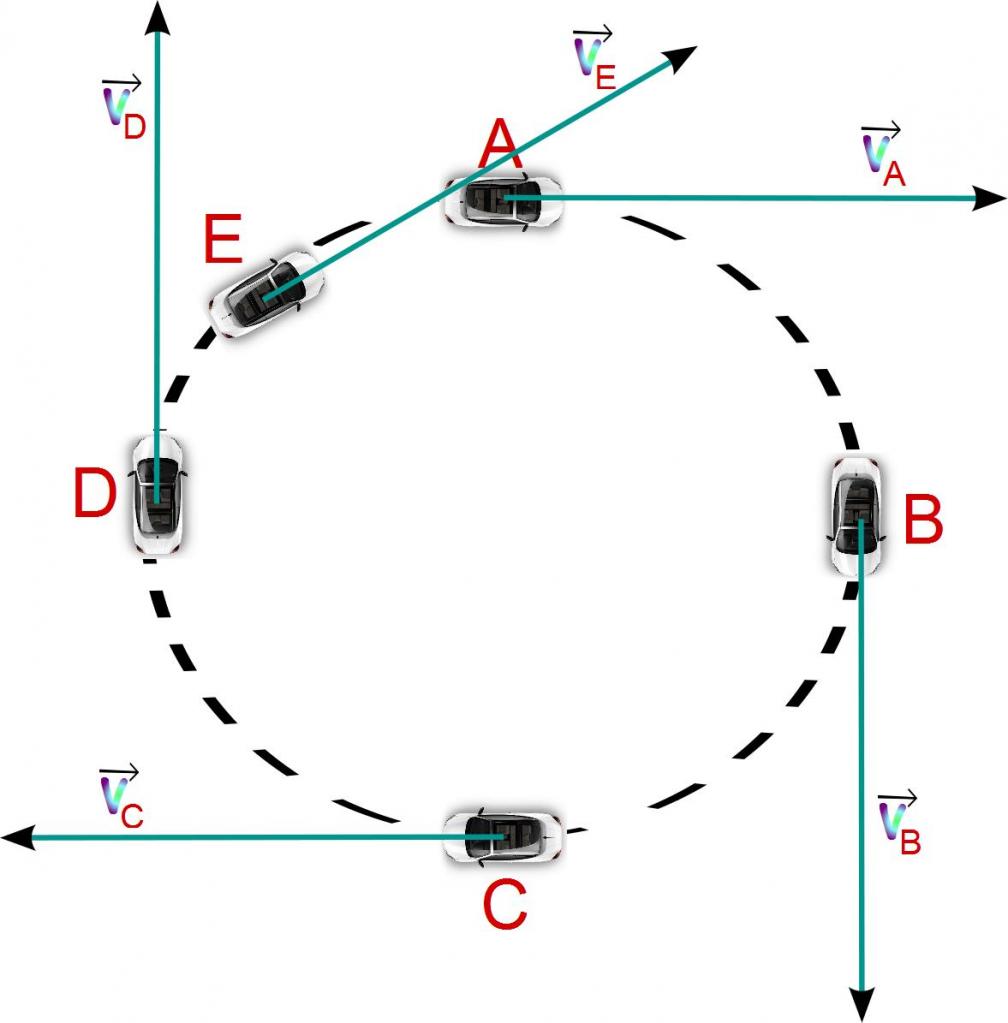
Најчешће се тијела у природи крећу уздуж закривљених путања. Примери таквог кретања су: ротација планета у њиховим орбитама, параболични пад камена на земљи, окретање аутомобила. У случају кривуље путање у било ком тренутку, брзина је усмерена тангенцијално на тачку путање у питању. Како се усмерава убрзање?
Да бисмо одговорили на претходно питање, пишемо брзину тела у следећем облику:
в¯ = в * у т ¯
Овде, у т ¯ је вектор јединичне брзине, индекс т значи да је усмерен тангенцијално на путању (тангенцијална компонента). Симбол в означава модул брзине в.
Сада, слиједећи дефиницију убрзања, можемо разликовати брзину у односу на вријеме, имамо:
а¯ = дв¯ / дт = дв / дт * у т ¯ + в * д (у т ¯) / дт
Дакле, укупно убрзање а¯ је векторска сума од две компоненте. Први и други израз се називају нормално и тангенцијално убрзање тачака. Погледајте ближе сваку од ових компоненти.
Тангенцијално убрзање
Још једном напишемо формулу за ову компоненту пуног убрзања:
а т ¯ = дв / дт * у т ¯
Овај израз нам омогућава да опишемо својства т ¯:
- Усмерена је на исти начин као и сама брзина или супротно од ње, тј. Дуж тангенте трајекторије. О томе сведочи елементарни вектор у т ¯.
- Она карактерише промену брзине у апсолутној вредности, која се рефлектује фактором дв / дт.
Ова својства нам омогућавају да направимо важан закључак: за правоцртно кретање, пуна и тангенцијална убрзања су исте вредности. У случају закривљеног кретања, укупно убрзање је увијек веће величине од тангенцијалне. Када се разматрају физички задаци за правоцртно равномерно убрзавање кретања, они говоре о овој компоненти убрзања.
Убрзање нормално
С обзиром на тему брзине, убрзања тангенцијалног и убрзања нормале, дајемо опис задње вриједности. Пишемо формулу за то:
а н ¯ = в * д (у т ¯) / дт = в * д (у т ¯) / дЛ * дЛ / дт
Да експлицитно напишемо десну страну једнакости, користимо следеће односе:
дЛ / дт = в;
д (у т ¯) / дЛ = 1 / р
Овде је дЛ удаљеност коју је тело превалило током временског интервала дт, р је радијус закривљености путање. Први израз одговара дефиницији брзине, друга једнакост слиједи из геометријских разматрања. Користећи ове формуле добијамо коначни израз за нормално убрзање:
а н ¯ = в 2 / р
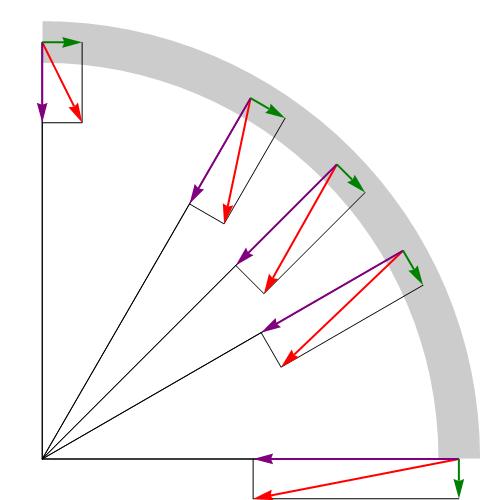
Односно, вредност а н ¯ не зависи од промене брзине, као тангенцијалне компоненте, већ се одређује искључиво њеним модулом. Нормално убрзање дуж нормале до овог дијела путање је усмјерено, тј. Према средишту закривљености. На пример, док се креће дуж круга, вектор а н ¯ је усмерен ка његовом центру, тако да се нормално убрзање често назива центрипетал.
Ако је убрзање тангенцијално за промену величине брзине, онда је нормална компонента одговорна за промену вектора брзине, односно, одређује путању тела.
Пуно, нормално и тангенцијално убрзање
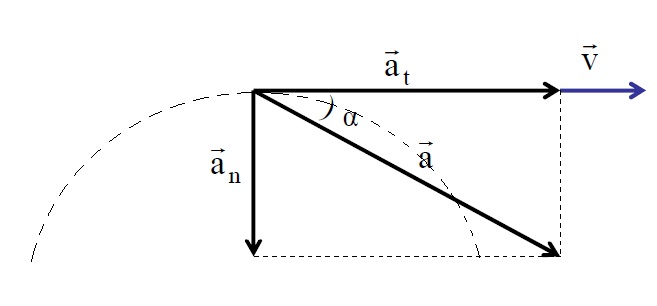
Радећи по концепту убрзања и његових компоненти, сада дајемо формулу која нам омогућава да одредимо пуно убрзање. Пошто су разматране компоненте усмерене једна на другу под углом од 90 о , Питагорина теорема се може користити за одређивање апсолутне вредности њихове векторске суме. Формула за потпуно убрзање је:
а = √ (а т 2 + а н 2 )
Правац величине а може се одредити у односу на вектор било које од компоненти. На пример, угао између а и н ¯ израчунава се као:
θ = арцтан (а т / а н )
Узимајући у обзир горњу формулу за модул а, можемо закључити: са равномерним кретањем дуж круга, пуно убрзање се поклапа са центрипеталним.
Решавање проблема
Нека се тело креће у кругу полупречника од 1 метра. Познато је да његова брзина варира у складу са следећим законом:
в = 2 * т 2 + 3 * т
Потребно је одредити тангенцијално убрзање и нормално убрзање у тренутку т = 4 секунде.
За тангенцијалну имамо:
а т = дв / дт = 4 * т + 3 = 19 м / с 2
Да бисте пронашли нормални модул убрзања, прво морате израчунати вриједност брзине у одређеном временском тренутку. Имамо:
в = 2 * 4 2 + 3 * 4 = 44 м / с
Сада можете користити формулу за н :
а н = в 2 / р = 44 2/1 = 1936 м / с 2
Тако смо одредили све количине које су биле потребне да би се проблем ријешио.