Како пронаћи волумен коцке: опције за проблеме и њихово рјешење
Модерне технологије стварају невероватне рачунарске програме. Они вам омогућавају да видите тело у волумену и да их окренете у различитим правцима како бисте добили бољи изглед. Човјекова машта није увијек способна за то. Мало ко може јасно да представи тему и да је види. Међутим, таква вјештина се може покушати формирати при рјешавању проблема у геометрији. На пример, они који говоре о томе како да нађу волумен коцке. Ово је одлична пракса за развој просторне имагинације.
Коцка или паралелепипед?
Ово је питање које није празно. Зато што је класификација важна. На крају крајева, коцка је посебан облик правокутног паралелепипеда.
Ово последње је фигура у којој има 6 лица, а сви су они правоугаоници. Кутови на којима се све ивице секу, 90º. Сходно томе, ако ова лица постану квадрати, онда ће се цела фигура трансформисати у коцку.

У правокутном паралелопипеду, све линеарне димензије, тј. Висина, дужина и ширина, могу се значајно разликовати. У коцки су увек једнаке једна другој. То је њен заштитни знак. Дакле, у задацима који захтевају одређивање запремине коцке, у обзир се свакако узима и разматрани момент. Успут, то увелико поједностављује све математичке записе и прорачуне.
Конвенције у формулама и проблемима
Без ове ставке биће тешко разумети како су формуле написане. Оно што се подразумева под сваким словом и симболом, захтева следећу табелу.
| Симбол | Назив ставке |
| а | облик ребра |
| д | дијагонално лице |
| Д | дијагонална коцка |
| заједнички геометријски симболи | квадрат |
| волумен |
Како пронаћи елементе коцке на његовој страни?
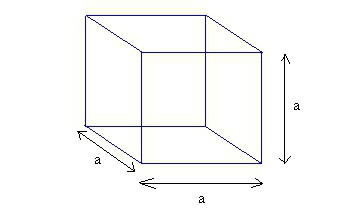
Пошто је лице фигуре квадрат, његова површина је одређена формулом бр. 1, у којој се позната вредност мора квадрирати:
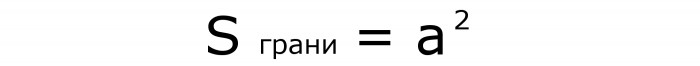
И дијагонала било којег лица се израчунава по формули бр. 2, у којој се страна множи са кореном од 2:
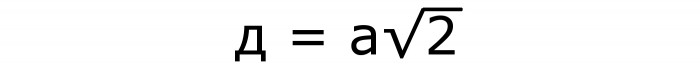
Претходна формула је добијена из Питагорине теореме. Ово је лако разумети ако видите да је дијагонала лица хипотенуза правоугаони троугао. А стране трга постају његове ноге.
Да би се одредила дијагонала коцке, потребна је следећа формула бр. 3, која садржи познату страну и скуаре роот од 3:
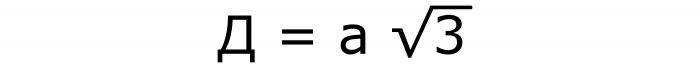
Она се добија и из Питагорине теореме. Само као хипотенуза дјелује жељена дијагонала. Са стране квадрата и његовом дијагоналом постају ноге.
Понекад морате знати формулу за израчунавање површине бочне површине ове фигуре. У њему, квадрат стране се множи са 4. Овде је (бр. 4):
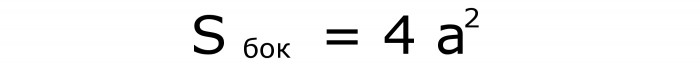
Разумевање начина на који ова формула функционише је лако. Постоје 4 бочна лица - 4. То значи да је њихова укупна површина четверострука вриједност површине једног квадрата.
Ако је потребно да одредите површину целокупне површине , користите овај запис, у коме се тргује квадратом ребра (формула бр. 5):
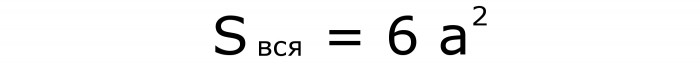
Добија се слично претходној формули, само број квадрата је повећан на 6.
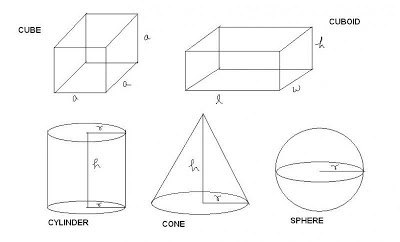
Шта је волумен?
Једноставно речено, ово је место које узима свако тело у простору. Сваки простор је ограничен у простору површинама. Може их бити више, али може бити случајева када је само један. На пример, ако је тело лопта. Али ове површине су нужно затворене. Простор који заузима геометријско тијело ће бити његов капацитет или волумен.
Јединице волумена
Када су у питању чврсте материје, јединице волумена ће увијек бити кубне вриједности. На пример, метар, центиметар или километар у коцки. За течности се користе литри, изражени у кубним дециметрима. Али ако заузимају велике количине, мере се и у кубним метрима. На пример, када се узме у обзир потрошња воде у стану, она се узима у м 3 . Тако се испоставља да је то практичнији и лакши у нумеричком смислу.
Метод 1: пронађите волумен коцке, ако је позната страна
Ово је најлакши начин да вам кажем како да нађете волумен коцке. То је једноставно да се подигне вредност партије до трећег степена. Другим речима, потребно је да три пута умножите страну. По аналогији са произвољним правокутним паралелепипедом, када је било потребно множити све њене линеарне димензије. Формула ће бити написана на следећи начин (# 6):
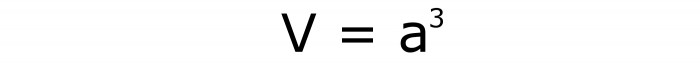
Метод 2: цијела површина је позната
У овом случају, потребно је подијелити познату вриједност са 6. Из интерног одговора, извадите квадратни коријен и подигните број на коцку. Ако напишемо ову формулу, добијамо следеће (# 7):
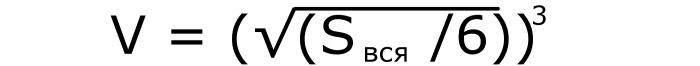
Метод 3: дати дијагонално лице коцке
Да бисте сазнали како да израчунате запремину коцке, у овом случају морате да извршите следеће кораке. Прво, изградите познату вредност у коцку, а затим је помножите са квадратним кореном од 2 и поделите са 4. Формула за овај проблем (бр. 8):
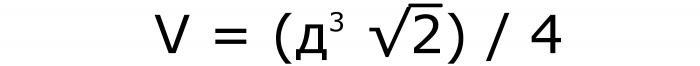
Ова једначина се добија на овај начин: позната дијагонала мора бити подељена кореном два. Затим, направите број до трећег степена. Након извршених трансформација, у нумератору се добија коцка дијагонале, а 2√2 у имениоцу. Математика захтева да не постоји ирационалан број испод линије. Дакле, они га се решавају множењем са .2. Тада се атор2 појављује у бројнику, а 4 се добија у имениоцу.
Метод 4: Коцка дијагонала
Формула која вам каже како да нађете волумен коцке ће садржати акције: квадрирање дијагонале, помножавање са кореном од 3, и дељење са само 9. То ће бити написано овако (бр. 9):
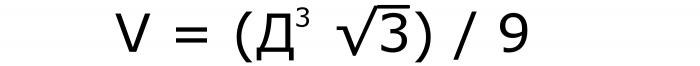
Слично претходној формули, у овом запису дијагонала је прво подељена у корен од три и подигнута на коцку. Након трансформација у називнику, појављује се и ирационалност, из које је потребно напустити. Тако се вредност аппеарс3 појављује у бројнику, а испод линије - 9.
Примери задатака
Задатак један. Дати је коцка са рубом од 12 цм, израчунати њен волумен и изразити одговор у квадратним метрима.
У овом задатку ће бити теже превести одговор у друге јединице него одлучити како пронаћи волумен коцке. Да бисте довршили први дио задатка, требат ће вам формула написана под бројем 6. Након што је број 12 уграђен у коцку, одговор ће бити 1728 цм3. Сада морамо да се сетимо како да их преведемо у кубне метре. У ту сврху, одговор мора бити подијељен на 100 три пута. Стотину је дошло из чињенице да је била стотињак центиметара на један метар. А подела се изводи три пута, јер су јединице у задатку кубне. Дакле, 1728 подељено са 100 дат ће 17.28. После друге дивизије биће 0.1728. Трећа акција ће дати одговор 0,001728 м 3 . Ово је одговор на проблем: волумен коцке је 0,001728 м 3 .
Задатак два. Постоји коцка са површином цијеле површине једнака 600 дм 2 . Пронађите волумен облика и изразите га у кубним метрима.
Да бисте одговорили на питање о овом задатку, биће потребна формула број 7. Прва акција је познати број подељен са 6. Одговор даје 100. Лако је извадити квадратни корен из њега, то ће бити 10. Сада треба да изградите првих десет у коцки. Тако се испоставља да је жељена вредност једнака 1000 дм 3 . Остаје да се претвори у м 3 . Као иу претходном задатку, подјела ће се извршити три пута, само ће дјелитељ бити 10. Јер има десет дециметара у једном метру. Након подјеле, одговор је 1 м 3 . Одговор: волумен је 1 м 3 .
Трећи задатак. Добијена је коцка са дијагоналном дужином лица од √2 мм. Потребно је израчунати јачину звука.
Осма формула ће помоћи у проналажењу одговора у овом проблему. Прва ствар коју требате направити је коцка познате вриједности. Квадратни корен од 2 у трећем степену ће дати вредност 2√2. Након множења са ,2, добијамо број 4. Последња акција је да се подели на 4. Одговор: волумен коцке је 1 мм3.
Четврти задатак. Познато је да је дијагонала коцке 3 м. Потребно је израчунати њен волумен.
Одговор на овај проблем биће лако пронаћи помоћу формуле број 9. Вредност дата у стању мора бити подигнута на коцку. Испада 27. Након што га поделимо на 9, одговор ће бити 3. А последња акција треба да се помножи са квадратним кореном од 3. Одговор проблема ће бити 33 м 3 .