Изобарни процес, сродне једначине и извођење формуле рада

Изобарни процес (који се назива и изобарички процес) један је од термодинамичких процеса који се јављају при константном индикатору притиска. Маса гасног система истовремено остаје константна. Визуелни приказ графикона који приказује изобарични процес дат је термодинамичким дијаграмом у одговарајућем координатном систему.

Примери

Најједноставнији пример изобарног процеса је загревање одређене количине воде у отвореној посуди. Као још један пример, може се дати експанзија идеалног гаса у цилиндричном волумену, где клип има слободан ход. У сваком од ових случајева притисак ће бити константан. Он је једнак обичном атмосферском притиску, што је сасвим очигледно.

Реверзибилност

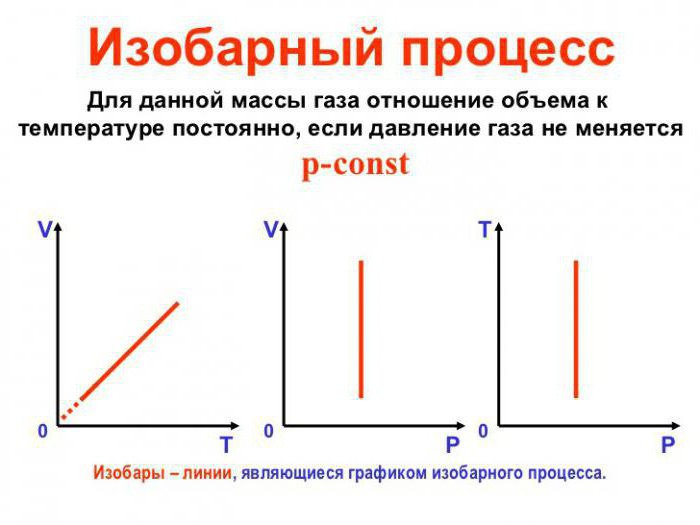
Изобарни процес се може сматрати реверзибилним ако се притисак у систему подудара са спољним притиском и једнак је у свим тачкама процеса (тј. Константан је у вредности), а температура се веома споро мења. Дакле, термодинамичка равнотежа у систему се одржава у сваком тренутку времена. Комбинација горе наведених фактора нам даје могућност да изобарни процес сматрамо реверзибилним.

Да би се извршио изобарични процес у систему, топлота мора бити или испоручена или уклоњена. Истовремено, топлота се мора трошити на рад на ширењу идеалног гаса и његовој промјени. унутрашња енергија. Формула која показује зависност количина једни од других током изобарног процеса назива се Гаи-Луссацовим законом. Показује да је запремина пропорционална температури. Изведимо ову формулу на основу површног знања.

Закључак Гаи-Луссац Закона (примарно разумијевање)

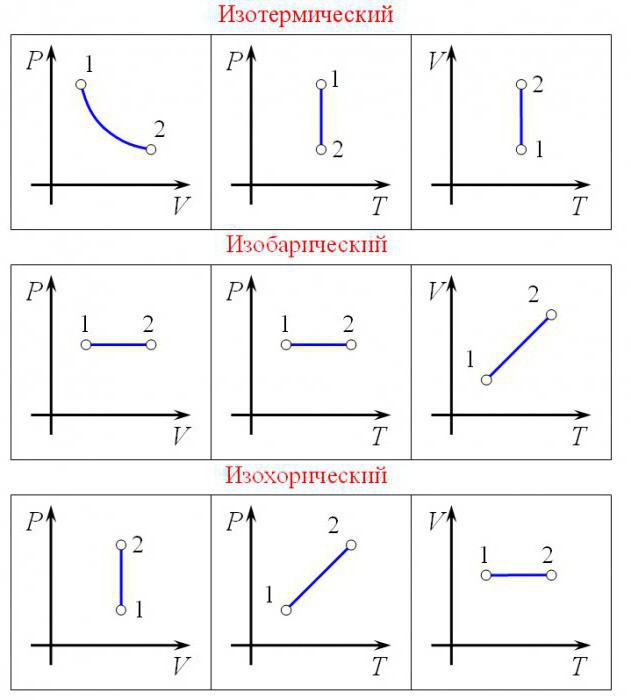
Човек, бар мало упућен у молекуларну физику, зна да су многи задаци повезани са одређеним параметрима. Њихово име је притисак гаса, запремина гаса и температура гаса. У неким случајевима, молекуларна и моларна маса количину супстанце, универзалну гасну константу и друге индикаторе. И постоји одређена веза. Разговарајмо о универзалној гасној константи детаљније. У случају да неко не зна како да га добије.

Добијање универзалне гасне константе

Ова константа (константни број са одређеном димензијом) се такође назива Мендељејева константа. Такође је присутан у Менделејев-Цлапеирон-овој једначини за идеалан гас. Како је наш познати физичар добио ову константу?

Као што знамо, једначина идеалног гаса има следећу форму: ПВ / Т (која је звучала овако: "производ притиска и запремине подељен са температуром"). У односу на универзалну гасну константу, тзв Авогадров закон. Каже се да ако узмемо било какав гас, онда ће једнак број молова на истој температури и истом притиску заузети исту запремину.

У ствари, ово је вербална формулација једначине стања идеалног гаса, која је нешто раније написана у формули формуле. Ако узмемо нормалне услове (а то је када је температура гаса 273,15 Келвина, притисак је 1 атмосфера, односно 101325 Паскала, а волумен мола гаса је 22,4 литара) и ми их замењујемо у једначину, множимо и делимо све, онда добијамо. да нам комбинација таквих акција даје бројчану цифру једнаку 8,31. Димензија је дата у џулима, подељена производом мола до Келвина (ј / мол * к).

Мендељејев-Цлапеирон-ова једначина

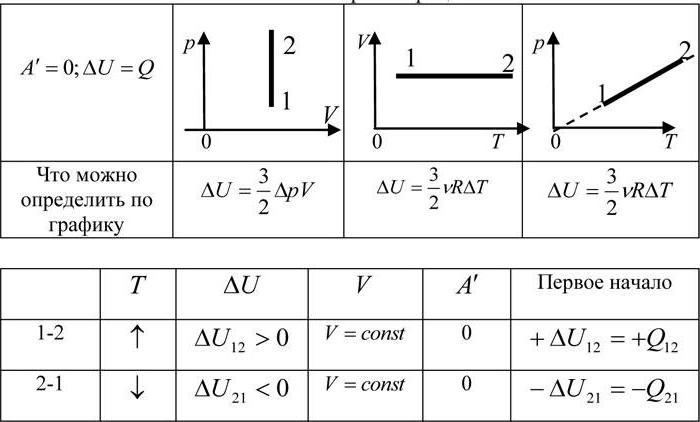
Узмимо једначину стања идеалног гаса и препишемо је у новом облику. Првобитна једначина, подсећамо, има облик ПВ / Т = Р. И сада помножимо оба дела са температурним индексом. Добијамо формулу ПВ (м) = РТ. То јест, производ притиска по запремини једнак је производу универзалне гасне константе по температури.

Сада помножите обе стране једначине са једним или другим бројем молова. Њихов број означавамо словом, рецимо, Кс. Тако добијамо следећу формулу: ПВ (м) Кс = КСРТ. Али знамо да производ В са "м" индексом даје само волумен В, а број мола Кс се открива у облику дељења одређене масе на моларну масу, тј. Она има облик м / М. т

Дакле, коначна формула ће изгледати овако: ПВ = МРТ / м. То је сама једнаџба Мендељејев-Клаперон, којој су оба физичара дошла готово истовремено. Можемо помножити десну страну једначине (и истовремено поделити) за Авогадро број. Тада добијамо: ПВ = КСН (а) РТ / Н (а). Али производ броја молова Авогадровим бројем, тј. КСН (а), не даје нам ништа више од укупног броја молекула гаса, означених словом Н.

Истовремено, квоцијент универзалне гасне константе и Авогадровог броја - Р / Н (а) ће дати Болцманову константу (означену са к). Као резултат, добијамо другу формулу, али у нешто другачијој форми. Ево га: ПВ = НкТ. Можете отворити ову формулу и добити следећи резултат: НкТ / В = П.

Гасни рад у изобарном процесу

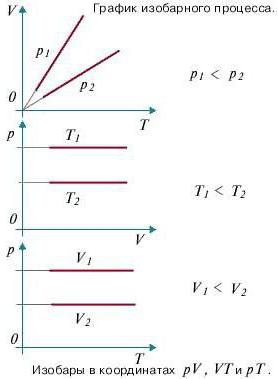
Као што смо раније сазнали, изобарни процес је термодинамички процес у којем притисак остаје константан. А да бисмо сазнали како ће се рад одредити током изобарног процеса, мораћемо да се окренемо првом закону термодинамике. Општа формула је следећа: дК = дУ + дА, где је дК количина топлоте, дУ је промена у унутрашњој енергији, а дА је рад који се обавља током извођења термодинамичког процеса.

Сада посебно размотрите изобарни процес. Узмите у обзир фактор да притисак остаје константан. Сада покушајте да препишете први почетак термодинамике за изобарични процес: дК = дУ + пдВ. Да бисте добили визуелни приказ процеса и рада, морате га приказати у координатном систему. Нека оса апсцисе буде п, ордината оса В. Нека се запремина повећа. На две тачке које се разликују једна од друге са одговарајућом вредношћу п (наравно, фиксне), забележите стања која представљају В1 (почетна запремина) и В2 (коначна запремина). У овом случају, граф ће бити равна линија паралелна са к-осом.

Проналажење посла је лакше него икад. То ће једноставно бити површина фигуре, омеђена с обје стране пројекцијама на оси апсцисе, а на трећој страни правац који повезује тачке које леже на почетку и на крају изобаричне праве линије. Покушајмо да израчунамо вредност рада користећи интегрални.

Израчунаће се на следећи начин: А = п (интеграл између В1 и В2) дВ. Отворимо интеграл. Добијамо да ће рад бити једнак производу притиска на разлику у запреминама. То јест, формула ће изгледати овако: А = п (В2 - В1). Ако откријемо неке количине, добијемо другу формулу. Изгледа овако: А = кР (Т2 - Т2), гдје је к количина твари.

Универзална гасна константа и њено значење

Може се рећи да ће последњи израз одредити физичко значење Р - универзалне гасне константе. Да би било јасније, окренимо се одређеним бројевима. Узмите за тестирање један мол супстанце. Истовремено, нека температура буде 1 Келвин. У овом случају, лако је видети да ће рад гаса бити једнак универзалној гасној константи (или обрнуто).

Закључак

Ову чињеницу можемо приказати у нешто другачијој свјетлости, парафразирајући текст. На пример, универзална гасна константа биће нумерички једнака раду изведеном током изобарног ширења са једним молом идеалног гаса ако се загрева за један Келвин. Нешто ће бити теже израчунати рад са другим изопроцесима, али најважније је примијенити логику. Онда ће све брзо пасти на своје место, а извођење формуле ће бити лакше него што мислите.