Папер флекагон. Како направити узбудљиву слагалицу?

Забавна геометријска папирна играчка која се састоји од неколико троуглова и мења облик када се савије назива флекагон. Од детињства, многи људи се сећају "пребројавања" која је начињена од уобичајеног биљежничког листа. Ако померате прсте са прстима док држите играчку, можете прочитати унапред написане натписе на површинама за отварање. Такав оригами хак је најједноставнији аналог Флекагагона.

Одакле је дошла слагалица?

1930-их, млади Енглез, Артхур Стоне, студирао је Принцетон Университи. У то време, амерички листови папира нису били сасвим стандардне величине - били су краћи за 1,8 цм, а Артхур је морао да пресече папире за нови формат, због чега је случајно почео да скида фигурице из непотребних комада.

Склопио је траку на три мјеста тако да је добио једнакостраничан шестерокут. На крајевима је исекао облик ивица. Када је Артхур залио ивице траке, добио је фасцинантну фигуру. Може се отворити као цветни пупољак, ако један од углова преклопите у центар. И после сваког откривања, појавило се шест нових троуглова.

Овако је измишљен случајно флекацон. Како направити занимљиву загонетку узбудљивијом? Сваку страну можете обојити жељеном бојом, а затим са сваким открићем слика ће имати једну од три боје.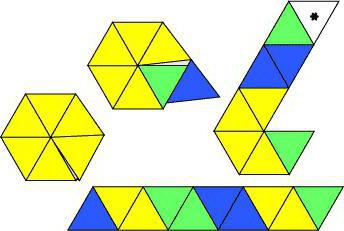

Идеа девелопмент

Стоун захотел сложить многоуровневый шестиугольный флексагон . Артхур Стоне је желио положити шестерокутни флексагон на више разина . Како то урадити, схватио је студент сљедећег јутра. Артхур је саставио фигуру у којој се измјењују 6 различитих површина. Затим, схвативши да постоји математичка теорија која вам омогућава да направите занимљиве шестерокуте, младић је поделио свој рад са пријатељима.

Тьюки , а также Брайан Таккерман . Успут, његови пријатељи су били прави генији егзактних наука: Феинман Рицхард, Јохн Тукеи и Бриан Таккерман . Често су се окупљали у трпезарији и показивали једни другима измишљене загонетке. Стоуном фигуре - флексагон . Била је то пријатељска компанија која је дала име фигурици коју је измислио Стоне - флекагон .

flex ", что значит "сгибать". Она долази од енглеске речи " флек ", што значи "савијати се". Флексагонным комитетом» и даже приступила к написанию математических основ новой науки " флексологии ". Учено тројство се у шали називало " Флекагонов комитет" и чак је почело да пише математичке темеље нове науке о флексологији .

До 40-их година 20. века, Тукеи и Феинман развили су теорију према којој је могуће конструисати флексагон са апсолутним бројем површина и страна. Такође су нацртали све могуће начине да то ураде.

Шта направити флексагон

флексагон . Најчешћи је папирни флексон . Како да га учини трајнијим, није морало дуго размишљати. Облик може бити од дебелог папира или картона. Само линије пресавијања морају бити пажљиво окренуте у оба смјера како би се олакшало додатно склапање облика.

Друга могућност је да флексагон направите издржљивијим - користите подлогу од тканине. Троуглови од папира или картона морају се залијепити на траку тканине, остављајући око 1 мм на линији преклопа. Ова загонетка је поузданија и изгледа оригинално.

Такви различити флексагони

унагексафлексагон . Најједноставнија опција је унагефлекагон . Састоји се од 3 троугла, састављена у траку. Крај је увучен и повезан са другим. всего одну поверхность. Таква фигура се не савија и има само једну површину.

- это бумажный врезанный шестиугольник. Дуогесафлекагон је папирни уграђени шестерокут. Има две стране, али се не савија. тригексафлексагон . Трака од 10 једнакостраничних троуглова састоји се од трихексафлекагонета . Ова фигура већ може да се савија и има три различите површине.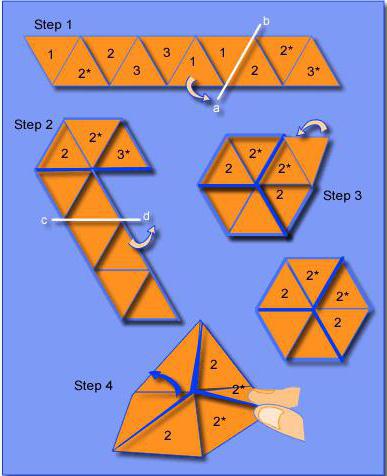

имеет четыре поверхности и складывается из зигзагообразной полоски. Тетрахексафлекагон има четири површине и састоји се од цик-цак траке. пентагексафлексагон обладает пятью поверхностями. По аналогији са претходном сликом, пентахексафлекагон има пет површина.

можно сложить из 19-ти треугольников, собранных в полоску. Хексахексафлекагон се може пресавити из 19 троуглова састављених у траку. Таква фигура има 6 страна. гексагексафлексагона , они собираются из полос сложной формы. Постоје још два типа хексхексафлекагона , који се састављају из трака сложеног облика.

флексагоны сложно, ведь если ошибиться, головоломка будет "заедать". Тешко је саставити и залијепити такве флексагоне , јер ако направите грешку, загонетка ће се "заглавити". включает в себя семь поверхностей. Хептахексафлекагон укључује седам површина. Може се склопити на три различита начина од сложених папирних трака.

Скуаре флекагон

флексагона - это тетрафлексагон . Постоји још један тип флекакагон - тетрафлекагон . Судећи по имену, њихова лица су квадратна, а не трокутаста. Постоје три врсте таквих слагалица:

• ; тритетра флекагон ;
• ; тетратетрафлекагонс ;
• . хекате тетрафлекагон .

тритетрафлексагон , он имеет 3 стороны и складывается из зигзагообразной полосы. Најједноставнији од њих је тритетрафлекагон , има 3 стране и састоји се од цик-цак траке. Према овој шеми, они и даље раде окретни спојеви. У многим дечијим играчкама овај дизајн се користи.

имеют 4 поверхности. Тетратетрофлекагонс има 4 површине. На принципу такве везе, склопиви играчке раде са којима можете показати трикове са нестанком предмета, као што су рачуни.

обладает пятью поверхностями. Хекатетрафлекагон има пет површина. Таква фигура има препознатљиву особину - може се савити дуж хоризонталне и вертикалне оси. складывается из полоски в виде квадратной рамки. Хексатетрофлекагон се састоји од траке у облику квадратног оквира.

Прављење фигуре од 10 троуглова

флексагон из 10 треугольников. Размислите како да направите флексагон од 10 троуглова. тригексафлексагон , а не флексагон . Тачније, добит ћете трихексафлекагон , а не флеклекагон . Како направити корак по корак помоћи ће вам да одредите дијаграм испод.

Прво, исписујемо на листу празно од троуглова. Ако желите, можете нацртати властите трокуте и боје. Затим одсеците траку и савијте крајеве, као што је приказано на сл. 4. Затим савијамо троуглове, формирајући шестерокут. На крају (сл. 8) потребно је залијепити преостали трокут. флексагон из бумаги. Сада знате како да направите флексакагон од папира.

тригексафлексагона необходимо одной рукой ухватить за 2 соседних треугольника, а другой рукой потянуть два противоположных треугольника за их свободные края. Да би се отворио трихексафлекагон потребно је једном руком ухватити 2 сусједна трокута, а другом руком повући два супротна трокута слободним рубовима. Са таквим отвором, шестерокут се окреће на супротној страни, а површина која се претходно скривала излази. Да би било занимљивије открити слику, њене површине морају бити обојене у различитим бојама.