Парадок Монти Халл. Најмање нетачна математика

Теорија вероватноће је грана математике која је спремна да збуни саме математичаре. За разлику од осталих, егзактних и непоколебљивих догми ове науке, ова област обилује необичностима и нетачностима. У овом одељку је недавно додан нови параграф - парадокс Монти Халл-а. То је, у принципу, задатак, али се рјешава на потпуно другачији начин од оних на које смо навикли.

Историја порекла

У парадоксу Монти Халл-а, људи су разбијали главе још од далеке 1975. године. Али вреди почети од 1963. Тада је изашла ТВ емисија под називом Лет'с маке а деал, што се преводи као "Хајде да се договоримо". Његово водјство није било ништа друго него Монти Халл, који је гледаоце каткад бацао на загонетке. Једно од најупечатљивијих је оно које је представио 1975. године. Задатак је постао део математичке теорије вероватноће и парадокса који се уклапају у његов оквир. Такође је важно напоменути да је овај феномен довео до јаких дискусија и оштрих критика од стране научника. Парадокс Монтија Хола објављен је у магазину Параде 1990. године и од тада је постао још дебатиранија и контроверзнија тема свих времена и народа. Па, сада пређите директно на његову формулацију и тумачење.

Формулација проблема

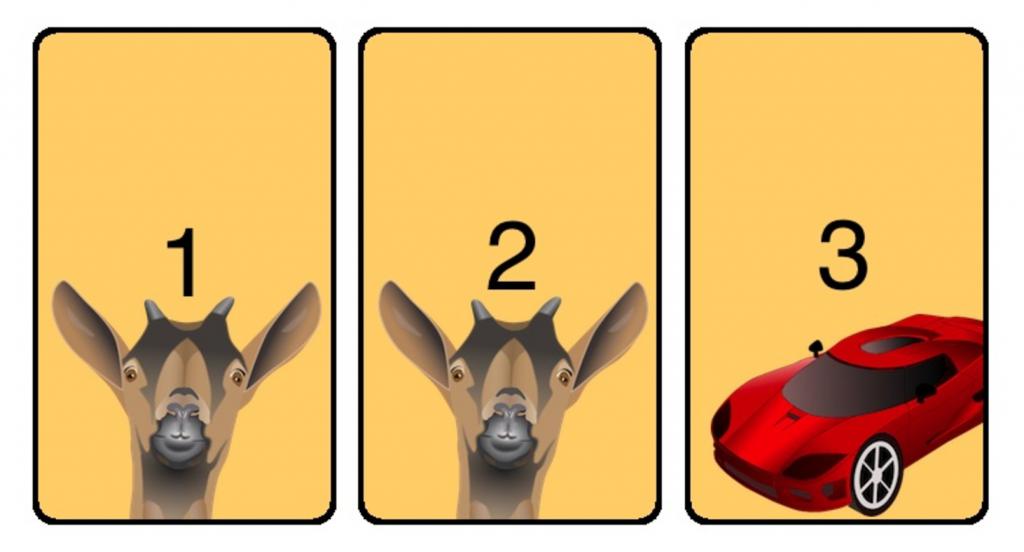
Постоји много интерпретација овог парадокса, али смо одлучили да вам представимо класик, који је приказан у самом програму. Дакле, пре него што су три врата. Иза једне од њих је аутомобил, иза два друга на једној кози. Водитељ вас позива да изаберете једно од врата, и, рецимо, останете на броју 1. До сада не знате шта се налази иза ових првих врата, пошто сте отворили трећи, и показали да иза њега стоји коза. Дакле, још нисте изгубили, јер нисте изабрали врата која скривају опцију губитка. Према томе, ваше шансе за добивање аутомобила се повећавају.

Али овде вам вођа нуди да промените одлуку. Пре него што имате два врата, за једну козу, за још једну жељену награду. То је суштина проблема. Чини се да шансе су 50 до 50. У ствари, ако промените одлуку, вероватноћа да ћете победити ће бити већа. Како то?

Објашњење парадокса Монти Халл-а

Први избор који направите у овој игри је случајан. Не можете чак ни да погодите која је од три врата скривена награда, тако да насумице указује на прву. Вођа, пак, зна гдје су ствари. Има врата са наградом, врата која сте назначили и трећа без награде, коју вам отвара као први траг. Други наговештај лежи у његовом предлогу да промени избор.

Сада нећете изабрати случајно једну од три, али можете чак и промијенити своју одлуку да добијете жељену награду. То је предност која даје особи увјерење да ауто заправо није иза врата која је изабрао, него иза других. То је цела суштина парадокса, јер је, у ствари, потребно изабрати (барем од два, а не од три) насумце, али шансе за победу се повећавају. Како статистике показују, од 30 играча који су се предомислили, освојили су аутомобил 18. А то је 60%. И од тих 30 људи који нису променили одлуку - само 11, то је 36%.

Третман бројевима

Сада дајемо Монти Халл-у парадокс прецизнију дефиницију. Први избор играча разбија врата у две групе. Вјероватноћа да се награда налази иза врата које сте одабрали је 1/3, а иза оних врата која остају 2/3. Водитељ даље отвара једно од врата друге групе. Тако он преноси преосталу вероватноћу, 2/3, на једна врата која нисте изабрали и које он није отворио. Логично је да ће након таквих калкулација бити исплативије промијенити вашу одлуку. Али важно је запамтити да још увек постоји шанса да се изгуби. Понекад водећа лукавост, јер у почетку можете пробити исправна, наградна врата, а након тога добровољно одбити.

Сви смо навикли на чињеницу да математика, као егзактна наука, иде руку под руку са здравим разумом. Овде се ради о бројевима који то чине, а не о речима, тачним формулама, не нејасним рефлексијама, координатама, а не релативним подацима. Али њен нови одељак под називом теорија вероватноће је експлодирао читав познати образац. Задаци из ове области, чини нам се, не улажу у оквире здравог разума и потпуно протурјече свим формулама и калкулацијама. Предлажемо да се упознају са другим парадоксима теорије вероватноће, који имају нешто заједничко са оним који је горе описан.

Парадокс дечака и девојчице

Проблем је, на први поглед, апсурдан, али се строго држи математичке формуле и има два могућа решења. Дакле, одређени мушкарац има двоје дјеце. Један од њих је вероватно дечак. Која је вероватноћа да ће дечак бити други?

Опција 1. Размотрићемо све комбинације двоје деце у породици:

• Девојка / девојка
• Девојка / дечак
• Дечак / девојчица
• Дечак / дечак

Прва комбинација нам очигледно не одговара, дакле, на основу последње три, добијамо вероватноћу 1/3 да ће друго дете бити мали човек.

Опција 2. Ако замислимо такав случај у пракси, одбацујући фракције и формуле, онда, на основу чињенице да на Земљи постоје само два пола, вероватноћа да ће друго дете бити дечак је 1/2.

Парадокс успаване лепотице

Ово искуство нам показује како се може добро манипулирати статистиком. Дакле, успавана лепотица се убризгава таблетом за спавање и баца се новчић. Ако орао падне, онда се пробуди и експеримент престаје. Ако репови испадну, онда је пробуде, одмах направе другу ињекцију, а она заборави да се пробудила, а након тога се поново пробуди само другог дана. Након потпуног буђења "лепоте", непознато је који дан је отворила очи, или каква је вероватноћа да је новчић пао као реп. Према првој варијанти решења, вероватноћа добијања репа (орла) је 1/2. Суштина друге опције је да, ако експеримент проводите 1000 пута, онда у случају орла, "лепота" ће се пробудити 500 пута, а са ретком - 1000. Сада је вероватноћа репа 2/3.