Парадок Зеноа Елеа - опис, значење и занимљивости

Парадокси Зеноа били су збуњени многим научницима и филозофима све до 17. века. И до сада, многи научници расправљају о бесконачности, о структури простора и времена, иако је све почело са неколико парадоксалних изјава које су у први мах поставиле логичну слијепу улицу било које интелигентне особе.

Историја Зенонових парадокса

Зенон Елеа - филозоф античке Грчке, ученик оснивача Елеатичке школе - Парменидес. Живео је од 515. до 450. године пре не, о његовом животу се зна врло мало. Рођен је у граду Елее у јужној Италији. Према Платону, Зено је посетио Атину и срео Сократа. Био је познат по својој апорији, у којој је формулисан чувени Зеноов парадокс. Женске апорије су парадоксално резоновање, сама реч "апорија" из грчког значи "безнађе".

У древна времена, савременици су бројали 40 парадоксалних изјава, а до данас је сачувано само 9, од којих су најпознатије - 4. Зенове апорије научене кроз дјела Аристотела, као и од филозофа као што су Диоген из Лаерта, Платон, Пхилопон, Симплициус. Иначе, вреди споменути саму школу Елеа, којој је припадао Зено. Његова главна учења кажу да је свака промена илузија, биће једно и не мења се. Зено је рекао да је истинска стварност вечна и непроменљива, и може се схватити само уз помоћ разума и логике. Према томе, многи од Зенових апорија посвећени су покрету, у којем он показује да кретање (или промена), са становишта логике, не постоји.

Парадокси о кретању и времену

"Такмичење Ахила и корњача" - један од најпознатијих парадокса Зеноа. Вероватно га сваки школарац познаје. Такодје постоји таква апорија из Зеноа као "Летеце Стрелице", "Дихотомија" и друге. Посвећени су покрету, дискутовани и проучавани два миленијума. Многе студије су биле посвећене њима, а до 17. века, мислиоци нису могли да побијају ову генијалну логику.

Проблем је ријешен након идеје диференцијалног рачунања, коју су предложили Невтон и Леибниз. Постоји појам "граница", тако да је разлика између времена раздвајања и раздвајања одређеног пута на сегменте постала јасна. Поред тога, мистерија је решена када су научници научили да користе бесконачно мале количине. Женска апорија је од тада произвела много различитих варијација. Осим тога, можда су додали неке детаље. Навешћемо парадоксе Зеноа који су преживели до данас и укратко описујемо њихову суштину. У сваком случају, покушајте то учинити.

Зеноов парадокс Ахила и корњача

Јунак митова античке Грчке, Ахил, такмичи се у брзини са корњачом. Услови су такви да корњача креће мало даље, Ахил је удаљен 1000 корака од њега.

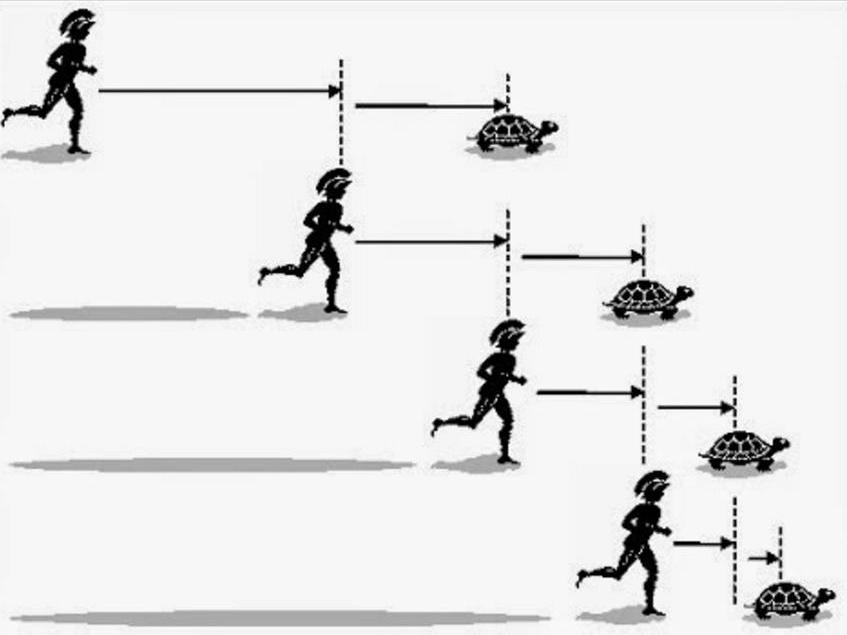
Да би сустигао корњачу, Ахил мора прво стићи до места одакле је корњача почела. Али чим стигне до тог места, корњача ће имати времена да прође 100 корака. Ова удаљеност, коју је пузала, тек треба да надвлада Ахил, али до тог тренутка она ће пузати 10 корака даље и тако даље. Број таквих сегмената које Ахил треба да превазиђе, према Зену, може бити бесконачан, јер ће величина ових сегмената све време бити сведена на бесконачно мале вредности.

Испоставља се да ако следите ту логику, антички грчки јунак никада неће достићи корњачу. Парадокс Зеноа је постојање бесконачног броја бесконачно малих сегмената, али у стварном животу тркач ће сигурно престићи животињу која се споро креће.

Флиинг арров

Овај парадокс се зове Арров. Ово је још једна апорија коју је Зено формулисао приближно следећим речима. Ако се нешто покреће, онда се креће или на мјесту које заузима, или се креће тамо гдје не постоји. Али не може да се креће на месту које заузима. Пошто у свакој секунди заузима цело место. Али тамо где није, не може се померити. Дакле, сам покрет је немогућ.

Према Зену, стрелица, када лети, истовремено је у мировању. Зато што у сваком тренутку заузима исти простор, једнак њему. То јест, стрелица остаје у мировању у односу на мјесто гдје се налази у одређеном временском периоду. Испоставља се да је летећа стрела непомична. Ако је у одређеном тренутку непомична, то значи да је у мировању иу другим временима. И нема тренутка када се стрела померила.

Дицхотоми

Парадокс, који ће бити дат у наставку, назива се "дихотомија". Преведено са грчког језика, то значи "раздвојити се на два", а дао га је Аристотел. Ова апорија је постављена приближно на исти начин као и Зеноов парадокс Ахила и корњаче.

Оригинал говори о тркачу, који није у стању ни да почне, јер покрет, према Зену, не постоји. Али постоји и уобичајена могућност преласка собе.

Да бисте прешли собу, прво морате да пређете пола собе. Требат ће одређена јединица времена. Након тога, одређена дистанца ће остати, морате превазићи половину тога за још једну јединицу времена. Тада је остао преостали дио пута који се у исто вријеме дијели на двије и пол овог сегмента. Онда опет постоји одређена удаљеност, од које се половина мора прећи. Испоставља се да се соба може прећи на неодређено време.

Две колоне на стадиону

Две колоне људи, исте дужине, које се крећу паралелно са истом брзином у супротним правцима. Према Зену, време које истиче када колоне пролазе једна поред друге је једнако половини времена које једна особа треба да прође кроз целу колону.

Резолуција Зенонових парадокса

Од четири горе наведене апорије, прве три су биле најпознатије. Четврта се појавила због погрешног разумијевања природе релативног кретања.

Све апорије се лако могу оповргнути експериментално. Ништа не спречава прелазак собе, отпусти стрелицу и престићи корњачу.

Узмите у обзир парадокс повезан са преласком из једне собе. Наравно, ако поделите раздаљину на пола и одете на пола, биће потребно одређено време. И даље ће постојати дистанца, коју такође треба поделити у две и по. Али за ово време биће потребно пола времена. Што је мања удаљеност коју треба покрити, то ће се више смањити вријеме за њен пролаз. Испоставља се да када прелазите собу на крају, потребан је неограничен број бесконачно малих временских периода. Али ако збројите све сегменте, добићете одређени број - то ће бити време које сте провели прелазећи собу. Испоставило се да је сасвим могуће прећи собу за одређени временски период. Овај доказ је сличан налазу границе у диференцијалном рачуну. Древни грчки филозоф Зенон погрешно претпоставио је да пролазак бесконачно малих удаљености захтијева исто вријеме сваки пут.

Што се тиче Зеноновог парадокса, "Летећа стрелица", Аристотел га је критиковао тврдећи да сваки тренутак времена не може бити недељив сам по себи. Рекао је и да је Зеноово образложење да ако све што заузима једнако мјесто остаје у мировању, и ако оно што је у покрету увијек заузима исто мјесто у било којем тренутку, онда је стрелица непомична, погрешна.

Куантум еффецт

Парадокси Зеноа су с временом оповргнути многи научници. Али они су и даље доприносили науци. У квантној физици тренутно постоји нешто као што је квантни парадокс Зеноа. Она лежи у чињеници да, ако посматрате нестабилну честицу, на пример, да мерите, проверите да ли је нека честица пропала или не, онда постоји неко успоравање у радиоактивном распаду.

Претпоставља се да ако непрестано посматрате честицу, она се можда неће уопште распасти. Деведесетих година прошлог века овај квантни ефекат је потврђен низом експеримената.