Период осцилација: експерименти, формуле, задаци

Који је период осцилације? Каква је то вредност, какав физички смисао има и како је израчунати? У овом чланку ћемо се позабавити овим питањима, размотрити различите формуле помоћу којих можете израчунати период осцилација, као и сазнати који однос постоји између физичких величина као периода и фреквенције осцилације тијела / система.

Дефиниција и физичко значење

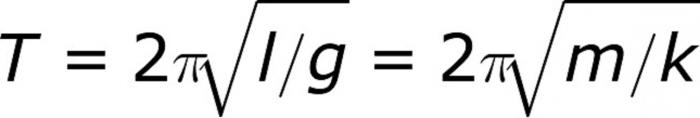
Период осцилације назива се период у којем тијело или систем обавља једну осцилацију (нужно комплетну). Паралелно, могуће је уочити параметар код којег се осцилација може сматрати комплетном. Улога таквог стања је повратак тела у првобитно стање (на оригиналну координату). Веома добра аналогија са периодом функције. Погрешно је, узгред речено, мислити да се одвија искључиво у обичној и вишој математици. Као што знате, ове две науке су нераскидиво повезане. И период функција се може сусрести не само при рјешавању тригонометријских једнаџби, већ иу различитим секције физике, наиме, говоримо о механици, оптици и другима. Приликом преношења периода осцилација из математике у физику, потребно је разумјети само физичку величину (а не функцију), која је директно овисна о времену проласка.

Које су флуктуације?

Осцилације су подељене на хармонијске и анхармоничне, као и периодичне и непериодичне. Било би логично претпоставити да се у случају хармонијских осцилација изводе према некој хармонијској функцији. Може бити и синус и косинус. У овом случају, могу постојати коефицијенти растезања и повећања-смањивања. Такође, осцилације су пригушене. То јест, када одређена сила делује на систем, који постепено “успорава” саме осцилације. Истовремено, период постаје мањи, док је фреквенција осцилација у сталном порасту. Веома добро демонстрира тако једноставан аксиом физичког искуства са употребом клатна. Може бити прољетног типа, као и математички. Није важно. Иначе, период осцилација у таквим системима ће бити одређен различитим формулама. Али о томе касније. Сада дајемо примере.

Искуство са клатном

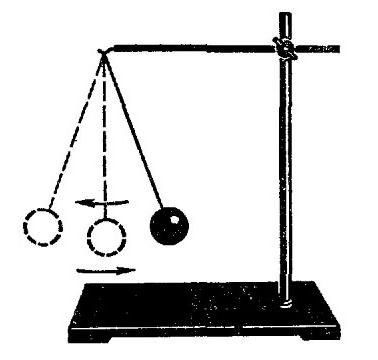
Било које клатно се може узети прво, неће бити разлике. Закони физике и закони физике, који се у сваком случају поштују. Али из неког разлога више наликује математичком клатну. Ако неко не зна шта је: ово је лопта на нерастављивој нити која је причвршћена на хоризонталну шипку причвршћену за ноге (или елементе који играју своју улогу - да одрже систем у равнотежи). Лопта је најбоље узети из метала, тако да је искуство било јасније.

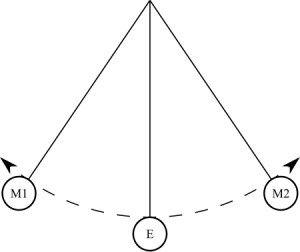
Дакле, ако извучете такав систем из равнотеже, примените неку силу на лопту (другим речима, гурните је), онда ће лопта почети да се љуља по нити, пратећи одређену путању. Временом ћете приметити да се путања кроз коју пролази лопта смањује. Истовремено, лопта почиње да се креће напред и назад све брже и брже. То сугерише фреквенција осцилација повећава. Али време за које се лопта враћа у почетни положај се смањује. Али време једног потпуног осциловања, како смо раније сазнали, назива се период. Ако се једна вредност смањи, а друга повећа, онда говоримо о обрнутој пропорционалности. Тако смо дошли до прве тачке, на основу које су изграђене формуле за одређивање периода осцилација. Ако узмемо клатно за пролеће, онда ће се закон тамо посматрати у нешто другачијој форми. Да бисмо га најјасније представили, систем ћемо покренути у вертикалној равни. Да би било јасније, испрва је вредело рећи шта је пролећни њихало. Из назива је јасно да у његовом дизајну мора бити присутан извор. И то је истина. Поново имамо хоризонталну раван на носачима, на коју је обустављена опруга одређене дужине и крутости. За њу је заузврат суспендована тежина. Може бити цилиндар, коцка или друга фигура. Можда је чак и нека ставка треће стране. У сваком случају, приликом уклањања система из равнотежног положаја, он ће почети да производи пригушене осцилације. Најјасније видљиво повећање фреквенције је у вертикалној равни, без икаквих одступања. Са овим експериментима можете завршити.

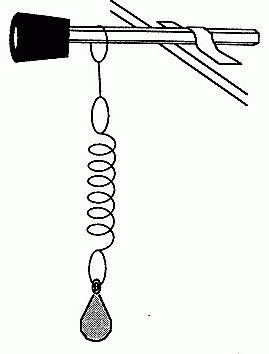
Дакле, у њиховом току смо открили да су период и фреквенција осцилација две физичке величине које имају инверзни однос.

Означавање количина и димензија

Обично је период осцилације означен латиничним словом Т. Много рјеђе се може означити другачије. Фреквенција је означена словом µ ("Му"). Као што смо рекли на самом почетку, период није ништа више од времена када се у систему јавља потпуна осцилација. Тада ће димензија периода бити друга. Пошто су период и фреквенција обрнуто пропорционални, онда ће димензија фреквенције бити подељена са другом. У снимању задатака, све ће изгледати овако: Т (с), µ (1 / с).

Формула за математички клатно. Проблем број 1

Као иу случају експеримената, одлучио сам прво да се бавим математичким клатном. Нећемо детаљно улазити у извођење формуле, јер такав задатак није био постављен у почетку. И сам закључак је гломазан. Али, хајде да погледамо саме формуле, да сазнамо које су вредности у њима. Дакле, формула за период осцилације математичког клатна је следећа:

Где л - дужина конца, н = 3.14, и г - убрзање фрее фалл (9.8 м / с ^ 2). Формула не би требало да изазива никакве потешкоће. Стога, без додатних питања, одмах прелазимо на решавање проблема одређивања периода осцилација математичког клатна. Метална кугла тежине 10 грама је обешена на нерастављиву нит дугу 20 центиметара. Израчунајте период осцилације система, узимајући га као математички клатно. Решење је веома једноставно. Као иу свим физичким проблемима, потребно је што више га поједноставити због одбацивања непотребних ријечи. Они су укључени у контекст како би се збунили они који одлучују, али заправо немају никакву тежину. У већини случајева, наравно. Овде можете да искључите тренутак са “неразложивом нити”. Ова фраза не би требало да улази у ступор. А пошто имамо математички клатно, не бисмо требали бити заинтересовани за масу терета. То значи да речи око 10 грама такође једноставно замењују ученика. Али знамо да у формули нема масе, тако да са чистом савешћу можемо да наставимо са доношењем одлуке. Дакле, узимамо формулу и једноставно замењујемо њене вредности, јер је потребно одредити период система. Пошто нису наведени никакви додатни услови, заокружићемо вредности на трећу децималу, као што је уобичајено. Множењем и подјелом вриједности, добијамо да је период осцилације 0,886 секунди. Проблем решен.

Формула за пролећно клатно. Проблем број 2

Формуле клатна имају заједнички део, наиме 2п. Ова вредност је присутна у две формуле одједном, али се разликују у радикалном изразу. Ако се у задатку који се односи на период клатна опруге, укаже на тежину оптерећења, онда је немогуће избјећи рачунање са његовом примјеном, као што је то био случај са математичким клатном. Али не треба се плашити. Ово је формула за период пролећног клатна:

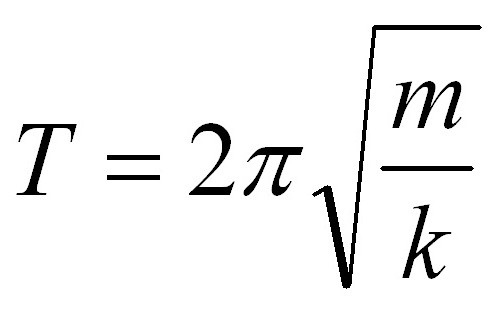
У њој, м је маса оптерећења оптерећеног од опруге, к је константа опруге опруге. У задатку се може дати вриједност коефицијента. Али ако у формули математичког клатна нисте посебно чисти - на крају крајева, 2 од 4 вредности су константе - додаје се 3 параметра, који се могу променити. А на излазу имамо 3 варијабле: период (фреквенција) осцилација, константа опруге опруге, маса висећег терета. Задатак може бити оријентисан на проналажење било којег од ових параметара. Било би сувише лако погледати поново за одређени период, тако да ћемо мало промијенити стање. Нађите коефицијент крутости опруге ако је укупно време осцилација 4 секунде, а тежина оптерећења опруге клатна је 200 грама.

Да би се решио било који физички проблем, било би добро да прво нацртате слику и напишете формуле. Овде су пола битке. Пишући формулу, потребно је изразити коефицијент крутости. Имамо га испод корена, па ћемо изједначити обе стране једначине. Да бисте се ослободили фракције, помножите делове са к. Сада остављамо само коефицијент на левој страни једначине, то јест, делимо делове са Т ^ 2. У принципу, задатак би могао бити мало тежи, не одређивање периода у бројевима, већ учесталост. У сваком случају, приликом рачунања и заокруживања (договорили смо се да се заокружимо на треће децимално место), испада да је к = 0, 157 Н / м.

Период слободних осцилација. Формула времена слободних осцилација

У формули за период слободне вибрације разумети формуле које смо издвојили у два претходно наведена проблема. Једнаџба слободних осцилација је такође компилирана, али ми већ говоримо о померањима и координатама, а ово питање се односи на други чланак.

Савјети за рјешавање проблема везаних за период

1) Пре него што преузмете задатак, запишите формулу која је са њом повезана.

2) Најједноставнији задаци не захтевају слике, али у изнимним случајевима они ће морати да се ураде.

3) Покушајте да се ослободите корена и именитеља, ако је могуће. Једначина написана у реду, без имениоца, много је лакше и лакше решити.