Правокутни трапезоид: све формуле и примјери задатака
Задаци са трапезом не чине се тешким у бројним цифрама које су раније проучаване. Као посебан случај, разматра се правоугаони трапез. А када се тражи његова област, понекад је погодније да се подели на два већ позната: правоугаоник и троугао. Треба само мало помислити, и постоји рјешење.
Дефиниција правоугаоног трапеза и његових својстава
Код произвољног трапеза, базе су паралелне, а стране могу имати произвољну вредност углова према њима. Ако се разматра правоугаони трапез, онда је у њему једна од страна увек окомита на базе. То значи да ће два угла бити једнака 90 степени. Штавише, они увек припадају суседним врховима или, другим речима, једној страни.
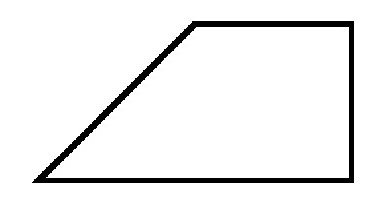
Остали углови у правоугаоном трапезу су увек оштри и тупи. А њихова сума ће увек бити једнака 180 степени.
Свака дијагонала се формира са својом мањом страном правоугаони троугао. А висина, која се извлачи са врха са тупим углом, дели слику на две. Један је правоугаоник, а други је прави троугао. Иначе, ова страна је увек једнака висини трапеза.
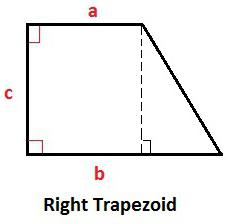
Које ознаке су прихваћене у представљеним формулама?
Све вредности које се користе у различитим изразима које описују трапез, су одмах назначене и приказане у табели:
| Магнитуде | Његова ознака |
| а | већа база |
| б | мања основа правокутног трапеза |
| ц, х | окомито на основну страну, висину |
| д | слопинг сиде |
| α | акутни угао |
| β | туп кут |
| м | трапезна средња линија |
| д 1 | мање дијагонале |
| д 2 | велика дијагонала |
Формуле које описују елементе правоугаоног трапеза
Најједноставнији од њих односи се на висину и мању страну:
ц = х.
Неке формуле за ову страну правокутног трапеза:
ц = д * синα;
ц = (а - б) * тг α;
ц = √ (д2 - (а - б) 2 ).
Први следи из правог троугла. И каже да нога до хипотенузе даје синус супротног угла.
У истом троуглу друга нога је једнака разлици две базе. Стога је истинита тврдња која изједначава тангенс угла са односом ногу.
Из истог троугла може се извести формула заснована на познавању Питагорине теореме. Ово је трећи забележени израз.
Формуле за другу страну могу бити написане. Они су такође три:
д = (а - б) / цосα;
д = ц / син α;
д = √ (ц 2 + (а - б) 2 ).
Прва два се поново добијају из аспекта у истом правоугаоном троуглу, а други је изведен из Питагорина теорема.
Која се формула може користити за израчунавање површине?
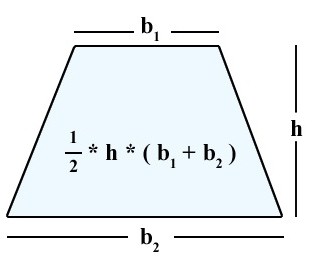
Оно што се даје за произвољни трапез. Само је потребно узети у обзир да је висина страна окомита на базе.
С = (а + б) * х / 2.
Ове вредности нису увек дате експлицитно. Стога, да бисте израчунали површину правокутног трапеза, потребно је извршити неке математичке прорачуне.
Шта ако требате израчунати дијагоналу?
У овом случају, морате да видите да они формирају два правоугаона троугла. Дакле, увек можете користити Питагорину теорему. Тада ће се прва дијагонала изразити као:
д1 = √ (ц 2 + б 2 )
или на други начин, замјењујући "од" са "х":
д1 = √ (х 2 + б 2 ).
Слично томе, добијене су формуле за другу дијагоналу:
д2 = √ (ц 2 + б 2 ) или д 2 = √ (х 2 + а 2 ).
Проблем број 1
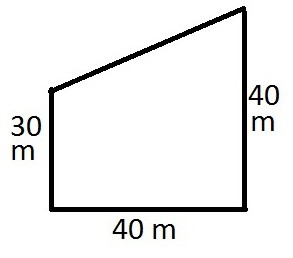
Цондитион Подручје правокутног трапеза је познато и износи 120 дм 2 . Његова висина је 8 дм. Потребно је израчунати све стране трапеза. Додатни услов је да је једна база мања од друге за 6 дм.
Одлука. Пошто је дат правоугаони трапезоид, у коме је висина позната, можемо одмах рећи да је једна страна једнака 8 дм, односно мања страна.
Сада можете рачунати друго: д = √ (са 2 + (а - б) 2 ). И овде су обе стране и разлика у основама одмах дате. Ово последње је 6 дм, то је познато из стања. Тада ће д бити једнако скуаре роот од (64 + 36), то јест, од 100. Тако је пронађена друга страна, једнака 10 дм.
Збир база може се наћи из формуле за подручје. Она ће бити једнака двострукој вредности површине подељене са висином. Ако рачунате, испоставља се да је 240/8, тако да је збир база 30 дм. С друге стране, њихова разлика је 6 дм. Комбинујући ове једначине, можемо рачунати обе базе:
а + б = 30 и а - б = 6.
Можете изразити а као (б + 6), замијенити га у првој једнакости. Тада се испоставља да ће 2б бити једнако 24. Дакле, само б ће бити 12 дм.
Тада је последња страна а једнака 18 дм.
Одговор је. Стране правоугаоног трапеза: а = 18 дм, б = 12 дм, ц = 8 дм, д = 10 дм.
Проблем број 2
Цондитион Дати правокутни трапезоид. Његова велика страна једнака је збиру база. Њена висина је 12 цм, правоугаоник је изграђен, чије су стране једнаке бази трапеза. Потребно је израчунати површину овог правоугаоника.
Одлука. Морате почети са жељеним. Тражена површина се одређује као производ а и б. Обе ове количине нису познате.
Потребно је користити додатне једнакости. Један од њих се заснива на изјави из услова: д = а + б. Потребно је користити трећу формулу за ову страну, која је дата горе. Испада: д 2 = ц 2 + (а - б) 2 или (а + б) 2 = ц 2 + (а - б) 2 .
Потребно је извршити трансформацију, замењујући уместо њене вредности са условом - 12. Након отварања заграда и излагања таквих термина, испада да је 144 = 4 аб.
На почетку одлуке речено је да а * б даје тражену област. Стога, у задњем изразу, овај производ можете замијенити са С. Једноставна калкулација ће дати вриједност подручја. С = 36 цм 2 .
Одговор је. Потребна површина је 36 цм 2 .
Проблем број 3
Цондитион Подручје правокутног трапеза 150√3 цм². Оштар угао је 60 степени. Угао између мале базе и мање дијагонале има исту вриједност. Потребно је израчунати мању дијагоналу.
Одлука. Из својстава трапезоидних углова, испада да је његов тупи угао 120º. Тада га дијагонала дели на једнаку, јер је један њен део већ 60 степени. Тада је угао између ове дијагонале и друге базе такође 60 степени. То јест, троугао који је формиран великом базом, косом страном и мањим дијагоналама, је једнакостран. Тако ће жељена дијагонала бити једнака а, као и страна д = а.
Сада морамо да размотримо прави троугао. У њему, трећи угао је 30 степени. Дакле, нога која лежи на њој једнака је половини хипотенузе. То значи да је мања база трапеза једнака половини жељене дијагонале: б = а / 2. Из њега је потребно пронаћи висину која је једнака бочној, окомитој на базе. Страна са овде је нога. Из Питагорина теорема:
ц = (а / 2) * .3.
Сада остаје само да се све вредности замене у формули:
150√3 = (а + а / 2) * (а / 2 * )3) / 2.
Решавање ове једначине даје корен од 20
Одговор је. Мања дијагонала је 20 цм дуга.