Репулсивна снага: узрок настанка, формула и примјери рјешавања проблема
Плутајући бродови и чамци на морима и океанима, летећи ваздушни бродови и балони, све су то примјери дјеловања такозване силе узгона у текућим супстанцама. Каква је то моћ, одакле долази и како се она може израчунати? Чланак ће одговорити на ова и друга питања.
Хидростатски и аеростатски притисак
Управо ови притисци узрокују силу потискивања која дјелује на тијело у текућим и плиновитим медијима. Ова агрегатна стања материје састоје се од молекула и атома, који се насумично крећу кроз читав волумен супстанце. Као резултат овог покрета, сударајући са чврстим материјама, честице течне материје стварају притисак на њих. Међутим, укупни притисак у било којој елементарној запремини је нула. Пошто су сви правци кретања честица једнаки.
Када се течна супстанца стави у гравитационо поље (привлачност наше планете), онда сваки слој који лежи испод доживљава притисак из горњег слоја, створен тежином потоњег. Овај притисак у течностима назива се хидростатички, ау гасовима аеростатски. Дакле, за течности чија се густина мало разликује од дубине, овај притисак се може израчунати помоћу следеће формуле:
П = ρ л * г * х
Где су х и ρ л дубина и густина течности, респективно. На пример, за воду са повећаном дубином на сваких 10 метара, хидростатски притисак се повећава за једну атмосферу (≈ 10 5 Па).
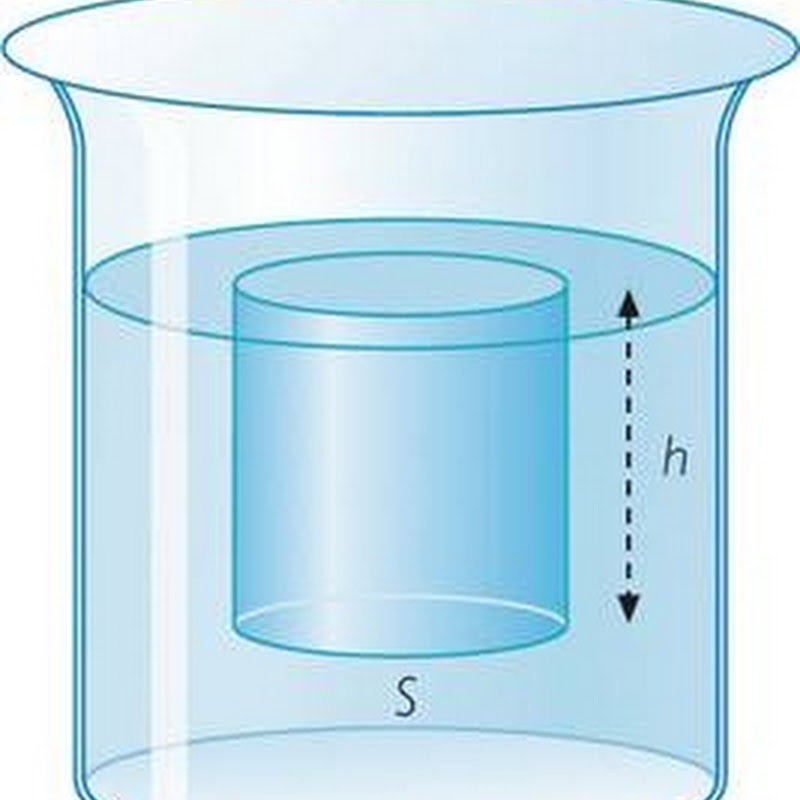
Како хидростатски притисак ствара узгон?
Изнад, нађено је да горњи слојеви притиска флуида на ниже због његове озбиљности. У КСВИИ веку, Блаисе Пасцал, проучавајући понашање течности и гасова, открио је да ако их притиснете, они га једнако преносе у свим правцима. Течности обављају ову трансмисију без губитака због своје некомпресибилности, а гасови - са губитком компресије самог гаса.
Описани Пасцалов закон игра кључну улогу у разумијевању природе појаве силе узгона на тијелу уроњеном у флуидну твар. Претпоставимо да имамо коцку од неког материјала. Ако увучете ову коцку у супстанцу (течност, гас), она ће почети да делује на статички притисак. Он ће деловати на свим странама коцке окомито на њу. Настали вектор притиска на бочним странама ће бити нула. Притисак на горе делује на дно. И на врху - доле. Штавише, први модул ће бити већи од другог, пошто је доња ивица на већој дубини. Користећи формулу за силу кроз притисак можемо да напишемо следећи израз:
Ф = (П 2 - П 1 ) * С = ρ л * г * С * (х 2 - х 1 ) = ρ л * г * В с
Овде је С површина лица, х 2 и х 1 су дубине на којима се налазе доња и горња страна коцке, респективно, В с је запремина коцке. Вредност Ф се назива сила узгона.
Архимедов принцип
Треба напоменути да у формули за Ф добијену у претходном параграфу, производ густине течности и запремина тела одговара маси расељене супстанце. Производ масе и убрзања г је тежина расељене супстанце. Према томе, може се рећи да тело усмјерено вертикално према горе дјелује на тијело потпуно уроњено у флуидну супстанцу, сила према горе Ф, чији је модул једнак тежини расељене твари. Ова формулација се сада зове закон, или Архимедов принцип.
У ИИИ веку пре нове ере, грчки филозоф Архимед, један од краљева предложио је да се проблем ријеши: било је потребно утврдити, без кварења краљевске круне, да је направљен од злата или другог метала. Филозоф је успјешно ријешио овај проблем мјерењем тежине круне у води и зраку, након чега је користио концепт узгона. Из тог разлога, ово друго се зове Архимедов. У ваздуху се назива и лифт.
Зашто се нека тијела спуштају, а друга пливају?

Одговор на ово питање лежи у равнотежи гравитације и Архимедова. Пошто је прва усмерена вертикално надоле, а друга - навише, онда ако сила гравитације премаши Архимедов модул, онда ће тело потонути. Напротив, ако је разлика између модула потисне силе и гравитације позитивна - тијело ће остати на површини флуида или се подићи у зрак.
Добијамо математичку формулацију услова за тела пливања. Да бисмо то урадили, пишемо однос ових сила, користећи формулу за њих:
Ф А > Ф г =>
ρ л * г * В с > ρ с * г * В с =>
ρ л > ρ с
Овде су Ф А и Ф г Архимедова сила и гравитација. Вредност ρ с је просечна густина тела.
Тако ће свако тело остати на површини у флуиду или ће се уздићи у ваздух ако је његова густина мања од густине течне супстанце.
Задатак израчунавања моћи Архимеда
Познато је да је густина ваздуха 1.225 кг / м3 на температури од 15 ° Ц. Знајући да загрејани ваздух у балону има густину од 1 кг / м 3 , потребно је сазнати која плутајућа сила делује на њу. Какво оптерећење може да подигне лопту? Волумен лопте је 3000 м 3 .

Израчунајте две силе: подизање и гравитацију. Имамо:
Ф А = ρ л * г * В с = 1.225 * 9.81 * 3000 = 36052 Н
Ф г = ρ с * г * В с = 1 * 9.81 * 3000 = 29430 Н
Тежина оптерећења П, коју кугла може подићи, једнака је разлици између тих сила. Израчунај:
П = Ф А - Ф г = 36052 - 29430 = 6622 Н
Погодно је да се добијена вредност претвори у масу м. Имамо:
м = П / г = 6622 / 9,81 = 675 кг
Према томе, разматрани балон је у стању да подигне у ваздух 10 људи тежине 67 кг.
Задатак одређивања Архимедове силе у води
Претпоставимо да постоји коцка направљена од неке чврсте материје са густином од 600 кг / м 3 . Дужина њеног руба је 12 цм, а неопходно је одредити силу узгона воде, ако је коцка бачена у њу.

Пошто је густина коцке мања од густине воде, она ће плутати на њеној површини. Будући да је на површини, коцка неће бити потпуно уроњена у воду, па је, да би се израчунала узгонска сила, потребно израчунати запремину воде која се расипа. Ипак, проблем се може ријешити на другачији начин.
Пошто је објекат у равнотежи на површини воде, узгонска сила мора бити једнака сили гравитације. Ово последње се може израчунати множењем густине коцке са његовом запремином. Имамо:
Ф А = Ф г = ρ с * В с * г = ρ с * а 3 * г
Овде а је ивица коцке. Замењујући податке из изјаве проблема, налазимо да ће плутајућа сила која делује на тело бити једнака 10.2 Н.