Школска математика: зашто не поделити на нулу у школи?

Подела са 0 поставља многа питања за оне људе који су се бавили математиком и имали су контакт са њом само у фази школског образовања. У време када дете почиње да проучава операције умножавања и дељења уопште, случај се такође примењује подела на нулу. У овом тренутку, учитељ каже, најчешће, да је немогуће поделити на нулу и ... то је све.

Објашњења у овој фази су завршена. Не можеш, па чак ни прснути

Испред студента постоји дилема - узмите ријеч за наставнике и напишите да нема одговора у примјеру гдје се таква операција појављује или покушајте ријешити ово питање. Али већина родитеља, који су већ давно завршили школу и безбедно су бацили сва знања која су им у школу додељена у школу (осим оних који су им некако били корисни у животу), нису могли много помоћи у томе. . А излаз је релативно једноставан. Па, ако учитељ дође до питања, зашто се не може поделити са нулом, са креативне стране. Да би се то урадило, биће довољно да се обављају нормалне операције са јасном демонстрацијом процеса. О чему се ради?

Демонстрација разних операција подјеле помоћу акција које свака особа може разумјети

Можете узети неколико јабука, на пример, шест комада, и објаснити да је 6 број који треба поделити, односно, према проучаваним математичким терминима, ово је дивиденда. Учитељ стоји поред табле, а испред њега на столу је 6 јабука. Онда он позива двоје људи из класе и дели ове јабуке подједнако између њих. То јест, двоје људи у овом случају се залажу за делиоца - број на који треба поделити дивиденду. Наставник сваком ученику даје три јабуке. То значи да се процес поделе одвија управо онда када је учитељ предао јабуке у руке ученика. И три јабуке у рукама сваког детета - то је квоцијент поделе.

Подела нула бројем - показује порекло процеса

Питање, зашто је немогуће поделити нулу, произлази из обрнуте ситуације - зашто је могуће поделити нулу по броју? Сада смо паметни и знамо да се било који број може поделити на други, и да ће бити потпуно подељен, или ће се појавити фракција, или чак негативни знак, роот или Пи број - све је могуће. Али са нултом загонетком и све то.

Шта се дешава када поделите нулу бројем?

Да бисмо објаснили да је немогуће поделити на нулу, хајде да прво разумемо шта се дешава када се 0 подели одређеним бројем. Исти учитељ стоји поред плоче и нема ништа на столу. Пред њим је празнина, нула. Када ученици дођу код њега и пруже руке да би добили свој приватни, учитељ то са њим дели без ичега, само додирујући њихове дланове. То јест, он је имао једно велико ништа и није дао ништа двоје студената. Тако постаје јасно да се подела нуле било којим бројем одвија, јер је дошло до процеса трансфера. Једина разлика је да са нултим резултатом.

Случај три

Сличну, трећу ситуацију треба извршити како би се показало зашто је немогуће подијелити на нулу. Наставник је у својим рукама или на столу испред њега опет исте те шест јабука као у првој ситуацији. Али поделимо на нулу, јер се нико не приближи јабукама.

То јест, та два студента који су дошли раније у првој ситуацији били су број 2. Да би представили број 0, испоставило се да нико не би требао ићи. Као што се сећамо, прелазак са руку учитеља јабука на руке ученика је процес поделе. Али сада нема ученика, а процес дијељења се не дешава ни са ким. Из овога се испоставља да је немогуће поделити на нулу. За дјецу на нивоу школе ово је основно објашњење.

Једноставно и лако објаснити. И онда нека наставници института учине исто

Већ након уласка у високошколску установу и проучавања концепта границе, на пример, уклања се питање зашто је немогуће поделити на нулу, јер се испоставља да се то може урадити. Раздвајајући нешто од нуле, добијамо бесконачност, неизвесност. 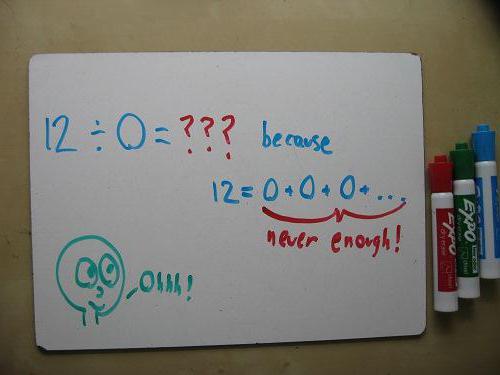Бесконачна димензија таквог резултата још није у потпуности дефинисана, а особа која нема посебно математичко образовање није у стању да схвати зашто је то потребно, који су циљеви остварени у рјешавању ове операције и што она даје. Међутим, за ученике школског узраста, горе описано објашњење је сасвим довољно да задовољи њихову жељу да схвате зашто је још увијек немогуће подијелити се на нулу - не само рећи ово и ставити дјецу пред чињеницу, већ им дати занимљиво и забавно објашњење.