Историја Питагорине теореме. Доказ теореме
Они који су заинтересовани за историју Питагорине теореме, која се проучава у школском курикулуму, такође ће знатижељно знати да ће 1940. године бити објављена књига са три стотине и седамдесет доказа те наизглед једноставне теореме. Али она је интригирала умове многих математичара и филозофа различитих епоха. У Гуиннессовој књизи рекорда, она је фиксирана као теорема са максималним бројем доказа.
Историја Питагорине теореме
Повезан са именом Питагора, теорема је била позната много прије рођења великог филозофа. Тако је у Египту, током изградње структура, узет у обзир омјер правог трокута од прије пет хиљада година. Бабилонски текстови се односе на исти омјер слике. правоугаони троугао 1200 година пре рођења Питагоре.

Поставља се питање зашто онда прича каже - појава Питагорина теорема припада њему? Одговор може бити само један - он је доказао однос ширине и висине у троуглу. Учинио је оно што су пре неколико векова они који су једноставно користили однос аспеката и хипотенуза емпиријски успостављени.
Из живота Питагоре
Футуре греат научник, математичар, Филозоф је рођен на острву Самос 570. пне. Историјски документи сачували су податке о оцу Питагоре, који је био резбар за драгоцено камење, али нема информација о мајци. Речено је о дечаку који је рођен да је изванредно дете које је показивало страст према музици и поезији још од детињства. Историчари приписују учитеље младог Питагоре Хердомаданту и Ферекиду од Сироса. Први је увео дјечака у свијет муза, а други, као филозоф и оснивач талијанске филозофске школе, усмјерио је младићев поглед према логосу.
Са 22 године (548. пне. Е.) Питагора је отишао у Ноократис да проучи језик и религију Египћана. Даље, његов пут је лежао у Мемфису, где је, захваљујући свештеницима, након што је прошао кроз своје генијалне тестове, схватио египатску геометрију, која је можда подстакла радозналог младића да докаже Питагорину теорему. Историја ће ову теорему приписати теореми у будућности.

Заробљен од краља Вавилона
На путу кући у Хеллас, Питагора је ухваћен од стране краља Вавилона. Али бити у заточеништву користио је знатижељни ум математичара почетника, он је имао нешто да научи. Заиста, у тим годинама, математика у Вавилону је била развијенија него у Египту. Провео је дванаест година проучавајући математику, геометрију и магију. И вероватно је то била Вавилонска геометрија која је била укључена у доказивање односа аспекта троугла и историје открића теореме. Питагора је имао довољно знања и времена за то. Али да се то догодило у Вавилону, нема документарне потврде или оповргавања.
530 год Питагора бјежи из заточеништва у своју домовину, гдје живи на двору тиранина Поликрат у статусу полу-плоче. Такав живот не одговара Питагори, и он се повлачи у пећине на Самосу, а затим одлази на југ Италије, где се у то време налазила грчка колонија Кротон.
Тајни монашки ред
На основу ове колоније, Питагора је организовао тајни монашки ред, који је истовремено био и религиозна заједница и научно друштво. Ово друштво је имало своју властиту повељу, која се односила на поштовање одређеног начина живота.

Питагора је тврдио да, да би разумио Бога, особа мора научити такве науке као алгебра и геометрија, знати астрономију и разумети музику. Истраживачки рад је сведен на познавање мистичне стране бројева и филозофије. Треба напоменути да принципи које је у то време проповедао Питагора имају смисла чак и сада.
Многа открића која су начинили ученици Питагоре приписана су њему. Ипак, ако кратко говоримо, историја стварања Питагорина теорема од стране античких историчара и биографа тог времена, директно је повезана са именом овог филозофа, мислиоца и математичара.
Учења Питагоре
Можда је помисао на повезаност теореме са именом Питагоре навела историчаре да кажу велики Грк да су сви феномени нашег живота кодирани у ноторном троуглу његовим ногама и хипотенуза. И овај троугао је "кључ" за решавање свих проблема који се појављују. Велики филозоф је рекао да треба видети троугао, онда можемо претпоставити да је проблем две трећине решен.

Питагора је говорио о свом учењу само вербално својим ученицима, не правећи никакве белешке, чувајући тајну. Нажалост, учење највећег филозофа до данас није преживело. Нешто од њега је исцурило, али се не може рећи колико је истина, и колико је погрешно у ономе што је постало познато. Чак и са историјом Питагорине теореме, није све неоспорно. Историчари математике сумњају у ауторство Питагоре, по њиховом мишљењу, теорема је коришћена много векова пре њеног рођења.
Питагорина теорема
Може се чинити чудним, али не постоји историјски доказ о теореми самог Питагоре - не у архиви, нити у било којим другим изворима. У модерној верзији сматра се да припада никоме осим Еуклиду.
Постоје докази да је један од највећих историчара математике, Моритз Цантор, открио на папирусу похрањеном у Берлинском музеју, који су забиљежили Египћани око 2300. пне. е. равноправност, која гласи: 3² + 4² = 5².
Укратко из историје Питагорине теореме
Формулација теореме из еуклидских "принципа", у преводу, звучи исто као иу модерној интерпретацији. У њему нема новог очитавања: квадрат супротне стране правог угла једнак је збиру квадрата страна поред правог угла. Чињеница да су древне цивилизације Индије и Кине користиле теорему потврђена је и трактатом Зхоу - би суан јин. Садржи информације о египатском троуглу, који описује однос ширине и висине 3: 4: 5.

Не мање интересантна је и друга кинеска математичка књига, Цху-Пеи, која такође спомиње Питагорин троугао са објашњењем и цртежима који се подударају са цртежима хиндуистичке геометрије Басхаре. О самом троуглу у књизи пише да ако се прави угао може разложити на његове саставне делове, онда ће линија која спаја крајеве страна бити једнака пет, ако је основа три, а висина четири.
Индијска расправа "Сулва Сутра", која датира још од ВИИ-В века пре нове ере. е., говори о изградњи правог угла помоћу египатског троугла.
Доказ теореме
У средњем веку, студенти су доказ теорема сматрали претешким. Слаби студенти су памтили теореме напамет, без разумевања значења доказа. У том смислу, добили су надимак "магарци", јер је Питагорина теорема за њих била непремостива препрека, као мост за дупе. У средњем веку, ученици су дошли са шаљивим стихом на тему ове теореме.
Да би се доказао Питагорин теорем на најлакши начин, треба једноставно измјерити његове стране, без употребе концепта квадрата у доказу. Дужина стране наспрам правог угла је ц, а суседни а и б, као резултат добијамо једначину: а 2 + б 2 = ц 2 . Ова изјава, као што је горе поменуто, потврђена је мерењем дужина страна правог троугла.
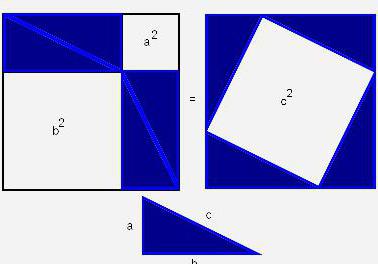
Ако покренемо доказ теореме узимајући у обзир површину правоугаоника изграђених на странама троугла, можемо одредити површину целе фигуре. Она ће бити једнака површини квадрата са страном (а + б), а са друге стране, сумом површина четири троугла и унутрашњег квадрата.
(а + б) 2 = 4 к аб / 2 + ц 2 ;
а 2 + 2аб + б 2 ;
ц 2 = а 2 + б 2 , по потреби.
Практични значај Питагорине теореме је да се може користити за проналажење дужина сегмената без њиховог мерења. Приликом изградње објеката израчунавају се удаљености, положај носача и греда, одређују се центри гравитације. Питагорина теорема се користи у свим модерним технологијама. Нисмо заборавили теорему приликом креирања филмова у 3Д-6Д-димензијама, где се поред 3 уобичајене вредности узимају у обзир висина, дужина, ширина - време, мирис и укус. Како су укуси и мириси повезани са теоремом - питате? Веома је једноставно - када покажете филм, потребно је да израчунате где и шта мирише и укусе шаље у аудиторијум.
Да ли ће и даље бити. Неограничени простор за откривање и стварање нових технологија чека на размишљање.