Закони геометријске оптике и њихова употреба у сферним огледалима и танким сочивима

Понашање светлосних зрака док пролазе кроз различите прозирне медије може се јединствено одредити без познавања природе саме светлости. Оваквим задацима управља посебна грана физике - геометријска оптика. Његови закони се разматрају у овом чланку.

Својства свјетлосних зрака у геометријској оптици

По особинама зрака у овом дијелу физичари разумију особитости њиховог кретања у прозирним медијима. Нарочито, када се креће светлосни сноп у хомогеном медију, следеће тврдње су тачне:

• пут светлости је равна линија;
• пресецајућа два светлосна снопа не ступају у међусобну интеракцију;
• материјални медиј одређује брзину светлости у њему.

Ова својства су фундаментална за било који електромагнетни талас. Захваљујући њима, изведени су основни закони геометријске оптике за феномене:

• рефлексије;
• рефракција

Принцип фарме

У ствари, то је директна последица закона правоцртног ширења светлости у хомогеном транспарентном материјалу. Овај принцип утврђује да светлост током процеса рефлексије и преламања бира такву путању од једне до друге тачке у простору, коју може превазићи у најкраћем времену.

Принцип најмањег времена формулисао је француски научник Пјер Фермат почетком 1660-их. Због Ферматовог принципа, закони геометријске оптике повезани са феноменом рефракције и рефлексије, добили су математичко оправдање. Занимљиво је напоменути да су ти закони већ били познати из 1600-тих. Што се тиче Пиерреа Фермата, иако је наведено начело најкраћег времена носило његово презиме, он је формулисан много прије Француза (барем за феномен рефлексије). То је урадио грчко-египатски филозоф Херон из Александрије у првом веку наше ере.

Из Ферматовог принципа недвосмислено следи да се у хомогеном медију светлост мора кретати дуж равне путање (закон праволинијског ширења светлости). Ако медиј није хомоген, онда ће се светлост ширити дуж одређене кривуље, али принцип најкраћег времена неће бити нарушен. Користећи га, лако се могу извести математичке формулације за феномене рефлексије и рефракције, које су добијене генерализацијом великог броја експерименталног материјала.

Процеси лома и рефлексије светлости и њихов математички опис

Оба ова феномена карактерише чињеница да сноп светлости у једној тачки драстично мења своју путању. То се дешава зато што у овом тренутку наилази на препреку на свом путу. Ако је ова препрека непровидан материјал, тада се јавља један процес рефлексије. Ако је препрека прозирна, онда се поред рефлектованог снопа појављује и ломљени.

Претпоставимо да је препрека равна површина. Нека раздвоји два транспарентна медија. Кроз тачку упадања зрака на површину, повлачимо окомито на њу (нормални Н). Вектор инцидентног зрака је означен са р ₁ ¯, вектор рефлектованог зрака је р ₂ ¯, а преломљени је р ₃ ¯. Угао између р ₁ ¯ и Н је означен са θ ₁ , између р ₂ ¯ и Н - θ ₂ , и на крају између р ₃ ¯ и Н - θ ₃ . Експериментално су успостављене следеће везе:

1. Вектор зраци р ₁ ¯, р ₂ ¯, р ₃ ¯ и окомити Н леже у истој равни.
2. Угао упада θ ₁ и угао рефлексије θ ₂ су једнаки.
3. Угао преламања θ ₃ се односи на θ ₁ односом н ₁ * син (θ ₁ ) = н ₂ * син (θ ₃ ).

Ова формула се назива Снеллов закон у част холандског научника Виллеброрда Снелла. Сам Снелл га је примио у смислу удаљености. Кроз синусе углова, Рене Десцартес је забиљежио нешто касније, па се у земљама које говоре француски то назива Снелл-Десцартесов закон. Симболи н ₁ и н ₂ су апсолутни индекси преламања медија, који се одређују односом брзине светлости у вакууму према брзини у одговарајућем материјалу.

Ови односи се обично називају закони рефлексије и преламања геометријске оптике.

Равна и сферна огледала

За геометријске конструкције слика у огледалима користе се закон правоцртне пропагације светлости и закон рефлексије. У овом случају, огледала могу бити не само равна, већ и конвексна и конкавна.

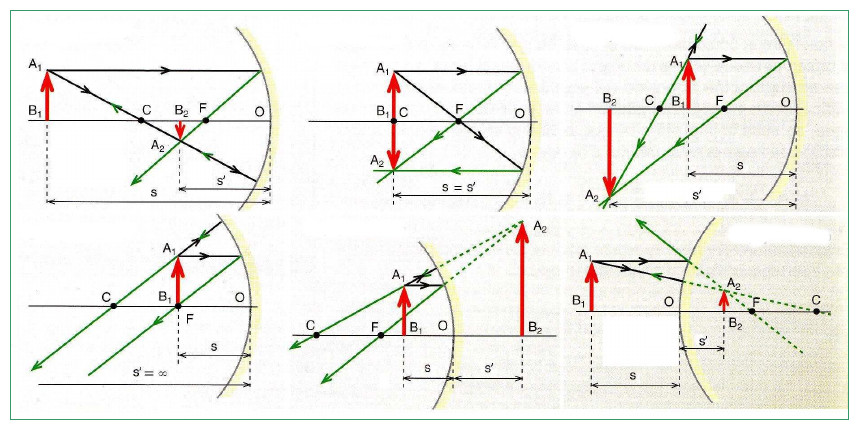
Лако је научити да самостално градимо слике у огледалима било ког типа. Потребно је само разумети како зраке реагују са оптичким уређајем. Дакле, сноп који долази из фокуса увек се рефлектује од огледала паралелног са оптичком осом, а сноп који пролази кроз центар огледала (дуж радијуса) се рефлектује у супротном смеру.

Различити случајеви положаја објекта у односу на оптички уређај и техника израде слика у конкавним и конвексним огледалима приказани су на слици испод.

Танке леће

Ово је још један оптички уређај, чији је принцип заснован на основним законима геометријске оптике. Танка лећа је објекат направљен од прозирног материјала и омеђен са две површине. Једна од површина мора бити сегмент кугле.

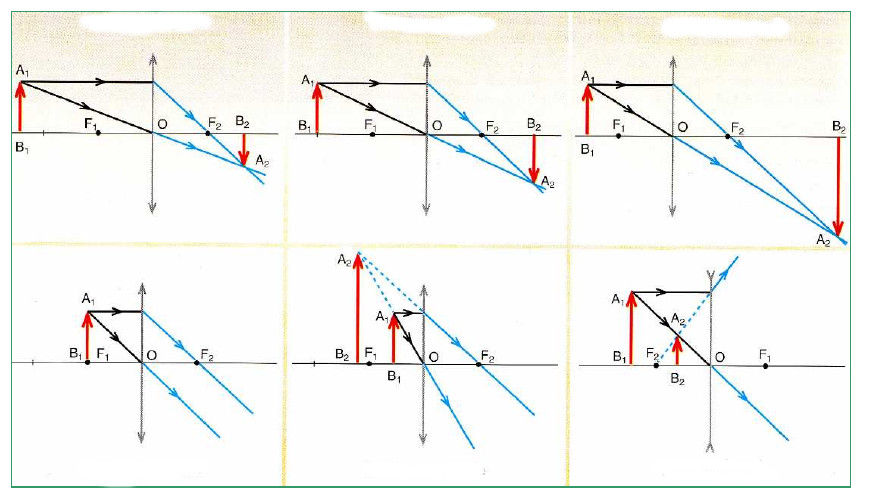
Објективи се сакупљају (паралелни зраци конвергирају у фокусу иза сочива) и расипање (имагинарни наставци паралелних зрака се концентрирају у фокусу испред објектива).

Принцип изградње слика у њима је готово исти као у сферним огледалима. Различити случајеви су приказани на слици испод.

Око као оптички уређај

Између осталог, закони геометријске оптике се користе за проучавање принципа људског ока и прилагођавање визије.

Око је сложен оптички систем са позитивном силом, тј. Може се заменити еквивалентним сакупљачем. Ако је оштећење ока отежано (смјештај доводи до промене оптичке моћи ока, посебно леће), онда се мутна слика формира на ретини померањем фокуса иза ретине (далековидност) или напред из ње (миопија). Корекција се врши додавањем (одузимањем) диоптрије у систем ока како би се фокус вратио на ретину. Да бисте то урадили, користите наочаре, леће или ласерску корекцију вида.