Пројекција тачке у равни. Пројекција тачке на правој линији у равни
Проучавање својстава фигура у простору и на равнини је немогуће без познавања удаљености између тачке и таквих геометријских објеката као што су правац и раван. У овом чланку ћемо показати како пронаћи те удаљености, узимајући у обзир пројекцију тачке на равнини и на правој линији.
Једначина линије за дводимензионалне и тродимензионалне просторе
Израчунавање удаљености тачке од правца и равнине врши се помоћу његове пројекције на те објекте. Да би се пронашле те пројекције, треба знати у ком облику су дате једначине за равне линије и равни. Почнимо од првог.
Равна линија је скуп тачака, од којих се свака може добити из претходног преношењем на паралелне векторе. На пример, постоји тачка М и Н. Вектор МН цоннецтинг који их повезује узима М до Н. Постоји и трећа тачка П. Ако је вектор МП¯ или НП¯ паралелан са МН¯, онда све три тачке на једној линији леже и формирају је.
У зависности од димензије простора, једначина која одређује линију може да промени свој облик. Дакле, добро позната линеарна зависност и координате на к у простору описује равни која је паралелна са трећом з осом. У том смислу, у овом чланку ћемо размотрити само векторску једначину за ту линију. Има исти изглед за равни и тродимензионални простор.
У простору, правац се може дефинисати следећим изразом:
(к; и; з) = (к 0 ; и 0 ; з 0 ) + α * (а; б; ц)
Овде, координатне вредности са нултим индексима одговарају равној линији одређене тачке, у¯ (а; б; ц) је координата вектора за усмеравање који лежи на датој правој линији, α је произвољни реални број, који мења све тачке праве линије. Ова једначина се назива вектор.
Често се горе наведена једначина пише у отвореном облику:
к = к 0 + а * а;
и = и 0 + α * б;
з = з 0 + α * ц
Слично томе, можемо да напишемо једначину за равну линију у равни, тј. У дводимензионалном простору:
(к; и) = (к 0 ; и 0 ) + α * (а; б);
к = к 0 + а * а;
и = и 0 + α * б
Плане екуатион
Да бисте могли да пронађете раздаљину од тачке до равни пројекција, морате знати како је дефинисана равнина. Као и правац, може се представити на више начина. Овде разматрамо само једну: општу једначину.
Претпоставимо да тачка М (к 0 ; и 0 ; з 0 ) припада равни, а вектор н ¯ (А; Б; Ц) је окомит на њу, онда ће за све тачке (к; и; з) равни следећа једнакост бити истинита:
А * к + Б * и + Ц * з + Д = 0, где је Д = -1 * (А * к 0 + Б * и 0 + Ц * з 0 )
Треба имати на уму да су у овој опћој једнаџби равнине коефицијенти А, Б и Ц координате нормале на равнину вектора.
Израчунавање удаљености помоћу координата
Пре него што пређемо на разматрање пројекција на равни једне тачке и на правој линији, треба подсетити како треба израчунати растојање између две познате тачке.
Претпоставимо да постоје две просторне тачке:
А 1 (к 1 ; и 1 ; з 1 ) и А 2 (к 2 ; и 2 ; з 2 )
Тада се удаљеност између њих израчунава по формули:
А 1 А 2 = √ (((к 2 -к 1 ) 2 + (и 2 -и 1 ) 2 + (з 2 -з 1 ) 2 )
Користећи овај израз, одређује се и дужина вектора А 1 А 2 ¯.
За случај на равнини, када су дате две тачке са само пар координата, можете написати сличну једначину без присуства члана са з у њему:
А 1 А 2 = √ (((к 2 -к 1 ) 2 + (и 2 -и 1 ) 2 )
Сада ћемо размотрити различите случајеве пројекције на равни тачке на правој линији и на равни у простору.
Тачка, линија и удаљеност између њих
Претпоставимо да постоји нека тачка и правац:
П 2 (к 1 ; и 1 );
(к; и) = (к 0 ; и 0 ) + α * (а; б)
Размак између ових геометријских објеката одговара дужини вектора, чији почетак лежи у тачки П 2 , а крај је у таквој тачки П на назначеној правој линији, за коју је вектор П 2 П ¯ ове праве окомите. Тачка П се назива пројекција тачке П 2 на дотичну линију.
На доњој слици приказана је тачка П 2 , њена удаљеност д до праве линије, као и вектор правца в 1 ¯. Такође, на линији се бира произвољна тачка П 1 и вектор се повлачи из њега у П 2 . Тачка П овде се поклапа са местом где окомица пресеца линију.
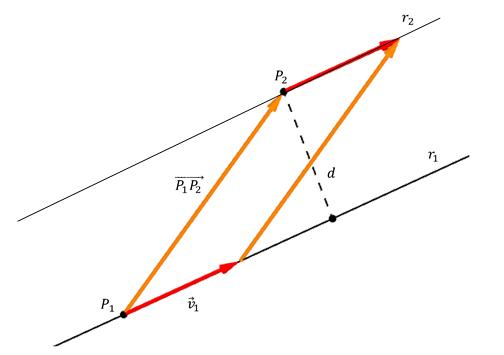
Видљиво је да наранџасте и црвене стрелице формирају паралелограм чије су стране вектор П 1 П 2 ¯ и в 1 ¯, а висина д. Из геометрије је познато да је за проналажење висине паралелограма његова површина подељена дужином базе, на којој је спуштена окомица. Пошто је површина паралелограма израчуната као векторски производ његових страна, добијамо формулу за израчунавање д:
д = | [П 1 П 2 ¯ * в 1 ¯] | / | в 1 ¯ |
Сви вектори и координате тачака у овом изразу су познати, тако да их можете користити без икаквих трансформација.
Могуће је да се овај проблем реши другачије. Да бисте то урадили, запишите две једначине:
- скаларни производ П 2 П ¯ на в 1 ¯ треба да буде једнак нули, јер су ти вектори међусобно окомити;
- координате тачке П морају задовољити једнаџбу линије.
Ове једначине су довољне да се пронађу координате П, а затим дужина д по формули датој у претходном параграфу.
Задатак проналажења удаљености између линије и тачке
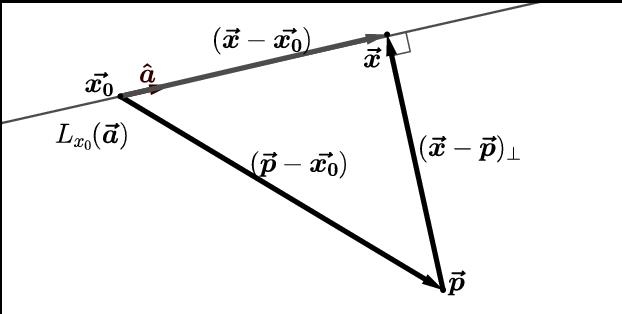
Показујемо како користити те теоријске информације за рјешавање одређеног проблема. Претпоставимо да су следећа тачка и линија познати:
М (5; -3);
(к; и) = (3; 1) - α * (0; 2)
Неопходно је пронаћи тачке пројекције на равној линији, као и удаљеност од М до праве линије.
Означити пројекцију која се налази у тачки М 1 (к 1 ; и 1 ). Овај проблем решавамо на два начина, како је описано у претходном параграфу.
Метод 1. Вектор правца в 1 ¯ координате има (0; 2). Да бисте направили паралелограм, изаберите тачку која припада правој линији. На пример, тачка са координатама (3; 1). Тада ће вектор друге стране паралелограма имати координате:
(5; -3) - (3; 1) = (2; -4)
Сада је потребно израчунати продукт вектора који дефинирају стране паралелограма:
[(2; -4) * (0; 2)] = 4
Заменимо ову вредност у формули, добијамо растојање д од М до праве:
д = 4 / =4 = 2
Метод 2. Сада ћемо на други начин пронаћи не само удаљеност, већ и координате пројекције М на линији, како то захтијева стање проблема. Како је горе поменуто, за решавање проблема потребно је креирати систем једнаџби. Изгледаће као:
(к 1 -5) * 0 + (и 1 +3) * 2 = 0;
(к 1 ; и 1 ) = (3; 1) -α * (0; 2)
Ми решавамо овај систем:
и 1 = -3;
к 1 = 3
Пројекција почетне тачке координате је М 1 (3; -3). Тада је потребна удаљеност:
д = | ММ 1 ¯ | = √ (4 + 0) = 2
Као што видите, оба решења су дала исти резултат, што указује на исправност изведених математичких операција.
Пројекција тачке на равни
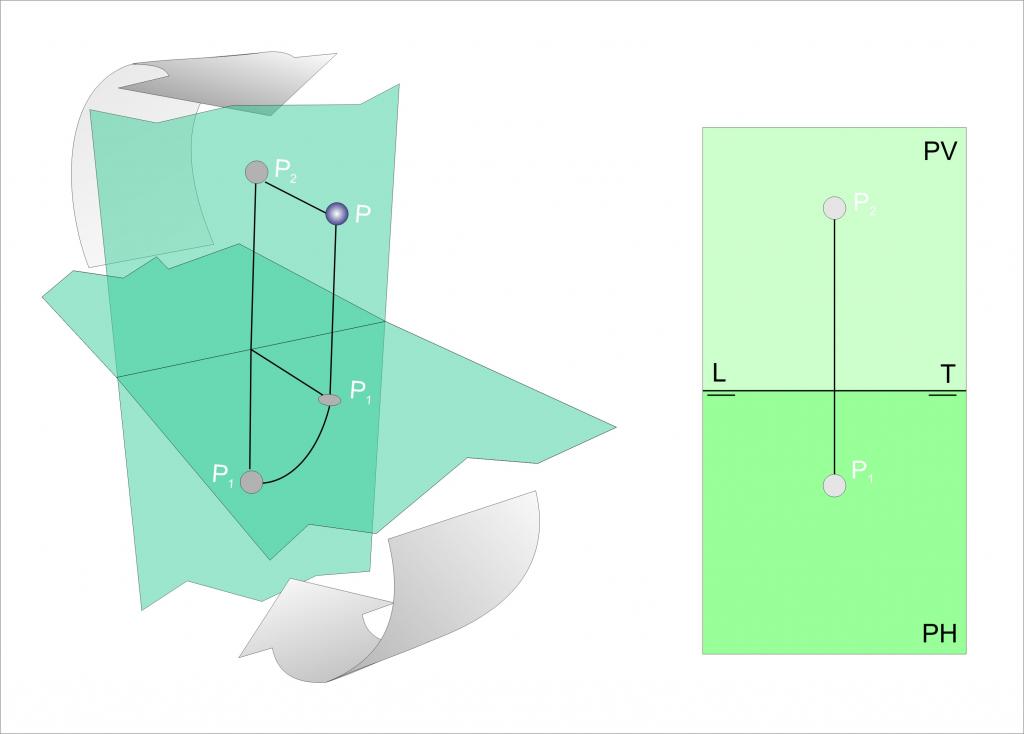
Сада размислите шта је пројекција тачке дате у простору на одређеној равни. Лако је претпоставити да је ова пројекција и тачка, која заједно са првобитном формира вектор који је окомит на раван.
Претпоставимо да пројекција на равнину координата М тачке има следеће:
М 1 (к 1 ; и 1 ; з 1 )
Сама равнина описана је једнаџбом:
А * к + Б * и + Ц * з + Д = 0
На основу ових података, можемо направити једнаџбу праве линије која прелази раван под правим углом и пролази кроз М и М 1 :
(к; и; з) = (к 0 ; и 0 ; з 0 ) + α * (А; Б; Ц)
Овдје су варијабле с нултим индексима координате точке М. Могуће је израчунати положај на равнини точке М 1 уз претпоставку да њене координате морају задовољити обје писане једнаџбе. Ако ове једначине нису довољне за решавање проблема, онда се може користити услов паралелизма ММ 1 ¯ и вектор правца за дату раван.
Очигледно, пројекција тачке која припада једној равни се поклапа са самом собом, а одговарајућа удаљеност је нула.
Задатак са тачком и авионом
Нека је дата тачка М (1; -1; 3) и раван, која је описана следећом општом једначином:
-к + 3 * и -2 * з + 4 = 0
Потребно је израчунати координате пројекције у равнини тачке и израчунати растојање између тих геометријских објеката.
За почетак, конструишемо једначину линије која пролази кроз М и окомита на наведену раван. Изгледа као:
(к; и; з) = (1; -1; 3) + α * (- 1; 3; -2)
Означимо тачку где ова правац сека раван, М1. Једнакости за раван и правац морају бити задовољени ако замјенимо М 1 координате у њима. Пишући експлицитно из једначине праве линије, добијамо следеће четири једначине:
-к 1 + 3 * и 1 -2 * з 1 + 4 = 0;
к 1 = 1 - α;
и 1 = -1 + 3 * α;
з 1 = 3 - 2 * α
Из последње једнакости добијамо параметар α, затим га замењујемо у претпоследњем и другом изразу, добијамо:
а = (3-з 1 ) / 2;
и 1 = -1 + 3 * (3-з 1 ) / 2 = -3 / 2 * з 1 + 3.5;
к 1 = 1 - (3-з 1 ) / 2 = 1/2 * з 1 - 1/2
Израз за и 1 и к 1 замењује се једначином за раван, имамо:
-1 * (1/2 * з 1 - 1/2) + 3 * (- 3/2 * з 1 + 3.5) -2 * з 1 + 4 = 0
Где добијамо:
з 1 = 15/7
Затим:
и 1 = -3 / 2 * 15/7 + 3.5 = 2/7;
к 1 = 1/2 * 15/7 - 1/2 = 4/7
Утврдили смо да пројекција тачке М на датој равни одговара координатама (4/7; 2/7; 15/7).
Сада израчунајте удаљеност | ММ 1 ¯ |. Координате одговарајућег вектора су:
ММ 1 ¯ (-3/7; 9/7; -6/7)
Потребна удаљеност је:
д = | ММ 1 ¯ | = /126 / 7 ≈ 1.6
Три тачке пројекције
Приликом израде цртежа често је потребно добити пројекције секција на међусобно окомите три равни. Стога је корисно размотрити шта ће бити једнаке пројекцијама одређене тачке М са координатама (к 0 ; и 0 ; з 0 ) на три координатне равни.

Није тешко показати да је ки равнина описана једнаџбом з = 0, кз равнина одговара изразу и = 0, а преостала из равнина означена је једнакошћу к = 0. Лако је претпоставити да ће пројекције тачке на 3 равнине бити једнаке:
за к = 0: (0; и 0 ; з 0 );
за и = 0: (к 0 ; 0; з 0 );
за з = 0: (к 0 ; и 0 ; 0)
Где је важно знати пројекције тачке и њене удаљености од равни?
Одређивање положаја пројекције тачака на датој равни је важно при проналажењу таквих величина као што су површина и запремина косих призми и пирамида. На пример, растојање од врха пирамиде до равни базе је висина. Ово последње је укључено у формулу за обим ове бројке.
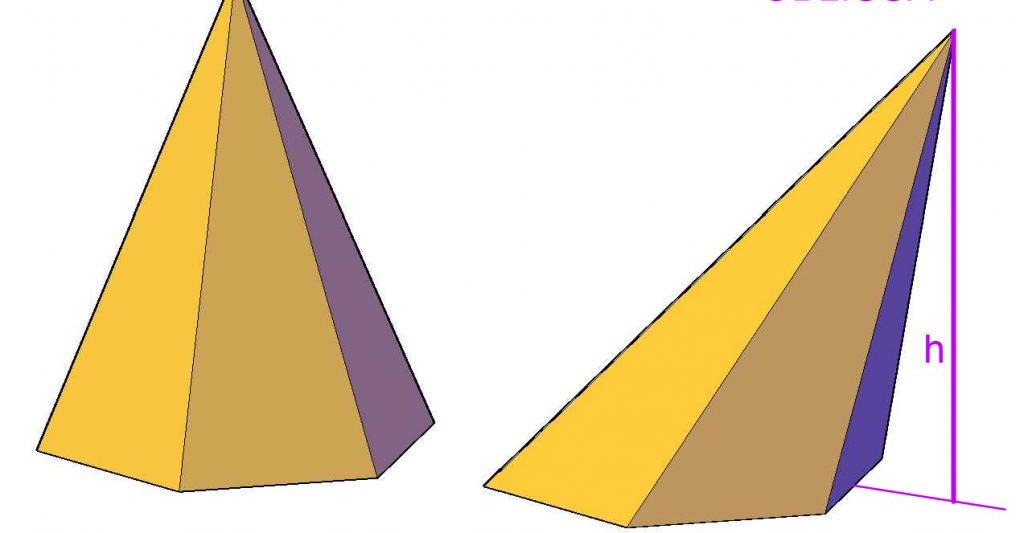
Разматране формуле и методе за одређивање пројекција и растојања од тачке до праве линије и равни су прилично једноставне. Важно је само запамтити одговарајуће облике равнинских и директних једначина, као и имати добру просторну имагинацију како би их успјешно примијенили.