Транслационно кретање: дефиниција, формуле, теорема
Механика разматра све могуће помаке материјалне тачке и чврстог тела. Све су описане у неколико одељака. На пример, питање како ће се кретати биће прерогатив кинематике. Он детаљно описује транслационо кретање, као и сложеније - ротационо. Прво, то је лакше. Јер без тога је тешко прећи на следеће теме.
Које претпоставке допушта механичар?
У многим проблемима дозвољено је увести апроксимацију. То је због чињенице да неће утицати на резултат, али ће поједноставити ток расуђивања.
Прва апроксимација се односи на величину тела. Ако је тело које се разматра значајно мање од осталих у истом референтном оквиру, онда се његове димензије занемарују. И тело се претвара у материјалну тачку.
Други следи из одсуства деформација у телу током његовог кретања. Или чак и тако безначајне величине, које се могу потпуно занемарити.

Шта је транслаторно кретање тела?
Ради појашњења, мораћете да размотрите било које две тачке унутар чврстог дела. Треба да повежу сегмент. Ако овај сегмент остане паралелан са почетном позицијом током кретања, онда се каже да је то кретање напред.
Ако постоји занемаривање величине тела и узима се у обзир материјална тачка Овај сегмент је одсутан и креће се дуж саме линије.
Живописни примери таквог покрета
Прва ствар коју треба запамтити је колица за лифт. Савршено илуструје кретање тела напред. Лифт се увек помера само горе или доле без икакве ротације.
Следећи пример који илуструје транслационо кретање је кретање кабине Феррисовог точка. Међутим, ово је стварно само у ситуацији када се благи нагиб кабине на почетку сваког помака не узима у обзир.
Трећа ситуација, када је могуће говорити о кретању напред, повезана је са кретањем педала за бицикле. Њихово кретање се сматра релативно у односу на оквир. И овде се уводи претпоставка да се стопала особе не љуљају док јашу.
Листа се може завршити померањем клипова, који осцилирају унутар цилиндара мотора са унутрашњим сагоревањем.

Главни концепти
Кинематика транслационог кретања је да проучава и описује кретање чврстих и материјалних тачака. Међутим, она не узима у обзир разлоге који присиљавају тијело на то. Да би описали кретање, координате ће бити потребне да означе своју позицију у простору. Поред тога, потребно је познавати брзину и то у сваком тренутку.
Прво, вреди се сетити путање. То је линија дуж које се тело померило.
Први је да уђете у потез. То је вектор, који је означен латиничним словом р. Може повезати поријекло са положајем материјалне точке. У другим случајевима, овај вектор је нацртан од почетне до крајње тачке путање. Јединице помака су метри.
Друга вредност која заслужује пажњу је начин. Она је једнака дужини путање којом се тело померило. Пут је означен словом латиница С, који се такође мери у метрима.

Основне формуле
Сада је време да се убрза. Она је такође вектор. Штавише, она карактерише не само правац кретања тела, већ и брзину његовог кретања. Вектор брзине је увек усмерен дуж тангентне линије, која се може повући у било коју тачку путање. Означава се словом В. Јединице њеног мерења су м / с.
Брзина у сваком тренутку покрета може се дефинисати као дериват кретања током времена. Ако је проблем у питању униформно кретање, онда је важећа следећа формула:
- В = С: т, где је т време кретања.
У ситуацији када се смер кретања мења, морате користити суму свих покрета.
Следећа вредност је убрзање. Поново, векторска количина, која је усмерена ка брзини са великом вредношћу. Дефинише се као први дериват брзине током времена. Прихваћена ознака - слово "а". Димензија је назначена у м / с 2 .
Формуле за сваку компоненту убрзања, усмерене дуж оса, израчунате су као однос промене брзине дуж ове осе према временском интервалу. Ако направите математички запис, добићете следеће:
- и к = кВ к : .т.
За пројекције убрзања на друге оси, формуле су сличне.
Поред тога, када се разматра кретање дуж путање са кривинама, могуће је да се вектор убрзања разложи на два термина:
- а = а т + а н , где је т тангенцијално убрзање усмерено дуж тангенте савијања, а н је нормално, што указује на центар кривине.
Транслационо кретање било ког чврстог тела сведено је на описивање кретања само једне његове тачке. Формуле које се користе су:
- С = С 0 + В 0 т + (при 2 ): 2.
- В = В 0 + ат.
У овој формули, индекси "нула" означавају почетне вредности количина.
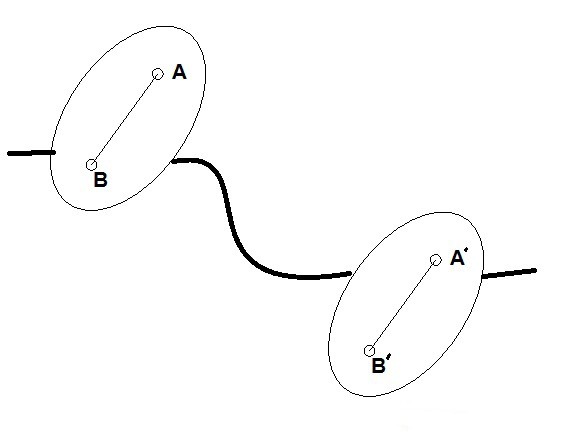
Транслатионал магнитуде тхеорем
Његова формулација је следећа: путања, брзина и убрзање свих тачака тела су исте током кретања напред.
Да бисте то доказали, морате написати формулу вецтор аддитионс померање и вектор који повезује две произвољне тачке. Трајекторије свих тачака добијају се због њиховог преноса дуж другог вектора. И то не мења свој правац и величину током времена. Према томе, може се тврдити да се све тачке тела крећу дуж истих путања.
Ако узмемо временски дериват, добијемо вредност брзине. Штавише, израз је поједностављен до те мере да су брзине две тачке једнаке.
Поље другог временског деривата је резултат једнакости убрзања двију тачака.