Тригонометрија од нуле: основни појмови, историја

Синус, косинус, тангента - када изговарате ове речи у присуству средњошколаца, можете бити сигурни да ће две трећине њих изгубити интерес за даље разговоре. Разлог лежи у чињеници да се основе тригонометрије у школи предају у потпуној изолацији од стварности, те стога ученици не виде смисао у проучавању формула и теорема.

У ствари, при ближем разматрању, ова област знања се испоставља веома интересантном, као и примењена - тригонометрија проналази примену у астрономији, грађевинарству, физици, музици и многим другим областима.

Упознајмо се са основним концептима и навешћемо неколико разлога за проучавање овог одељка математичке науке.

Хистори оф

Није познато када је човечанство почело да ствара будућу тригонометрију од нуле. Међутим, документовано је да су Египћани већ у другом миленијуму пре нове ере познавали основе ове науке: археолози су пронашли папирус са задатком у коме је неопходно да се пронађе угао нагиба пирамиде на две познате стране.

Озбиљнији успех постигли су научници древног Вавилона. Током векова, бавећи се астрономијом, савладали су бројне теореме, увели посебне начине за мерење углова, које ми, успут, данас користимо: степени, минуте и секунде позајмили су европска наука у грчко-римској култури, у којој су ове јединице дошле од Бабилонаца.

Претпоставља се да је позната Питагорина теорема, која се односи на основе тригонометрије, позната Бабилонцима пре скоро четири хиљаде година.

Име

Дословно, израз "тригонометрија" може се превести као "мјерни трокут". Главни предмет истраживања у овом делу науке је био вековима правоугаони троугао или боље речено, однос између магнитуда углова и дужина његових страна (данас проучавање тригонометрије од нуле почиње овим одељком). Често се дешавају ситуације у животу када је немогуће практично измјерити све потребне параметре неког објекта (или удаљености до објекта), а онда постаје неопходно добити податке који недостају помоћу калкулација.

На пример, у прошлости, особа није могла да измери удаљеност до просторни објекти али покушаји да се израчунају ове удаљености се догађају много прије појаве наше ере. Тригонометрија је такође одиграла важну улогу у навигацији: имајући неко знање, капетан је увек могао да се креће ноћу по звездама и да прилагоди курс.

Основни концепти

Да бисте савладали тригонометрију од нуле, морате разумети и запамтити неколико основних појмова.

Синус одређеног угла је однос супротне ноге и хипотенузе. Појашњавамо да је супротна нога страна супротна од угла који разматрамо. Према томе, ако је угао 30 степени, синус овог угла ће увек, за било коју величину троугла, бити ½. Косинус кута је однос суседне ноге према хипотенузи.

Тангента је однос супротне ноге према суседном (или, еквивалентно, однос синуса и косинуса). Котангенс је јединица подељена тангентом.

Вриједи споменути чувену Пи (3.14 ...), која представља половину опсег са радијусом једне јединице.

Популар бугс

Људи који студирају тригонометрију од нуле праве низ грешака - углавном из непажње.

Прво, приликом рјешавања проблема у геометрији, треба имати на уму да је употреба синуса и косинуса могућа само у правокутном трокуту. Дешава се да ученик “на машини” узме најдужу страну троугла за хипотенузу и добије нетачне резултате прорачуна.

Друго, у почетку је лако збунити вредности синуса и косинуса за изабрани угао: подсетимо да је синус од 30 степени нумерички једнак косинусу од 60, и обрнуто. Када замените погрешан број, сви даљњи прорачуни ће бити погрешни.

Треће, док се проблем не ријеши у потпуности, не бисте требали заокружити вриједности, извадити коријене, записати обичан дио као децималу. Често ученици настоје да добију „леп“ број у проблему тригонометрије и одмах извлаче корен из три, иако се у једном кораку овај корен може смањити.

Етимологија речи "синус"

Историја речи "синус" је заиста необична. Чињеница је да дословни превод ове ријечи из латинског значи "шупаљ". То је зато што је исправно разумевање речи изгубљено приликом превођења са једног језика на други.

Називи основних тригонометријских функција потичу из Индије, где је појам синуса означен речју "тетива" на санскрту - чињеница је да сегмент заједно са луком круга на којем је заснован личи на лук. Током врхунца арапске цивилизације, позајмљена су индијска достигнућа у области тригонометрије, а термин је пренешен на арапски у облику транскрипције. Десило се да је на овом језику већ постојала слична реч која означава шупљину, а ако су Арапи разумели фонетску разлику између изворне и позајмљене речи, онда су Европљани који су превели научне трактате на латински дословно превели арапску реч, нема везе са концептом синуса . Ми их користимо до данас.

Табеле вредности

Постоје табеле у које се уносе нумеричке вредности за синус, косинус и тангенте свих могућих углова. У наставку су представљени подаци за углове од 0, 30, 45, 60 и 90 степени, који се морају научити као обавезни дио тригонометрије за лутке, а корист од памћења је прилично једноставна.

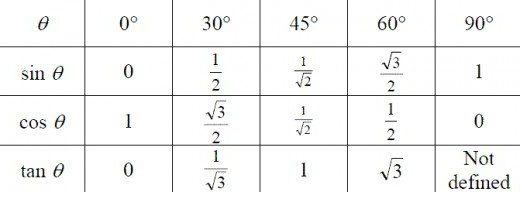Ако се деси да је нумеричка вредност синусног или косинусног угла "излетела из главе", постоји начин да се то сам извуче.

Геометријска репрезентација

Нацртајте круг, кроз његов центар нацртамо абсцису и ординате осе. Оса апсцисе се налази хоризонтално, а оса ординате је вертикална. Обично су потписани као “Кс” и “И”, респективно. Сада из центра круга цртамо линију на такав начин да добијемо потребан угао између њега и Кс оси. Коначно, од тачке где се линија сијече у круг, спуштамо окомицу на Кс. Дужина резултујућег сегмента биће једнака нумеричкој вредности синуса нашег угла.

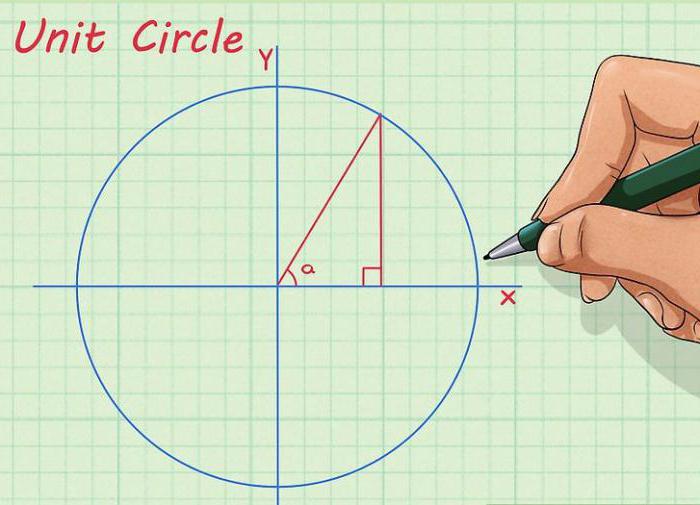Овај метод је веома релевантан ако сте заборавили жељену вредност, на пример, на испиту, и нема уџбеника о тригонометрији при руци. Нећете добити тачну цифру на овај начин, али дефинитивно ћете видети разлику између ½ и 1.73 / 2 (синус и косинус угла од 30 степени).

Апплицатион

Један од првих специјалиста који су користили тригонометрију били су морнари који нису имали никакву другу референтну тачку на отвореном мору, осим неба изнад њихових глава. Данас су капетани бродова (авиони и друго) врсте транспорта) Они не траже најкраћи пут кроз звезде, али активно користе ГПС навигацију, што би било немогуће без употребе тригонометрије.

У скоро сваком физика Чекате калкулације помоћу синуса и косинуса: да ли је то примена силе у механици, рачунање путање објеката у кинематици, осцилације, ширење таласа, преламање светлости - не можете без основне тригонометрије у формулама.

Друга професија која је незамислива без тригонометрије је геодет. Користећи теодолит и ниво или сложенији уређај - тахиометар, ови људи мере разлику у висини између различитих тачака на површини земље.

Поновљивост

Тригонометрија се не бави само угловима и странама троугла, иако је од тог тренутка почела његова егзистенција. У свим областима где постоји цикличност (биологија, медицина, физика, музика, итд.) Наићи ћете на распоред чије име вероватно знате је синусни талас.

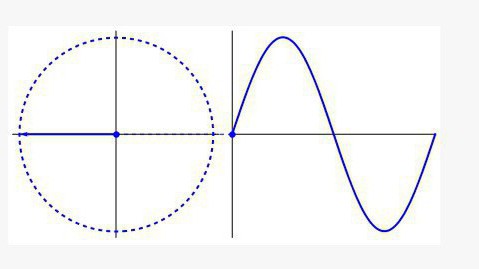Такав граф је круг који се развија по временској оси и изгледа као талас. Ако сте икада радили са осцилоскопом у класи у физици, разумете о чему се ради. И музички еквилајзер и уређај који приказује срчане ритмове користе своје тригонометријске формуле.

У закључку

Размишљајући о томе како научити тригонометрију, већина ученика средњих и средњих школа почиње је сматрати сложеном и непрактичном науком, јер се само упознају са досадним информацијама из уџбеника.

Што се тиче непрактичности - већ смо видели да у различитим степенима, способност да се управља синусима и тангентима је потребна у готово свим областима активности. Што се тиче сложености ... Размислите: ако су људи користили ово знање пре више од две хиљаде година, када је одрасла особа имала мање знања од данашњег средњошколца, да ли је заиста могуће за вас да проучите ову област науке на основном нивоу? Неколико сати пажљивих лекција са решавањем проблема - и ви ћете постићи свој циљ проучавањем основног курса, тзв. Тригонометрије за лутке.