Које су методе оптимизације? Методе оптимизације управљачких одлука

Најприхватљивије рјешење које се доноси на менаџерском нивоу у вези са било којим питањем сматра се оптималним, а процес његове претраге сматра се оптимизацијом.

Међузависност и сложеност организационих, социо-економских, техничких и других аспеката управљања производњом сада је сведена на доношење управљачких одлука које утичу на велики број различитих фактора који су блиско међусобно повезани, што онемогућава анализу сваке од њих појединачно користећи традиционалну аналитичку анализу. методе.

Већина фактора је одлучујућа у процесу доношења одлука и они (у суштини) нису подложни било каквој квантитативној карактеризацији. Постоје и оне које су практично непромењене. С тим у вези, постало је неопходно развити посебне методе које могу осигурати избор важних управљачких одлука у оквиру сложених организационих, економских, техничких задатака (експертске процјене, оперативне истраживачке и оптимизацијске методе, итд.).

Методе за испитивање операција користе се у циљу проналажења оптималних решења у областима управљања као што су организација производних и транспортних процеса, планирање великих размера производња, материјал и техничко снабдевање.

Методе за оптимизацију решења треба проучити упоређивањем нумеричких процена низа фактора, чија се анализа традиционалним методама не може урадити. Оптимално решење је најбоље међу могућим опцијама економски систем а најприхватљивији у односу на поједине елементе система је субоптималан.

Суштина операција истраживачких метода

Као што је раније поменуто, они формирају методе за оптимизацију управљачких одлука. Њихова основа су математички (детерминистички), пробабилистички модели који представљају процес, активност или систем који се истражује. Овакав модел представља квантитативну карактеристику одговарајућег проблема. Они служе као основа за узимање важног управне одлуке у процесу претраживања оптимално прихватљива опција.

Списак питања која играју значајну улогу за директне менаџере производње и који се решавају у току коришћења разматраних метода:

• степен валидности изабраних решења;
• колико су боље од алтернативних;
• степен разматрања детерминантних фактора;
• који је критеријум оптималности одабраних решења.

Ове методе за оптимизацију решења (менаџерски) имају за циљ проналажење оптималних решења за што више предузећа, компанија или њихових подјела. Они се заснивају на постојећим достигнућима статистичких, математичких и економских дисциплина (теорија игара, чекање, графови, оптимално програмирање, математичка статистика).

Методе експертске евалуације

Ове методе оптимизације управљачких одлука примјењују се када је задатак дјелимично или у потпуности не подложан формализацији, а његово рјешење се не може пронаћи математичким методама.

Стручност је проучавање сложених специфичних питања у фази израде специфичне управљачке одлуке од стране релевантних особа које посједују посебну базу знања и импресивно искуство за добијање закључака, препорука, мишљења, евалуација. У процесу стручног истраживања користе се најновија достигнућа науке и технологије као дио специјализације стручњака.

Разматране методе оптимизације низа управљачких одлука (експертске процјене) су ефикасне у рјешавању сљедећих управљачких задатака у сфери производње:

1. Проучавање сложених процеса, феномена, ситуација, система, које карактеришу неформализоване, квалитативне карактеристике.
2. Рангирање и одређивање према задатом критеријуму значајних фактора који су одлучујући за функционисање и развој производног система.
3. Разматране методе оптимизације посебно су ефикасне у области прогнозирања трендова развоја производног система, као и његове интеракције са спољним окружењем.
4. Побољшање поузданости експертских процјена углавном су циљне функције, које су квантитативне и квалитативне природе, усредоточујући ставове квалифицираних стручњака.

Ово су само неке од метода за оптимизацију одређеног броја управљачких одлука (пеер ревиев).

Класификација разматраних метода

Методе за решавање проблема оптимизације, на основу броја параметара, могу се поделити на:

• Методе једнодимензионалне оптимизације.
• Методе оптимизације су вишедимензионалне.

Они се такође називају "нумеричким методама оптимизације". Да будемо прецизнији, то су његови алгоритми претраге.

У оквиру примене деривативних метода су:

• методе директне оптимизације (нулти ред);
• градијентне методе (1. ред);
• методе другог реда, итд.

Већина метода вишедимензионалне оптимизације је блиска проблему друге групе метода (једнодимензионална оптимизација).

Технике униваријатне оптимизације

Било које нумеричке методе оптимизације заснивају се на приближном или тачном прорачуну његових карактеристика, као што су вредности функције циља и функције које дефинишу дозвољени скуп, њихове деривате. Дакле, за сваки појединачни задатак, питање избора карактеристика за прорачун може се ријешити у зависности од постојећих својстава дотичне функције, расположивих могућности и ограничења у складиштењу и обрада информација.

Постоје следећи методи за решавање проблема оптимизације (једнодимензионални):

• Фибонацци метод;
• дихотомије;
• златна секција;
• двоструки корак.

Фибоначијева метода

Прво морате поставити координате т. Кс на интервал [а; б] као број који је једнак односу разлике (к - а) према разлици (б - а). Према томе, а има релативни интервал [а; б] координата 0, и б - 1, средина ½.

Ако претпоставимо да су Ф0 и Ф1 једнаки један другом и да узмемо вредност 1, Ф2 ће бити једнако 2, Ф3 - 3, ..., онда Фн = Фн-1 + Фн-2. Дакле, Фн је Фибоначијеви бројеви, а Фибоначијево претраживање је оптимална стратегија за такозвано секвенцијално максимално претраживање јер је прилично блиско повезана с њима.

У оквиру оптималне стратегије уобичајено је изабрати кн - 1 = Фн - 2: Фн, кн = Фн - 1: Фн. За било који од ова два интервала ([0; кн] или [кн - 1; 1]), од којих сваки може дјеловати као сужени интервал несигурности, точка (наслијеђена) у односу на нови интервал имаће или координате [Фн - 3: Фн– 1] или [Фн-2: Фн-1]. Даље, тачка се узима као кн - 2, која, у односу на нови јаз, има једну од приказаних координата. Ако употребимо Ф (кн - 2), вредност функције, која је наслеђена из претходног јаза, постаје могуће смањити интервал несигурности и пренети наслеђивање једне вредности функције.

На завршном кораку могуће је прећи на такав интервал несигурности као [а; б], док је средина наслеђена из претходног корака. Као к1, постављена је тачка која има релативну координату ½ + ε, а коначни интервал несигурности биће [0, ½ + ε] или [1/2, 1] у односу на [а; б].

На првом кораку, дужина овог интервала је смањена на Фн - 1: Фн (из једног). На завршним корацима редукција дужина одговарајућих интервала је представљена бројевима Фн - 2: Фн - 1, Фн - 3: Фн - 2, ..., Ф2: Ф3, Ф1: Ф2 (1 + 2ε). Дакле, дужина таквог интервала као коначна верзија ће узети вредност (1 + 2ε): Фн.

Ако занемаримо ε, онда асимптотски 1: Фн ће бити једнако рн, са н → ∞, и р = (√5 - 1): 2, што је приближно једнако 0.6180.

Треба напоменути да асимптотски за значајан н сваки наредни корак Фибоначијевог претраживања значајно сужава размотрени интервал са горе наведеним коефицијентом. Овај резултат треба упоредити са 0,5 (коефицијент сужавања интервала несигурности у оквиру методе бисекције како би се пронашла функција нула).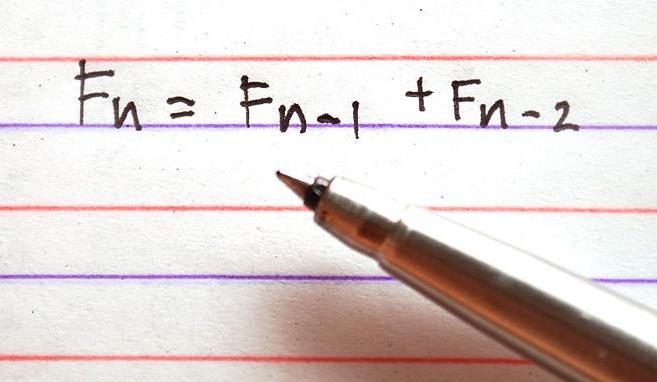

Метод дихотомије

Ако представимо одређену објективну функцију, онда прво морамо наћи њен екстрем у интервалу (а; б). Да би се то постигло, оса апсцисе је подијељена на четири еквивалентна дијела, онда је потребно одредити вриједност дотичне функције на 5 бодова. Затим одаберите минимум међу њима. Екстремум функције мора да лежи унутар интервала (а '; б'), који је суседан минималној тачки. Границе претраге сужене су 2 пута. А ако се минимум налази у м, А или б, онда се сужава четири пута. Нови интервал је подељен на четири једнака сегмента. Због чињенице да су вриједности ове функције у три точке одређене на претходној фази, потребно је израчунати објективну функцију у двије точке.

Метод златне секције

За значајне вредности н, координате тачака као кн и кн - 1 су близу 1 - р, што је једнако 0.3820, а р ≈ 0.6180. Гурање ових вредности је веома близу жељеној оптималној стратегији.

Ако претпоставимо да је Ф (0,3820)> Ф (0,6180), онда је одређен интервал [0; 0,6180]. Међутим, пошто је 0.6180 * 0.6180 ≈ 0.3820 ≈ кн-1, тада је у овој тачки Ф већ познато. Према томе, у свакој фази, почевши од другог, потребан је само један израчун објективне функције, а сваки корак смањује дужину разматраног интервала за фактор 0,6180.

За разлику од Фибоначијевог претраживања, овај метод не захтева фиксирање броја н чак и пре почетка претраге.

"Златна секција" (а; б) секције је део где је однос његове дужине р са већим делом (а; ц) идентичан односу већег дела р на мањи, односно (а; ц) до (ц; б). Није тешко претпоставити да је р одређен горњом формулом. Стога, са значајним н, Фибоначијев метод улази у овај.

Метода дуплирања степена

Суштина је у потрази за правцем смањења циљне функције, кретања у том правцу у случају успешне претраге са постепено растућим кораком.

Прво, одредимо почетну координату М0 функције Ф (М), минималну вредност корака х0, правац претраге. Тада дефинишемо функцију у м. Затим направите корак и пронађите вредност ове функције у овом тренутку.

Ако је функција мања од вриједности која је била на претходном кораку, требате извршити сљедећи корак у истом смјеру, претходно га повећавајући 2 пута. Када је његова вредност већа од претходне, мораћете да промените смер претраге, а затим почнете да се крећете у изабраном правцу кораком х0. Приказани алгоритам се може модификовати.

Методе вишедимензионалне оптимизације

Наведени метод нултог реда не узима у обзир деривате минимизиране функције, тако да њихова употреба може бити ефикасна у случају било каквих потешкоћа с израчунавањем деривата.

Група метода првог реда назива се и градијент, јер се градијент ове функције користи за одређивање правца претраге - вектора чије су компоненте парцијални деривати минимизиране функције у односу на одговарајуће оптимизоване параметре.

У групи метода другог реда користе се 2 деривата (њихова употреба је прилично ограничена због присутности тешкоћа у њиховом израчунавању).

Листа метода безусловне оптимизације

Када се користи вишедимензионално претраживање без употребе деривата, безусловне методе оптимизације су следеће:

• Хоок и Јеевес (реализација 2 типа претраге - на моделу и истраживању);
• минимизирање исправног симплекса (тражење минималне тачке одговарајуће функције упоређивањем на свакој појединачној итерацији њених вредности у врховима симплекса);
• циклични координатни силазак (користећи координатне векторе као референтне тачке);
• Росенброцк (заснован на употреби једнодимензионалног минимизирања);
• минимизирање деформисаним симплексом (модификација методе минимизирања обичним симплексом: додавање процедуре компресије, екстензија).

У ситуацији коришћења деривата у процесу вишедимензионалног претраживања, издваја се метода најбржег спуштања (најосновнија процедура за минимизирање диференцијабилне функције с неколико варијабли).

Они такође разликују такве методе које користе коњугиране правце (Давидон-Флетцхер-Повелл Метход). Његова суштина је приказивање праваца претраге као Дј * град (ф (и)).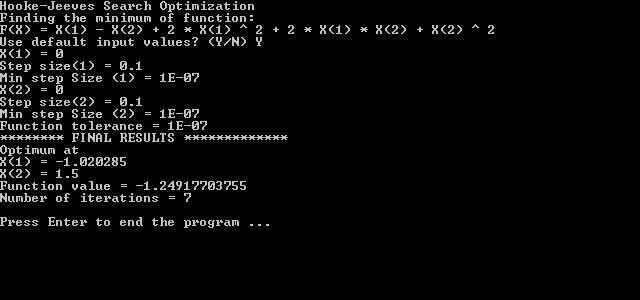

Класификација математичких метода оптимизације

Конвенционално, на основу димензија функција (мета), оне су:

• са 1 варијаблом;
• мултидимензионалан.

У зависности од функције (линеарне или нелинеарне), постоји велики број математичких метода које имају за циљ проналажење екстрема за решавање проблема.

Према критеријуму за коришћење деривата, методе математичке оптимизације се деле на:

• методе за израчунавање 1 деривата објективне функције;
• вишедимензионална (1. деривација - векторска величина - градијент).

На основу ефикасности прорачуна, постоје:

• брзе методе израчунавања екстремитета;
• поједностављено рачунање.

Ово је условна класификација разматраних метода.

Оптимизација пословних процеса

Овде се методе могу користити другачије, у зависности од проблема које треба решити. Уобичајено је издвојити следеће методе за оптимизацију пословних процеса:

• изузеци (смањење постојећих нивоа процеса, елиминација узрока интерференције и контроле улаза, смањење транспортних праваца);
• поједностављења (олакшавање доношења налога, смањење сложености структуре производа, дистрибуција посла);
• стандардизација (употреба посебних програма, метода, технологија, итд.);
• убрзање (паралелно инжењерство, стимулација, оперативни дизајн прототипова, аутоматизација);
• промене (промене у области сировина, технологија, метода рада, локација особља, системи рада, количина наруџбине, поступак обраде);
• обезбеђивање интероперабилности (у смислу организационих јединица, особља, система рада);
• селекцију и инклузију (у вези са неопходним процесима, компонентама).

Пореска оптимизација: методе

Руско законодавство пружа пореским обвезницима веома богате могућности за смањење износа пореза, због чега је уобичајено да се издвоје методе којима се оне минимизирају, као што су опште (класичне) и специјалне.

Опште методе оптимизације пореза су следеће:

• израда рачуноводствене политике компаније уз максимално коришћење могућности које пружа руско законодавство (поступак отписа ИБЕ, избор начина обрачуна прихода од продаје робе, итд.);
• оптимизација путем уговора (закључење повлашћених трансакција, јасна и компетентна употреба текста итд.);
• коришћење различитих врста накнада, пореских ослобођења.

Другу групу метода могу користити и све фирме, али оне још увијек имају прилично уски опсег. Посебне методе оптимизације пореза су:

• замјена односа (операција, која предвиђа оптерећујуће опорезивање, замјењује се другом, што вам омогућава постизање сличног циља, али у исто вријеме и преференцијалног опорезивања).
• раздвајање односа (замјена само дијела пословне трансакције);
• одлагање плаћања пореза (одлагање тренутка настанка) пореска ставка за други календарски период);
• директно смањење предмета опорезивања (ослобађање од многих опорезивих трансакција или имовине без негативног утицаја на главну економску активност предузећа).