Који је тренутак измјерене инерције, које је његово физичко значење?

Ротација механичког система је један од најчешћих начина кретања тела у простору. Овај тип кретања карактерише скуп физичких величина, чије име садржи реч "тренутак". Овај чланак је посвећен одговору на следеће питање: у ком тренутку се мери момент инерције?

Карактеристика ротације

Сви су свесни шта је у питању. Довољно је споменути ротацију точкова аутомобила, бицикла или котача у забавном парку. Ако говоримо о великим просторима и масама, онда можемо да се сетимо ротације наше Земље око звезде Сунца.

У физици, сва померања објеката уочена у горњим примерима обично се описују следећом једначином:

М¯ = дЛ¯ / дт.

Овдје је М тренутак вањске силе, која, дјелујући на систем за вријеме дт, узрокује промјену кутног момента за вриједност дЛ. Трака изнад знакова означава да су то вектори.

Ако спољашње силе немају никакав моменат М¯, онда горња једнаџба постаје такозвани закон очувања момента момента Л¯, односно:

Л¯ = цонст.

Кутни моменат (који се назива и кутни момент) уноси се у физику као векторски производ линеарног момента тачке са масом м и брзине в¯ и вектора р¯, који је окомит на ос ротације и повезује га са овом тачком, односно:

Л¯ = р¯ * м * в¯.

Ако употребимо концепт угаоне брзине ω¯ и њену везу са сличном линеарном величином в, онда се ова једнакост може поново написати у овом облику:

Л¯ = И * ω¯.

У овом изразу, И је фактор који повезује две векторске величине. Добио је име тренутка инерције.

Магнитуда у физици

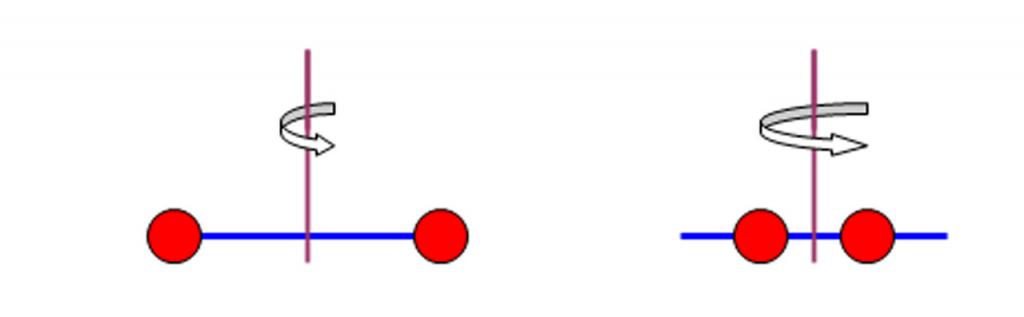
У последњем изразу претходног параграфа, вредност И је једнака производу масе тачке квадратом њене удаљености од осе, односно:

И = м * р ² .

Пошто сва реална тела нису материјалне тачке, већ имају одређене просторне параметре и облик, да би се одредио њихов моменат инерције, користи се оригинални горе наведени израз, који постаје интегранд. Општа формула за тело И је следећа:

И = ( _м (р ² * дм).

Ова математичка формула каже да је, да би се израчунао тренутак инерције целог тела, потребно ментално поделити у материјалне тачке дм, помножити их квадратом растојања до осе ротације, а затим додати све резултате.

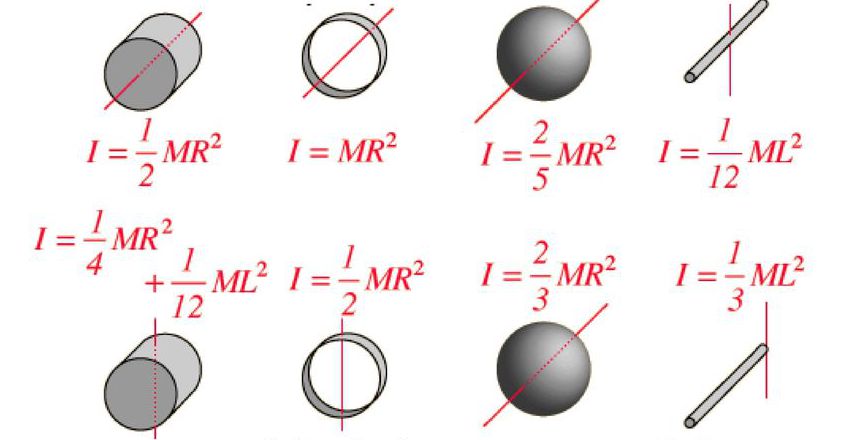
Како се мери момент инерције тела?

Будући да је горе наведено основна информација коју морате знати да бисте разумјели вриједност о којој се ради, сватко може одговорити на питање ове ставке. Ипак, разматрамо га детаљније.

Дакле, у којим јединицама се мери момент инерције тела? И формула за материјалну тачку и општи израз за тело произвољног облика воде до истог одговора: вредност И апсолутно било ког ротационог система се мери у килограмима по квадратном метру (кг * м ² ).

Наравно, да би се изразио момент инерције, можете користити било које фракционе јединице из наведеног стандарда у СИ. На пример, за системе са малим масама и линеарним димензијама, И се може изразити у грамима по центиметру на квадрат (г * цм2). Насупрот томе, мегатони се могу користити на космичким скалама за астрономске јединице у квадрату (најчешће се ипак користи кг * м ² са бројем 10, изграђеним у великој мјери).

Одговарајући на питање како се мјери тренутак инерције, треба споменути другачији приступ како би се изразила та количина. Да бисмо га разумели, напишите формулу за промену момента момента:

М¯ = дЛ¯ / дт = И * дω¯ / дт, дакле, И = М¯ * дт / дω¯.

Пошто се моменат сила мери у невтонима по метру (Н * м), дт - у секундама, дω¯ - у радијанима у секунди, добијамо за И:

И = [Н * м * с ² / рад] или [Ј * с ² / рад].

Обе јединице мерења су истините за И, али готово да се не користе у решавању проблема, јер су изведене из стандарда у СИ, тј. Од кг * м ² . Ипак, ове јединице (посебно потоње) повезане су са физичким значењем процеса ротације тела.

Значење ја

Узимајући у обзир питање јединица у којима се мери момент инерције, можемо рећи и шта то значи.

Ако обратимо пажњу на облик снимања момента Л¯ кроз брзину ω¯, онда можемо приметити њену потпуну сличност са изразом за линеарни импулс. Из ове сличности следи да је момент инерције И нека врста масе за кретање ротације. Што више ја, то је теже убрзати систем (окретати га или га заустављати).

С обзиром на физичко значење И са становишта енергије, окренимо се јединици мере која је добијена у претходном параграфу - [Ј * с ² / рад]. Показује се да је за момент инерције тела при 1 Ј * с ² / рад (1 кг * м ² ) неопходно да тренутак сила ради на 1 Ј да би се систему дало угажно убрзање једнако 1 рад / с2.

Секција момента инерције

Одговарајући на питање како се мери момент инерције, разматрали смо вредност И за ротирајуће тело. Ипак, постоји још једна количина, која се у математици назива моментом инерције другог реда. Ово је сасвим другачија вредност од разматране. Израчунава се преко двоструког интеграла за произвољан попречни пресјек и користи се за анализу напона савијања који настају у стварним тијелима када су изложени вањским оптерећењима. Овај момент инерције се мери у јединицама дужине до четврте снаге, односно у м ⁴ .