Основни појмови теорије вјероватноће и математичке статистике

Математика обухвата читав низ области, од којих је једна, поред алгебре и геометрије, теорија вероватноће. Постоје термини који су заједнички за све ове области, али, поред њих, постоје и специфични, својствени само једној одређеној „ниши“ речи, формуле, теореме.

Фраза "теорија вероватноће" изазива панику код неспремног ученика. Заиста, машта слика слике, где се појављују страшне волуметријске формуле, а решење једног проблема заузима читаву бележницу. Међутим, у пракси ствари уопште нису тако страшне: довољно је једном схватити значење неких појмова и доћи до сржи неке чудне логике расуђивања како би се престало бојати задатака једном за свагда. У том смислу разматрамо основне концепте теорије вероватноће и математичке статистике - младо, али изузетно интересантно поље знања.

Зашто учити појмове

Функција језика је да пренесе информације од једне особе до друге, тако да је разуме, оствари и може да је користи. Сваки математички концепт може се објаснити једноставним ријечима, али у овом случају за размјену података потребно је много више времена. Замислите да уместо речи "хипотенуза" увек треба да кажете "најдужа страна правог троугла" - ово је изузетно незгодно и дуго.

Зато људи измишљају нове термине за одређене појаве и процесе. Основни концепти теорије вероватноће - догађај, вероватноћа догађаја, итд. - појавили су се на исти начин. Дакле, да би користили формуле, решавали проблеме и примењивали вештине у животу, потребно је не само да запамтите нове речи, већ и да разумете шта свако од њих значи. Што их дубље постанете свјесни, уђите у значење, шири опсег ваших могућности постаје, и што потпуније перципирате свијет око себе.

Какво је значење субјекта

Упознаћемо се са основним концептима теорије вјероватноће. Класична дефиниција вероватноће је следећа: ово је однос исхода који одговара истраживачу укупном броју могућих. Хајде да наведемо једноставан пример: када особа окрене коцку, може да спусти било коју од шест страна нагоре. Дакле, укупан број исхода је шест. Вјероватноћа насумично одабраног испадања стране је 1/6.

Способност предвиђања настанка одређеног резултата изузетно је важна за различите специјалисте. Колико се неисправних дијелова очекује у великој мјери? То зависи од тога колико да се произведе. Која је вероватноћа да ће медицина помоћи у борби против болести? Такве информације су од виталног значаја. Али не губимо време на додатне примере и наставимо да проучавамо нову област за нас.

Прво познанство

Размотримо основне концепте теорије вероватноће и њихову употребу. Ин ригхт натурал науке, економске формуле и термини приказани у наставку се користе свуда, јер су директно повезани са статистиком и грешкама мерења. Детаљнија студија овог питања ће вам отворити нове формуле које су корисне за прецизније и сложеније калкулације, али почнимо са једноставном.

Један од најосновнијих и основних принципа теорије вероватноће и математичке статистике је случајан догађај. Објасните јасним речима: од свих могућих исхода експеримента, само један се посматра као резултат. Чак и ако је вероватноћа појаве овог догађаја много већа од друге, то ће бити случајно, јер је теоретски резултат могао бити различит.

Ако смо спровели низ експеримената и добили одређени број исхода, онда се вероватноћа сваког од њих израчунава помоћу формуле: П (А) = м / н. Овде, м је колико пута у тест серији смо видели резултат од интереса за нас. Заузврат, н је укупан број изведених експеримената. Ако смо 10 пута бацили новчић и добили 5 "репова", онда је м = 5, а н = 10.

Врсте догађаја

Дешава се да се неки исход гарантује да ће се посматрати у сваком суђењу - такав догађај ће се назвати поузданим. Ако се никада не догоди, то ће се звати немогуће. Међутим, такви догађаји се не користе у условима проблема на теорији вероватноће. Основни појмови који су много важнији јесу заједнички и некомпатибилни догађаји.

Дешава се да се током експеримента истовремено дешавају два догађаја. На пример, бацамо две коцкице - у овом случају, чињеница да је неко имао “шест” није гарантовао да други неће пасти на други. Такви догађаји ће се звати заједнички.

Ако умотамо једну, онда два броја у исто време неће моћи да испадну. У овом случају, исходи у облику испуштених “један”, “два”, итд. Ће се сматрати некомпатибилним догађајима. Веома је важно разликовати који се исходи дешавају у сваком конкретном случају - зависи од које формуле да се користи у проблему проналажења вероватноће. Основни концепти теорије вероватноће, наставићемо да проучавамо неколико параграфа касније, када узмемо у обзир карактеристике збрајања и множења. Заиста, без њих се не може решити никакав проблем.

Количина и производ

Претпоставимо да окренете умријети с пријатељем, а он има “четири”. Треба да добијеш пет или шест да победиш. У овом случају, вероватноће ће бити сабране: будући да су изгледи за одустајање оба броја 1/6, одговор ће изгледати 1/6 + 1/6 = 1/3.

Сада замислите да двапут окренете коцку и ваш пријатељ има 11 поена. Сада требате имати шест пута два пута заредом. Догађаји су међусобно независни, па се вјероватноћа мора умножити: 1/6 * 1/6 = 1/36.

Међу основним појмовима и теоремама теорије вјероватноће треба обратити пажњу на суму вјероватноћа заједничких догађаја, т. то јест, оне које се могу појавити истовремено. Формула у овом случају ће изгледати овако: П (А + Б) = П (А) + П (Б) - П (АБ).

Комбинаторика

Врло често морамо пронаћи све могуће комбинације неких параметара објекта или израчунати број било које комбинације (на примјер, при одабиру шифре). Комбинаторика, која је уско повезана са теоријом вјероватноће, помоћи ће нам у томе. Основни концепти овде укључују неке нове речи, а одређени број формула из ове теме ће свакако бити од користи.

Претпоставимо да имате три броја: 1, 2, 3. Потребно је, користећи их, написати све могуће трознаменкасте бројеве. Колико ће их бити? Одговор: н! (ускличник меанс фацториал). Комбинације више различитих елемената (бројеви, слова, итд.), Које се разликују само по редоследу њихове локације, називају се пермутације.

Међутим, чешће се сусрећемо са таквом ситуацијом: постоји 10 цифара (од нула до девет), од којих је састављена лозинка или код. Претпоставимо да је његова дужина 4 знака. Како израчунати укупан број могућих кодова? За то постоји посебна формула: (н!) / (Н - м)!

С обзиром на предложени проблемски проблем, н = 10, м = 4. Даље, потребна су само једноставна математичка израчунавања. Иначе, такве комбинације ће се звати пласман.

Коначно, ту је и концепт комбинација - то су секвенце које се међусобно разликују најмање једним елементом. Њихов број се израчунава по формули: (н!) / (М! (Нм)!).

Математичка очекивања

Важан концепт који ученик сусреће већ у првим разредима на предмету је математичко очекивање. То је збир свих могућих вредности резултата помножених са њиховим вероватноћама. У суштини, ово је просечан број који можемо предвидети као резултат теста. На пример, постоје три вредности за које су вероватноће приказане у заградама: 0 (0,2); 1 (0.5); 2 (0.3). Израчунајте очекивање: М (Кс) = 0 * 0.2 + 1 * 0.5 + 2 * 0.3 = 1.1. Дакле, из предложеног израза можемо видети да је ова вредност константна и да не зависи од исхода теста.

Овај концепт се користи у многим формулама, а ви ћете га у будућности више пута наићи. Лако је радити с њим: очекивање суме је једнако зброју тепиха. очекивања - М (Кс + И) = М (Кс) + М (И). Исто важи и за производ: М (КСИ) = М (Кс) * М (И).

Дисперзија

Мора да је то из школског курса физике, да се сећате да се дисперзија расипа. Које је њено место међу основним концептима теорије вероватноће?

Погледајте два примера. У једном случају дат је: 10 (0,2); 20 (0,6); 30 (0,2). У другом - 0 (0,2); 20 (0,6); 40 (0,2). Математичка очекивања у оба случаја ће бити иста, па како можемо да упоредимо ове ситуације? На крају крајева, голим оком видимо да је ширење вриједности у другом случају много веће.

У ту сврху уведен је концепт дисперзије. Да бисте га добили, морате израчунати очекивање сума разлика сваке случајне варијабле и очекивања. Узмите бројеве из првог примера забележеног у претходном пасусу.

Прво, израчунамо очекивање: М (Кс) = 10 * 0.2 + 20 * 0.6 + 30 * 0.2 = 20. Онда вредност варијансе: Д (Кс) = 40.

Још један од основних концепата статистике и теорије вероватноће је стандардна девијација. Израчунајте је врло једноставно: само требате узети скуаре роот из дисперзије.

Овде можемо навести тако једноставан израз, као обим. Ова вредност показује разлику између максималне и минималне вредности у узорку.

Статистика

Неки основни школски концепти се често користе у науци. Два су аритметичка средина и медијана. Сигурно се сјећате како пронаћи њихове вриједности. Али за сваки случај, присјетимо се: аритметички просјек је зброј свих вриједности подијељених њиховим бројем. Ако је вредност 10, онда их додамо и поделимо за 10.

Средина је централна за све могуће. Ако имамо непаран број вредности, онда их запишемо у растућем редоследу и изаберемо онај који је био у средини. Ако имамо паран број вредности, узмемо два централна и поделимо на два.

Још две вредности, које се налазе између медијана и две екстремне вредности - максимум и минимум - вредности скупа, називају се квартили. Оне се рачунају на исти начин - са непарним бројем елемената узима се број који се налази у средини реда, а за парну - половину сума два централна елемента.

Ту је и посебан графикон у којем можете видјети све вриједности узорка, његов опсег, медијан, интер-четврт интервал, као и оутлиерс - вриједности које се не уклапају у статистичку погрешку. Добијена слика има врло специфично (па чак и не-математичко) име - кутију са брковима.

Дистрибуција

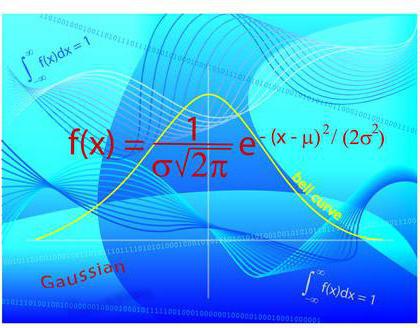
Дистрибуција се такође односи на основне појмове теорије вероватноће и математичке статистике. Укратко, то је сажетак свих случајних варијабли које можемо видјети као резултат теста. Главни параметар овде је вероватноћа појаве сваке специфичне вредности.

Нормална дистрибуција је она која има један централни врх, у којем се налази вредност која се најчешће јавља. Из ње се лукови разликују све мање и мање вјероватно. Генерално гледано, распоред са стране изгледа као „слајд“. У будућности ћете научити да је централна гранична теорема, која је фундаментална за теорију вероватноће, уско повезана са овом врстом дистрибуције. Описују се закони који су важни за гране математике које разматрамо, а које су веома корисне за разне калкулације.

Али вратимо се на тему. Постоје још два типа дистрибуције: асиметрична и мултимодална. Прва изгледа као половина "нормалног" графикона, тј. Лук иде само у једном смеру од вршне вредности. Коначно, мултимодална дистрибуција је она која има неколико “горњих” вредности. Распоред, дакле, пада, затим расте. Највише фреквенција у било којој дистрибуцији се назива мод. То је такође један од основних појмова теорије вероватноће и математичке статистике.

Гауссова дистрибуција

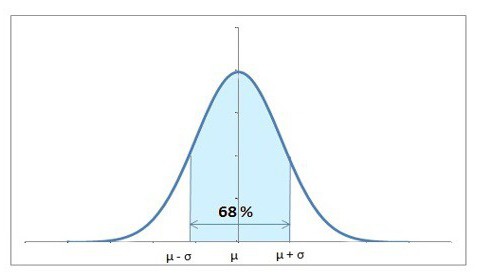
Гаусова, или нормална, расподјела је она у којој одступање од опажања из средње вриједности поштује одређени закон.

Укратко, главно расипање вредности узорка експоненцијално тежи моду - најчешћем од њих. Да говоримо прецизније, онда 99,6% свих вредности лежи у оквиру три стандардне девијације (запамтите, ми смо погледали овај концепт изнад?).

Гаусова дистрибуција је један од основних појмова теорије вероватноће. Уз то, могуће је схватити да ли је неки елемент укључен у категорију „типичног“ према једном или другом параметру - то је како се висина и тежина особе процјењује према старости, нивоу интелектуалног развоја, психолошком стању и још много тога.

Како се пријавити

Занимљиво је да се “досадни” математички подаци могу искористити у своју корист. На пример, један младић применио је теорију вероватноће и статистику да би у рулету добио неколико милиона долара. Истина, морали смо се припремити за то - током неколико мјесеци смо забиљежили резултате игара у разним коцкарницама.

Након анализе, открио је да је једна од табела благо нагнута, што значи да се број вриједности појављује статистички значајно чешће од других. Мало калкулације, стрпљења - а сада су власници установе збуњени, размишљајући како особа може бити тако сретна.

Постоји много свакодневних свакодневних задатака који се не могу ријешити без употребе статистике. На пример, како одредити колико продавница можете наручити у различитим величинама: С, М, Л, КСЛ? Да би се то урадило, потребно је анализирати ко често купује одећу у граду, на том подручју, у оближњим продавницама. Ако се такве информације не добију, власник ризикује да изгуби много новца.

Закључак

Размотрили смо читав низ основних појмова теорије вероватноће: тест, догађај, пермутације и пласмани, очекивање и варијанца, мод и нормална дистрибуција ... Поред тога, испитали смо и низ формула које су више од једног месеца истраживања биле посвећене проучавању којих.

Не заборавите: математика је неопходна за учење економије, природних наука, информатике, инжењерских специјалности. Статистике као једну од својих области овде се такође не могу избећи.

Сада је на вама: вежбајте, решавајте проблеме и примере. Чак ће и основни појмови и дефиниције теорије вјероватноће бити заборављени, ако не и посвећивање времена понављању. Поред тога, следеће формуле ће се у великој мери ослањати на оне које смо размотрили. Зато их покушајте запамтити, поготово зато што их нема много.