Децималне фракције и акције са њима. Децимална подела и множење

Децимална фракција се користи када је потребно извршити радње са не-бројевима. Ово може изгледати ирационално. Али ова врста бројева увелико олакшава математичке операције које се морају обавити с њима. Ово разумевање долази с временом, када им се запис сазнаје, а читање не изазива потешкоће, а правила за децималне фракције се савладавају. Штавише, све акције понављају већ познате, од којих се учи природни бројеви. Само треба да запамтите неке карактеристике.

Дефиниција децималне фракције

Децимална фракција је специјални приказ не-целог броја са имениоцем који је дељив са 10, а одговор се добија као јединица и, евентуално, са нулама. Другим речима, ако је именилац 10, 100, 1000, и тако даље, онда је згодније да се број преписује помоћу зареза. Онда це се цео део налазити пре њега, а затим и фракцијски део. Штавише, снимање друге половине броја ће зависити од имениоца. Број цифара, које су у фракцијском делу, треба да буде једнак рангу имениоца.

Ово можете илустровати овим бројевима:

9/10 = 0.9; 178/10000 = 0,0178; 3.05; 56 003,7006.

Разлози за употребу децималних фракција

Математичари су узимали децималне фракције из неколико разлога:

1. Поједноставите снимање. Таква фракција се налази дуж једне линије без цртице између имениоца и нумератора, док видљивост не трпи.

2. Једноставност у поређењу. Довољно је само повезати бројеве на истим позицијама, док би са обичним фракцијама морали да их доведете у заједнички именитељ.

3. Поједноставите калкулације.

4. Калкулатори нису дизајнирани за увођење обичних фракција, они користе децимални запис за све операције.

Како читати такве бројеве?

Одговор је једноставан: баш као и обични мјешовити број са деноминатором вишеструким од 10. Једини изузетак су фракције без целих вредности, онда када читате морате изговорити “нула целих бројева”.

На пример, 45/1000 треба изговорити као четрдесет пет хиљадитих , док ће 0.045 звучати као нулта тачка четрдесет пет хиљада .

Мјешовити број са целим бројем једнак 7 и фракцијом 17/100, који је написан као 7.17, у оба случаја ће се читати као седам тачака седамнаест стотина .

Улога пражњења у фракцијама

Истина је да се означи отпуст - то је оно што захтијева математику. Децималне фракције и њихова вредност се могу значајно променити ако број напишете на погрешном месту. Међутим, раније је то било истина.

Да бисте прочитали цифре целог броја децималног броја, само требате користити правила позната за природне бројеве. А на десној страни они се огледају и читају другачије. Ако је у читавом делу звучало "десетине", онда ће након зареза већ бити "десетине".

Јасно је да се ово може видјети у овој табели.

Како написати мјешовити број у децималном?

Ако је именитељ број једнак 10 или 100, а други, онда је питање како претворити фракцију у децималну, једноставно. Да би се то урадило, довољно је да се сви његови саставни делови поново напишу на другачији начин. То ће помоћи овим тачкама:

• Мало по страни да напише нумератор фракције, у овом тренутку десна је десна, после последње цифре;

• померајте зарез у лево, најважнија ствар овде је да исправно бројите бројеве - морате да га преместите у онолико позиција колико има нула у имениоцу;

• ако недостају, онда празне позиције треба да буду нуле;

• нуле које су биле на крају нумератора више нису потребне и могу бити прецртане;

• Пре зареза за атрибут целог дела, ако није, онда ће бити и нула.

Пажња. Не можете прекрижити нуле, које су биле окружене другим бројевима.

Како бити у ситуацији када број у именитељу није само из једног и нула, како претворити фракцију у децималну, можете прочитати нешто ниже. Ово је важна информација коју свакако треба да прочитате.

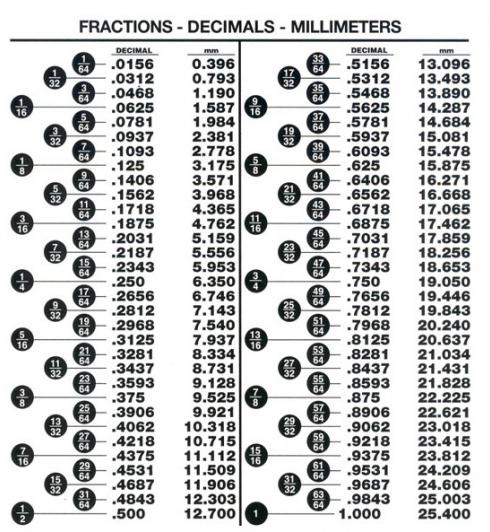
Како претворити дјелић у децимални, ако је именитељ произвољан број?

Овде постоје две опције:

1. Када се именилац може представити као број, који је десет на било који степен.

2. Ако се таква операција не може обавити.

Како то провјерити? Потребно је проширити именитељ на факторе. Ако су само 2 и 5 присутне у производу, онда је све добро, а фракција се лако може претворити у коначну децималу. У супротном, ако се појаве 3, 7 и други прости бројеви онда ће резултат бити бескрајан. Таква децимална фракција за једноставну употребу у математичким операцијама се обично заокружује. Ово ће бити објашњено у наставку.

Проучава како се добијају такве децималне фракције, разред 5. Примери ће бити веома корисни.

Нека су деноминатори бројеви: 40, 24 и 75. Декомпозиција на основне факторе за њих ће бити:

• 40 = 2 · 2 · 2 · 5;
• 24 = 2 · 2 · 2 · 3;
• 75 = 5 · 5 · 3.

У овим примерима, само прва фракција може бити представљена као коначна.

Алгоритам за претварање обичног дијела у коначну децималу

• Проверите ширење имениоца у основне факторе и уверите се да ће се састојати од 2 и 5.

• Додајте овим бројевима чак 2 и 5, тако да постану једнак број. Они ће дати вриједност додатног фактора.

• Да помножимо именитељ и бројник овим бројем. Резултат је обична фракција, испод које је до неке границе 10.

• Наставите да делујете као што је описано у параграфу, који се налази мало више.

Ако се у задатку ове радње изводе са мијешаним бројем, онда се прво мора представити као погрешна фракција. И тек тада поступити по описаном сценарију.

Репрезентација заједничке фракције у облику заобљене децималне

Овај начин како претворити дјелић у децимални ће некоме изгледати још лакше. Зато што нема велики број акција. Потребно је само поделити вредност нумератора са имениоцем.

За било који број са децималним делом десно од зареза, можете доделити бесконачан број нула. Ово својство и потребно је користити.

Прво напишите цијели дио и ставите зарез након њега. Ако је фракција тачна, онда напишите нулу.

Тада је неопходно поделити бројник имениоцем. Тако да је број цифара исти. То јест, додајте потребан број нула десно од нумератора.

Перформ подела по бару до потребног броја цифара. На пример, ако треба да се заокружите на стотинке, онда би требало да буде 3 у одговору.Уопштено, требало би да буде још једна цифра него што је потребно да добијете на крају.

Забиљежите средњи одговор након зареза и заокружите га према правилима. Ако је последња цифра од 0 до 4, онда само треба да је испустите. А када је једнак 5-9, онда се онај пре њега мора повећати за један, одбацујући други.

Повратак из децималног дела у обични

У математици постоје проблеми када су децималне фракције прикладније представљене као обичне, у којима постоји нумератор са имениоцем. Можете да одахнете од олакшања: ова операција је увек могућа.

За овај поступак, урадите следеће:

• напишите целобројни део, ако је нула, онда не морате ништа да пишете;

• нацртај линију;

• изнад њега уписују се бројеви са десне стране, ако су прве нуле, онда их треба прецртати;

• испод линије напишите јединицу са толико нула као број цифара након децималне тачке у почетној фракцији.

Ово је све што треба да урадите да бисте конвертовали децимални део у обични.

Шта се може урадити са децималним фракцијама?

У математици, то ће бити одређене радње са децималним фракцијама које су претходно изведене за друге бројеве.

Они су:

• поређење;

• збрајање и одузимање;

• умножавање и подела.

Прва акција, поређење, слично је начину на који је то учињено за природне бројеве. Да би се утврдило која је већа, мора се упоредити са пражњењем цијелог дијела. Ако се испостави да су једнаки, онда прелазе на делове и поредбе их по реду. Тај број на којем ће бити велика фигура у вишој категорији, такође ће бити одговор.

Додавање и одузимање децималних фракција

Ово је можда најједноставнија акција. Зато што прате правила за природне бројеве.

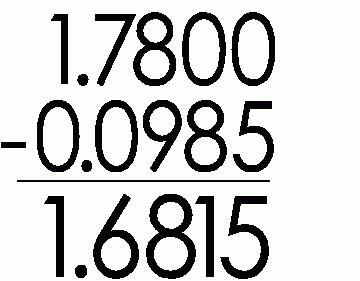
Дакле, да бисте извршили додавање децималних фракција, они морају бити написани један за другим, стављајући зарезе у колону. Са таквим уносом у лево од зареза постоје цели делови, а са десне стране - фракцијски. А сада морате додати бројеве један по један, као што је то учињено са природним бројевима, одбацујући зарез. Неопходно је почети додавање из најмање категорије фракцијског дијела броја. Ако десна половина нема довољно бројева, додајте нуле.

Када се одузме, поступите исто. И овде је правило које описује способност да се узме јединица са вишег нивоа. Ако децимална фракција има мање цифара од дедуцтибле, онда су јој нуле једноставно додијељене.

Мало компликованији је случај са задацима где је потребно извршити умножавање и дељење децималних фракција.

Како множити децимални дио у различитим примјерима?

Правило којим се врши множење децималних фракција природним бројем је:

• упиши их у колону, не обраћајући пажњу на зарез;

• умножите се као да су природне;

• одвојене зарезе са онолико цифара колико их је било у фракцијском делу оригиналног броја.

Посебан случај је примјер у којем је природни број 10 у било којем ступњу. Затим, да бисте добили одговор, само требате помакнути зарез у десну страну у онолико позиција колико има нула у другом множитељу. Другим речима, када се помножи са 10, зарез се помера за једну цифру, за 100 - биће их два, и тако даље. Ако у фракцијском делу нема довољно цифара, онда морате да пишете нуле на празне позиције.

Правило које се користи када у задатку требате помножити децималне фракције с другим истим бројем:

• запишите их један поред другог, не обраћајући пажњу на зарезе;

• умножите се као да су природне;

• одвојене зарезе са онолико цифара колико их је било у делимичним деловима обе оригиналне фракције заједно.

Посебан случај су примјери у којима је један од фактора једнак 0,1 или 0,01 и више. Потребно је да помера зарез у лево од броја цифара у приказаним мултипликаторима. То јест, ако се множи са 0.1, онда се зарез помера за једну позицију.

Како поделити децимални у различитим задацима?

Подела децималних фракција у природни број врши се према следећем правилу:

• напишите их за поделу у бар, као да су природне;

• поделити у складу са уобичајеним правилом док се не заврши цијели дио;

• ставите зарез у одговор;

• настави са дељењем фракционе компоненте док се не добије нула у остатку;

• ако је потребно, можете доделити потребан број нула.

Ако је целобројни део нула, онда то неће бити ни у одговору.

Одвојено, постоји подела на бројеве једнаке десет, стотину и тако даље. У таквим задацима треба да померите зарез у лево од броја нула у делиоцу. Дешава се да у целом делу нема довољно цифара, онда се користе нуле. Видите да је ова операција слична множењу са 0.1 и бројевима сличним томе.

Да бисте извршили децималне фракције, морате да користите ово правило:

• окрените делитељ у природни број, и за то померите зарез у њему десно до краја;

• померање зареза и дивиденде са истим бројем цифара;

• поступати по претходном сценарију.

Издвојите се подела са 0.1; 0.01 и друге сличне бројеве. У таквим примерима, зарез се помера на десно за број цифара у фракцијском делу. Ако су готови, онда треба да додате број који недостаје. Вреди напоменути да ова акција понавља поделу на 10 и сличне бројеве.

Закључак: све је у пракси

Ништа у школи не долази лако и без напора. За поуздани развој новог материјала потребно је време и обука. Математика није изузетак.

Тако да тема децималних фракција не изазива потешкоће, потребно је да решите примере са њима што је више могуће. На крају крајева, дошло је вријеме када је додавање природних бројева збуњено. И сада је све у реду.

Дакле, парафразирати добро познату фразу: одлучити, одлучити и поново ријешити. Тада ће се задаци са таквим бројевима одвијати лако и природно, као друга загонетка.

Иначе, загонетке су у почетку тешко ријешити, а онда морате направити познате покрете. Исто је и код математичких примјера: након што смо неколико пута ишли једним путем, више нећете размишљати о томе гдје да се окренете.