Децимално заокруживање: учење математике

Дакле, сада ћемо видети како се десава децимално заокруживање. У ствари, овај процес није компликован као што се на први поглед чини. Истина, неки ученици имају потешкоћа са овом темом. Помозимо им да разумију наше данашње питање.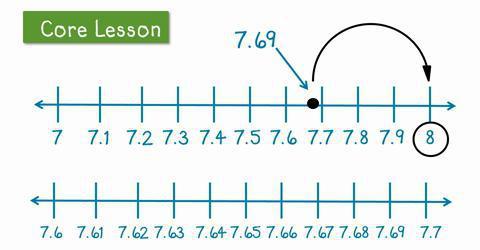

Појам децималне фракције

Пре заокруживања децимале, морамо јасно да разумемо са чиме имамо посла. Што боље разумемо ово питање са вама, то ће бити лакше у будућности.

Уопштено, концепт "децималне фракције" открива се у 5. разреду школе. Ово је врста броја, која се састоји од целог дела и фракцијског, чији је именилац 10.

Да бисмо јасно разумели шта је у питању, погледајмо један пример, а затим испитамо како долази до заокруживања децимала. Овај тип записа ће изгледати овако: 5,26852. Ако преведете добијени број у фракцију, можете видети следеће: 526852/100000. Децималне фракције могу бити и позитивне и негативне. То је све. Сада идемо с вама на наш проблем.

У деловима

Поента је да се заокруживање децималних фракција (Граде 6), по правилу, дешава у деловима. Прво, они заузимају остатак ("реп"), то јест, оне бројеве који су иза зареза. Тек тада се може узети за цео дио.

Прво што се од нас тражи је да одредимо тачност којом ћемо заокружити децималне фракције. До десетина, стотинки, хиљадити део итд. Затим морате слиједити нека правила, као и научити једну важну точку која ће вам свакако помоћи да се носите са задатком. Хајде да радимо са вама са јасним примером. Узмите произвољан број: 78,9563245. На њему ћемо тестирати правило за заокруживање децимала. Сада га упознајемо.

Главно правило

Основни принцип који требамо научити је како замијенити бројеве приликом заокруживања. Ствар је у томе да је прилично лако. Да видимо како.

Ако имате 0, 1, 2, 3 или 4 као цифру, он се аутоматски замењује са 0 и одбацује. Затим, приближите се целом делу и погледајте следећи број.

Чим цифра у цифри буде 5, 6, 7, 8 или 9, морат ћете одбацити овај дио и додати један сљедећем (најближи цијелом дијелу). Овај процес се мора поновити до изабране тачности заокруживања. Погледајмо сада пример са вама. На њему ће све изгледати јасније.

Пример

Дакле, почињемо да заокружујемо децимале са вама. Радимо са бројем 78,9563245. Заокружујемо га до десетог, стотог и хиљадитог. Покушајмо.

За почетак, одбацујемо цијели дио. Добијамо 0.9563245. Наставићемо да радимо са вама са овим бројем. Почињемо заокруживати са хиљадитима, постепено повећавајући тачност.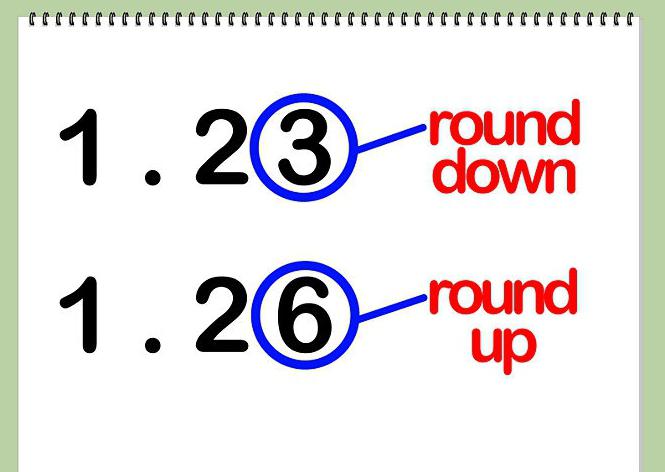

Број је 0.9563245. Креће се ка нули. Први број са краја је 5. То значи да га “конвертујемо” у 0, и додамо 4 до 4. Друга цифра - 4 + 1 = 5. Дакле, додељујемо јединицу следећем знаку, а ова се конвертује у 0.

До сада смо радили са вама: 0.95632 ⁽⁺¹⁾ . Заокруживање на хиљадити је 3 цифре. Хајде да наставимо да радимо са вама. 2 + 1 = 3. Ова цифра је мања од 5с. Дакле, само га замените са 0 и уклоните. Следећа фаза је 3-ка. Ништа му се не додаје. Замените са 0, пошто је мање од 5. Урадили смо то са вама: 0.956. Сада можете да додате цео део: 78,956.

Али наше заокруживање децималних фракција се не завршава. Сада га треба држати до стотине. Да бисмо то урадили, као и раније, погледамо последњу цифру после зареза - 6. Према правилу, замењујемо је са 0, а затим једноставно додамо 1 на цифру лево од ње. Заокруживање на десетину овде није баш погодно. Добили смо цео број са вама. Уосталом, 6-ка ће бити замењена са 0, јединица ће бити додата на 9, а на крају ћемо добити: 78.9 ⁽⁺¹⁾ . То ће бити 79. То је све. Сада знате како обилазити фракције.